有了高效的散列表，为什么还需要二叉树

Posted 2021-01-28 hanguocai

一：二叉查找树可以高效的实现查找，插入删除的操作，这些map也可以实现。那么二叉查找树有什么优势？

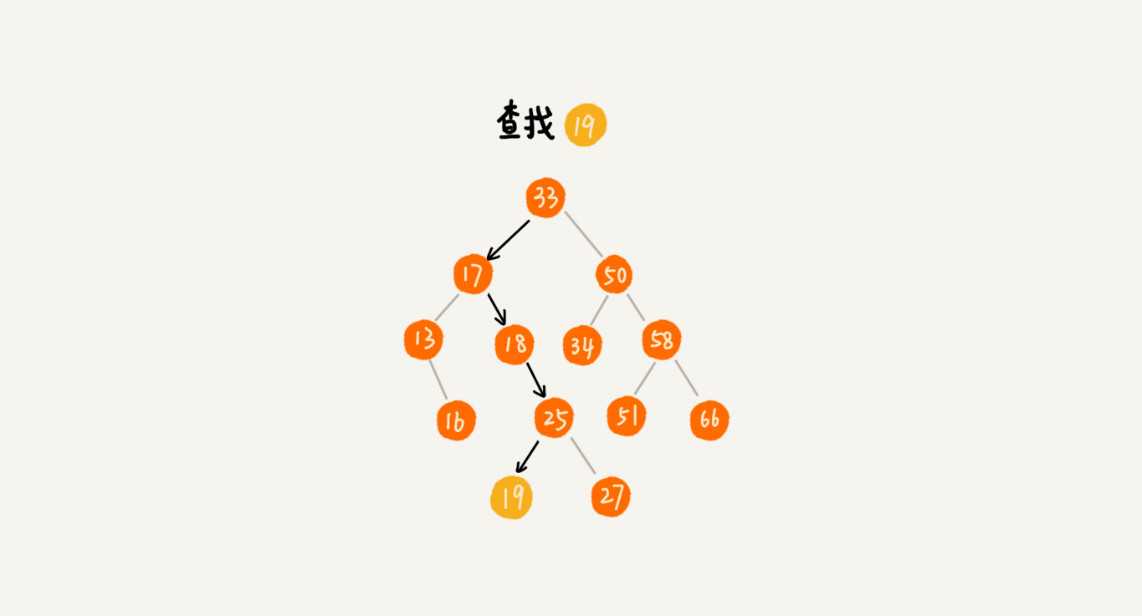
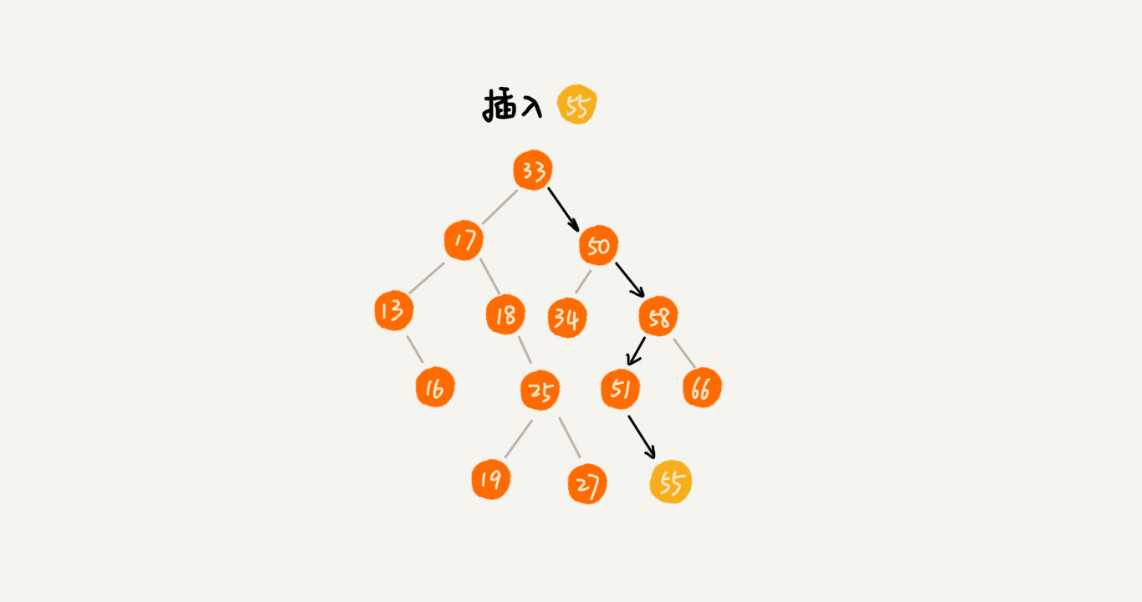
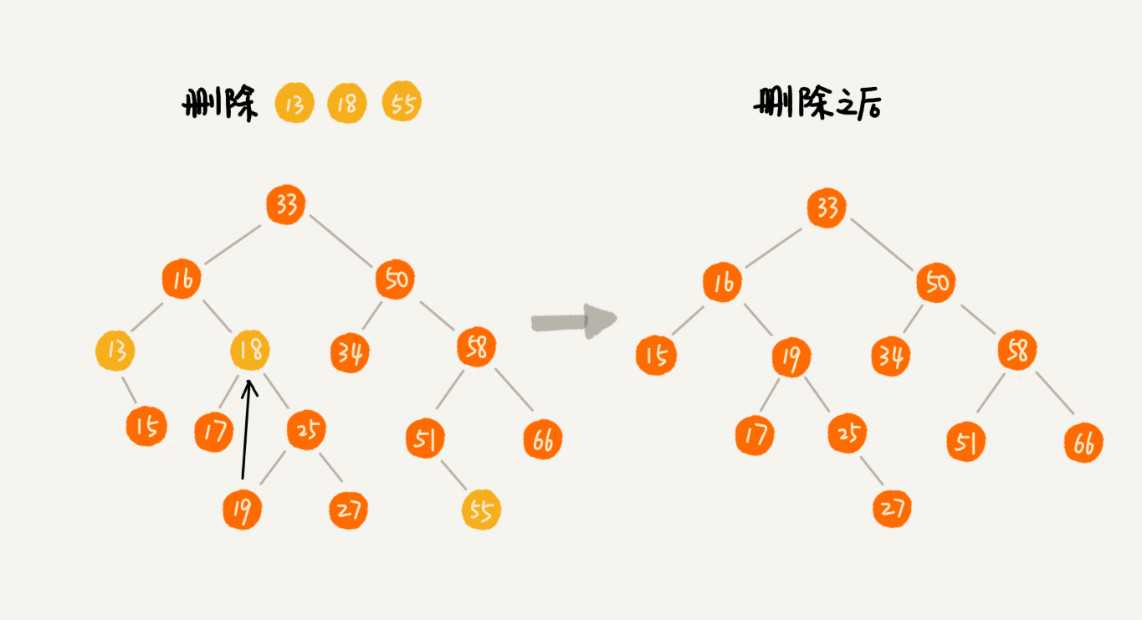
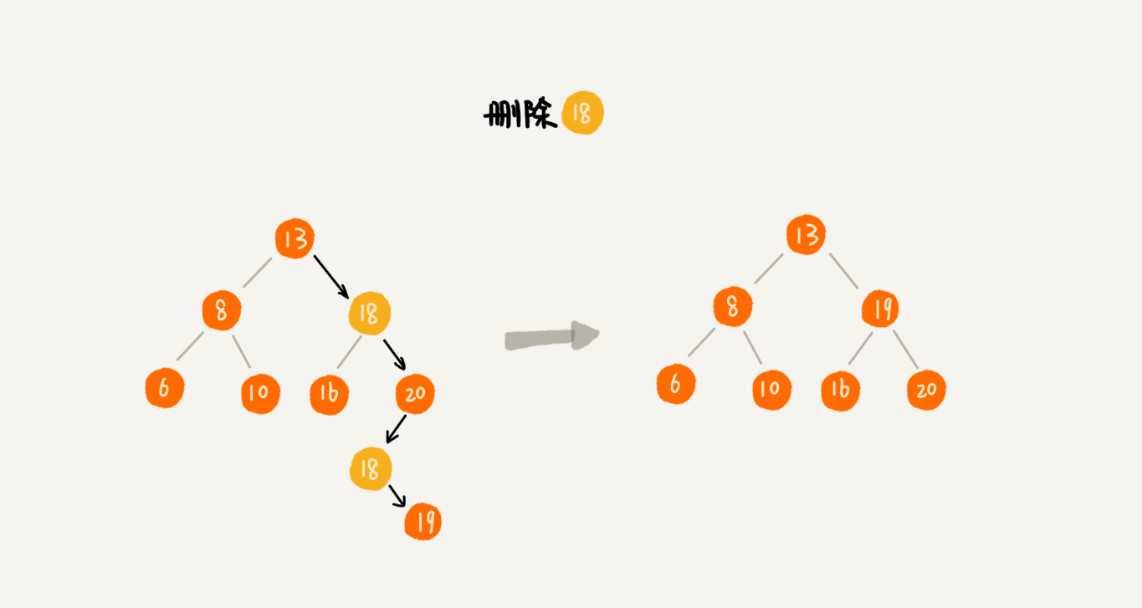
删除是从右子树中找到最小的数，替换被删除的元素。

二叉查找树的其它操作：

可以快速的找到最大节点，最小节点，前驱节点，后继节点。

中序遍历可以输出有序的数据序列，时间复杂度是O（N）

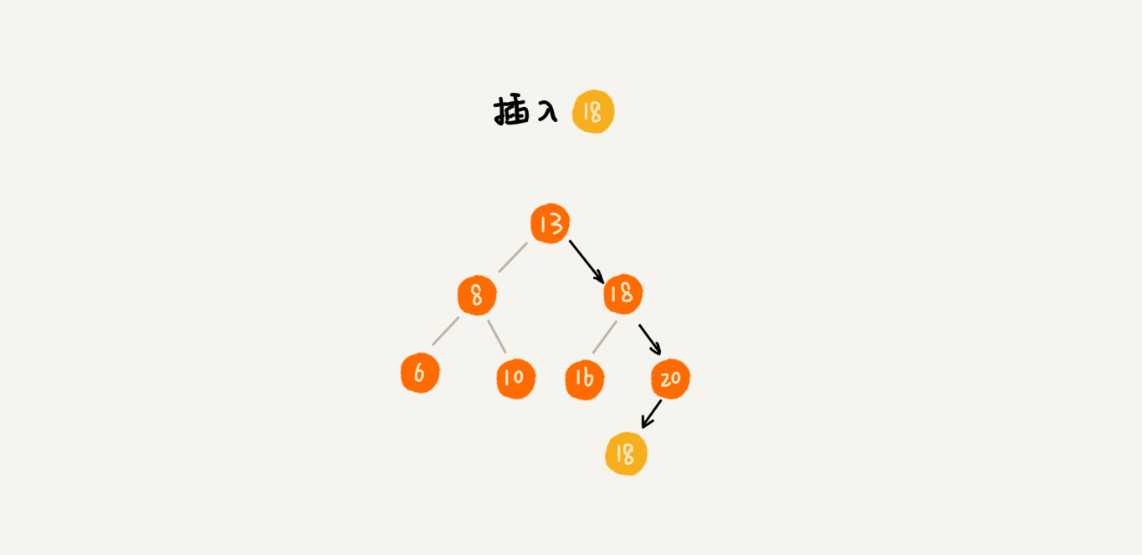
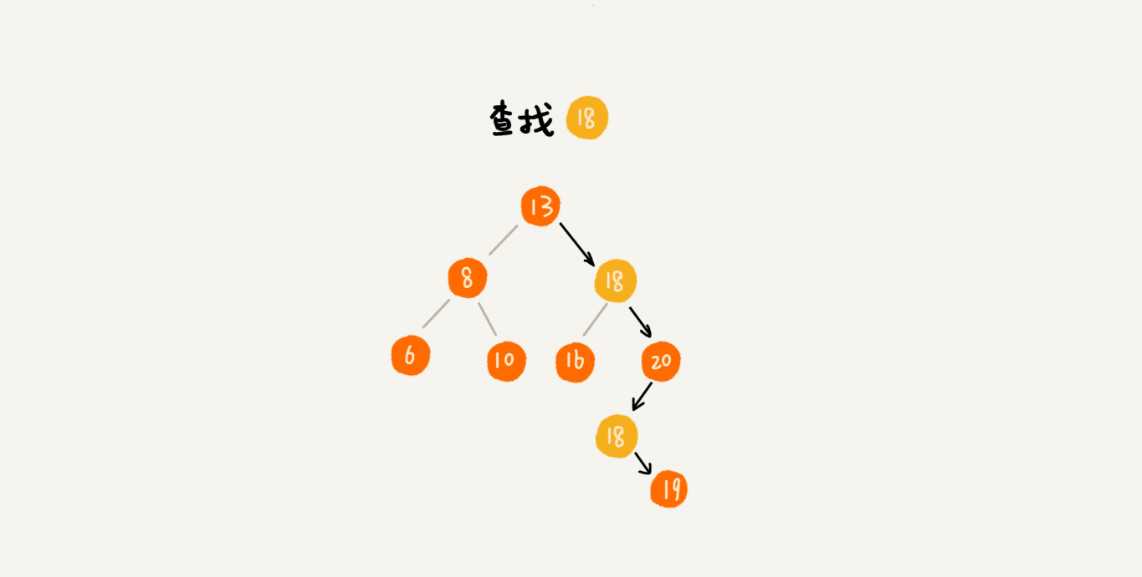
支持重复数据的二叉树

第一：把值相同的数据存储在同一个节点上。

第二：放到这个节点的右子树。那么查找和删除的时候就要都去考虑。

二叉查找树的时间复杂度，退化成了链表，时间复杂度就是O(N)

满二叉树，完全二叉树的时间复杂度都是和树的高度相关的。那么怎么求树的高度？

l层范围是【log2(n+1),log2n + 1】

完全二叉树的高度小于等于logn.

第k层的节点个数就是2^（k-1）

平衡二叉树的高度接近logn ,时间复杂度是O（logn）

总结：散列表是无序存储，

散列表扩容耗时，遇到冲突，性能不稳定。

设计复杂。