信息论-熵

Posted 2021-01-26 shensobaolibin

定义

　　熵是从整个集合的统计特性所考虑的

　　表示信源输出前信源的平均不确定性

　　表示信源输出后每个符号携带的平均信息

 

　　I(p)只能表示信源中每个符号的信息量，不能作为信源总体的信息量

公式:

　　H(x) = E(log 1/p(a_i))

   　　　 = -∑p(a_i) log p(a_i)

 

自信息

　　发出的消息所携带的信息量， 用I(x)计算

　　在消息a中每个符号携带的平均信息量 自信息/符号个数

　　自信息不是熵　　

 

联合熵与条件熵

　　对于信源来说∑p(a_i) = 1

　　对于联合熵来说∑∑p(a_ia_j) = 1

　　p(a_ia_j) = p(a_i|a_j) * p(a_j)

　　 若信源的输出与上一个输出的字符有关系 上一个字符为a_j的话，这一个为a_i个概率为 p(a_i|a_j)

　　联合熵为H(x_ix_j)  = -∑∑p(a_ia_j) log p(a_ia_j) 用于表示信源输出长度为2的平均不确定性

　　条件熵为H(x_i|x_j)  = -∑∑p(a_i|a_j) p(a_j)log p(a_i|a_j)=-∑∑p(a_ia_j) log p(a_i|a_j) 随机序列x_ix_j的联合符号集上的条件自信息量的数学期望

 

　　用公式可以推出

       

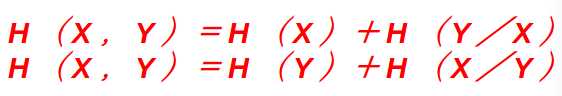
熵的意义

　　H(X)：表示信源中每个符号的平均信息量（信源熵）

　　H(Y)：表示信宿中每个符号的平均信息量（信宿熵）

　　H(X|Y)：表示在输出端接收到Y的全部符号后，发送端X尚存的平均不确定性。这个对X尚存的不确定性是由于干扰引起的。信道疑义度(损失熵，含糊度)

　　H(Y|X)：表示在已知X的全部符号后，对于输出Y尚存的平均不确定性。信道散布度(噪声熵)

　　H(XY)：表示整个信息传输系统的平均不确定性（联合熵）

 

 一些性质

　　若原信源 X 中有一个符号分割成了m个元素(符号)，这m个元素的概率之和等于原元素的概率，而其他符号的概率不变，则新信源的熵增加

　　熵的增加量等于由分割而产生的不确定性量