内螺旋方阵 spiral

Posted 2021-01-26 zhangshuojuruo

【题目描述】：

下面是一个5×5阶的螺旋方阵,编程打印出此形式的n×n阶方阵(顺时针旋进)。

   1  2  3  4  5

   16 17 18 19  6

   15 24 25 20  7

   14 23 22 21  8

   13 12 11 10  9

##【输入描述】：

一个数N

##【输出描述】：

输出N×N阶方阵，每个数间用一个空格隔开。

##【样例输入】：

   5

##【样例输出】：

   1 2 3 4 5

  16 17 18 19 6

  15 24 25 20 7

  14 23 22 21 8

  13 12 11 10 9

##【样例说明】：

##【时间限制、数据范围及描述】：

时间：1s 空间：64M

N <= 1000

5*5例图：

 

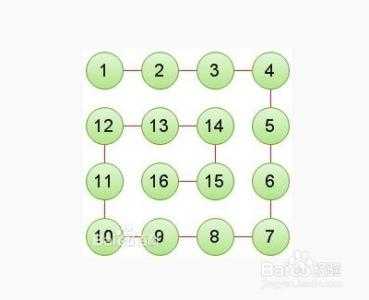
通俗写法（根据方向）：

#include <cstdio>
#include <iostream>
using namespace std;
int a[5000][5000];
int main()
{
    int m=1,N;
    scanf("%d",&N);
    for(int kid=0;kid<=N/2;kid++)
    {
          for(int j=kid;j<N-kid;j++) a[kid][j]=m++;
          for(int i=kid+1;i<N-kid;i++) a[i][N-kid-1]=m++;
          for(int j=N-kid-2;j>=kid;j--) a[N-kid-1][j]=m++;
          for(int i=N-kid-2;i>kid;i--) a[i][kid]=m++;
    }
    for(int i=0;i<N;i++)
    {
        for(int j=0;j<N;j++)
            printf("%d ",a[i][j]);
            cout<<endl;
    }
    return 0;
}

另一种是探究规律：

先从表面看：

通过观察上图，可知：

（1）以顺时针呈方形旋转；

（2）每一层边长为n，第二层数字个数为n-2，...，第k层边长为n-2k；

（3）第一层数字个数为4(n-1)，第二层数字个数为4(n-3)，...，第k层数字个数为4(n-2k+1)；

 其余求和不提。

继续观察，第(i，j)位对应何数字？

观察发现：（第几层按k算）(i，j)位于最靠外围的那一层上，即k=min(i，j，n+1-i，n+1-i)。

其次发现：若将方阵剖分为4个相等对角线三角，

       则数字分为四种情况讨论：

                          （1）第j-k+1个数字；

                          （2）第n-2k+i-k+2个数字；

                          （3）第2(n-2k+1)+n-i-k+2个数字；

                          （4）第3(n-2k+1)+n-i-k+2个数字；

至于图片，哪日我做好后发给大家，望大家多多包涵，请自行理解：

上代码：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
int duck,LUOXUAN[5000][5000],dog;
int main(){
    cin>>duck;
    for(int i=1;i<=duck;i++){
        for(int j=1;j<=duck;j++){
            dog=min(min(i,j),min(1+duck-j,1+duck-i));
            LUOXUAN[i][j]=((duck+1-dog)*(dog-1))*4;
            if(j>=i)
              if(i+j<=duck+1)
                  LUOXUAN[i][j]+=j+1-dog;
                else
                      LUOXUAN[i][j]+=duck+i+2-dog*3;
                      else
                        if(i+j<=duck+1)
                          LUOXUAN[i][j]+=duck*4+5-i-dog*7;
                          else
                                LUOXUAN[i][j]+=duck*3+4-j-dog*5;
                }
    } 
    for(int i=1;i<=duck;i++){
        for(int j=1;j<=duck;j++){
            printf("%d ",LUOXUAN[i][j]);
        }
        cout<<endl;
    } 
    return 0;
} 

Thank you very much!

经验不足，还望多多海涵！

才学会，顺便跟大家分享分享，这也是一只菜鸟的日志啦！！！