朴素贝叶斯

Posted 2021-01-25 yongfuxue

常用tricks

1）平滑技术：拉普拉斯平滑

 

 

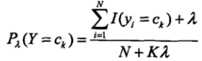
2）对极大似然式子取对数

算法理论

判断一个样本x属于哪个类别y1, y2, y3……, 即是判断max( P(y1|x), P(y2|x), P(y3|x)….)，若最大值是P(yi|x), 那么样本x就属于i类别。

那么该如何求解P(yk|x)？

 

 

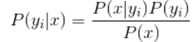
这里c = yk,

因为分母对于所有类别为常数，因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的，所以有：

 

 

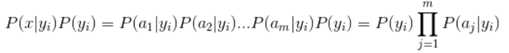
根据我们的样本，很容易计算出P(a1|yi), P(a2|yi)…….,得到一系列P(x|yi)P(yi)的值后，最大值所对应的i值就是样本x的类别。

 

Tip：

1）实际应用中如果P(ak|yi)为0，那么P(x|yi)P(yi)就为0，我们可以将ak初始化为1，分母初始化为2

2）下溢问题，如果P(ak|yi)值很小，那么他们的乘积便会非常小，一种办法就是对乘积去对数。

使用

1）多项分布朴素贝叶斯

我们假设各特征属性条件独立，这里假设特征属性服从多项式分布，P(ak|yi)与下式相等

 

式中 N_yi是训练集T中特征i在类y中出现的次数，N_y是类y中出现所有特征的计数总和。

 

先验平滑因子α>=0 应用于在学习样本中没有出现的特征，以防在将来的计算中出现0概率输出。把α = 1 被称为拉普拉斯平滑(Lapalce smoothing)，而α < 1 被称为利德斯通(Lidstone smoothing)

 

from sklearn.naive_bayes import MultinomialNB

 

2）高斯朴素贝叶斯

我们假设各特征属性条件独立，这里假设特征属性服从多项式分布，P(ak|yi)与下式相等

 

 

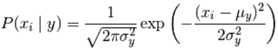
from sklearn.naive_bayes import GaussianNB