严格次小生成树

Posted 2021-01-25 chiyo

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了严格次小生成树相关的知识，希望对你有一定的参考价值。

链接

一道图论题

我觉得如果不是老师讲的话很难想到

（感谢老师.jpg）

首先从相似问题出发，想到了最小生成树。

可以证明次小生成树和最小生成树只有一条边不同。

//此下为不严谨的证明

如果有两条边不同，有两种情况:

（设a替换了u，b替换了v）

1.a>u&&b>v，那么与最小生成树的差距就是 (a-u+b-v) , 如果b不变，差距就是 (a-u)<(a-u+b-v)，所以这不是次小生成树。

2.a<u&&b>v，那么用a替换u以后得到的生成树更小，与条件矛盾。

所以问题转化成了选一条非树边去替换树上的边

为了保证树依然是连通的，非树边只能替换它所在环上的树边

如图（紫色的边只能代替蓝色的边）：

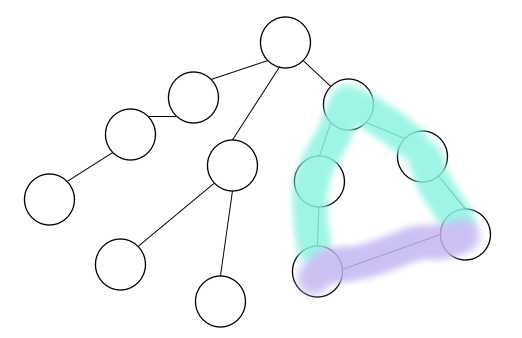
技术分享图片

因为是最小生成树，所以这条非树边肯定大于等于所在环上最长的边

如果大于的话，用它去替换最长的边，否则去替换次长的边，这就需要我们记录环上的最长边和次长边

而环的答案可以转化成这样（由lca分成两条向上的路径）：

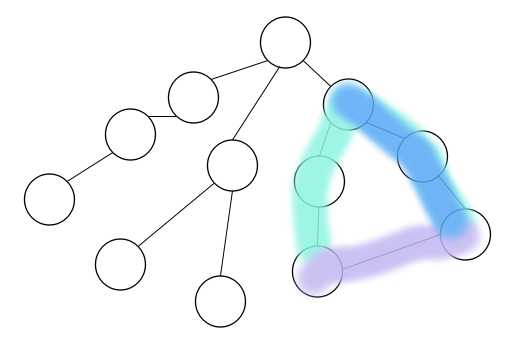
技术分享图片

所以可以考虑倍增求最长边次长边。

big[i][j]=max(big[i][j-1],big[fa[i][j-1]][j-1]);//两个最大值
sma[i][j]=max(sma[i][j-1],sma[fa[i][j-1]][j-1]);//两个次大值
if(big[i][j-1]!=big[fa[i][j-1]][j-1])
      sma[i][j]=max(sma[i][j],min(big[i][j-1],big[fa[i][j-1]][j-1]));//剩下的较小的最大值

然后用类似于lca的跳法，求出每条非树边答案，记录最小差值，最后输出最小生成树+最小差值即可。

复杂度为 mlog(n)

注释都在代码里了，为了清晰一些，把大部分代码放到了函数里，其实拿出来会快很多。

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<algorithm>
  4 #include<string>
  5 #include<cstring>
  6 #define N 500005
  7 using namespace std;
  8 int n,m;
  9 
 10 int h[N],tot=0;
 11 struct yyy{
 12     int y,nxt,z;
 13 }e[N<<1];
 14 inline void ad(int x,int y,int z){
 15     ++tot;
 16     e[tot].y=y;e[tot].z=z;e[tot].nxt=h[x];
 17     h[x]=tot;
 18 }
 19 //建树相关 
 20 int f[N];
 21 struct node{
 22     int x,y,z;
 23     int tag;
 24 }t[N<<1];
 25 long long sumtr=0;
 26 inline bool cmp(node a,node b){
 27     return a.z<b.z;
 28 }
 29 inline int find(int x){
 30     return f[x]==x?f[x]:f[x]=find(f[x]);
 31 }
 32 inline void kru(){
 33     sort(t+1,t+m+1,cmp);
 34     for(int i=1;i<=m;i++){
 35         int fx=find(t[i].x);
 36         int fy=find(t[i].y);
 37         if(fx!=fy){
 38             f[fx]=fy;
 39             t[i].tag=1;//标记树边 
 40             sumtr+=t[i].z;//记录大小 
 41             ad(t[i].x,t[i].y,t[i].z);
 42             ad(t[i].y,t[i].x,t[i].z);
 43         }
 44     }
 45 }
 46 //最小生成树 
 47 int fa[N][25],dep[N];
 48 int big[N][25],sma[N][25];//big/sma[i][j]表示以i为起点向上2^j长度的路径的最大/次大值 
 49 inline void dfs(int u,int pa){
 50     for(int i=h[u];i;i=e[i].nxt){
 51         int y=e[i].y;
 52         if(y!=pa){
 53             dep[y]=dep[u]+1;
 54             fa[y][0]=u;
 55             big[y][0]=e[i].z;
 56             sma[y][0]=-1;
 57             dfs(y,u);
 58         }
 59     }
 60 }
 61 inline void pre(){
 62     for(int j=1;j<=20;j++)
 63         for(int i=1;i<=n;i++){
 64             fa[i][j]=fa[fa[i][j-1]][j-1];
 65             big[i][j]=max(big[i][j-1],big[fa[i][j-1]][j-1]);
 66             sma[i][j]=max(sma[i][j-1],sma[fa[i][j-1]][j-1]);
 67             if(big[i][j-1]!=big[fa[i][j-1]][j-1])
 68                 sma[i][j]=max(sma[i][j],min(big[i][j-1],big[fa[i][j-1]][j-1]));
 69         }
 70 }
 71 //预处理 （prepare) 
 72 inline int lca(int x,int y){
 73     if(dep[x]<dep[y])swap(x,y);
 74     for(int j=20;j>=0;j--)
 75         if(dep[fa[x][j]]>=dep[y])
 76             x=fa[x][j];
 77     if(x==y)return x;
 78     for(int j=20;j>=0;j--)
 79         if(fa[x][j]!=fa[y][j]){
 80             x=fa[x][j];y=fa[y][j];
 81         }
 82     return fa[x][0];
 83 }
 84 inline int get(int x,int y,int z){
 85     int resin=-1;
 86     for(int j=20;j>=0;j--)
 87         if(dep[fa[x][j]]>=dep[y]){
 88             if(z!=big[x][j])resin=max(resin,big[x][j]);//为了保证严格次大 
 89             else resin=max(resin,sma[x][j]);
 90             x=fa[x][j];
 91         }
 92     return resin;
 93 }
 94 //查询相关 
 95 int main()
 96 {
 97     scanf("%d%d",&n,&m);
 98     for(int i=1;i<=n;i++)f[i]=i;
 99     for(int i=1;i<=m;i++)
100         scanf("%d%d%d",&t[i].x,&t[i].y,&t[i].z);
101     kru();
102     dep[1]=1;
103     dfs(1,0);
104     pre();
105     int ans=1000000000;
106     for(int i=1;i<=m;i++)
107         if(!t[i].tag){
108             int lc=lca(t[i].x,t[i].y);
109             int res=max(get(t[i].x,lc,t[i].z),get(t[i].y,lc,t[i].z));
110             ans=min(ans,t[i].z-res);
111         }
112     printf("%lld",sumtr+ans);
113 }