不光是查找值! "二分搜索"
Posted timhy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了不光是查找值! "二分搜索"相关的知识,希望对你有一定的参考价值。
2018-11-14 18:14:15
二分搜索法,是通过不断缩小解的可能存在范围,从而求得问题最优解的方法。在程序设计竞赛中,经常会看到二分搜索法和其他算法相结合的题目。接下来,给大家介绍几种经典的二分搜索法的问题。
一、从有序数组中查找某个值
1、lowerBound
问题描述:
给定长度为n的单调不下降数列a和一个数k,求满足ai >= k条件的最小的i。不存在的情况下输出n。
限制条件:
1 <= n <= 10 ^ 6
0 <= ai < 10 ^ 9
0 <= k <= 10 ^ 9
问题求解:
如果使用朴素的解法按照顺序依次查找的话,也可以求得答案。但是如果利用数列的有序性这一条件,则可以得到更高效的算法,也就是采用二分搜索的方法来进行求解。
这个算法除了在有序数列查找值的问题上很有用处外,在求最优解的问题上也非常有用。
让我们考虑一下“求满足某个条件C(x)的最小的x”这一问题。对于任意满足C(x)的x,如果所有的x‘ >= x也满足C(x‘)的话,那么我们就可以使用二分法来求得最小的x。首先我们将左端点设置为不满足C(x)的值,右端点设置为满足C(x)的值。然后每次取中点,判断中点是否满足并缩小范围,直到范围足够小为止。最后ub就是要求的那个最小值。
最大化的问题也可以使用同样的方法进行求解。
// (lb, ub]
private int lowerBound(int[] nums, int target) {
int lb = -1;
int ub = nums.length;
while (ub - lb > 1) {
int mid = lb + (ub - lb) / 2;
if (nums[mid] >= target) ub = mid;
else lb = mid;
}
return ub;
}
2、upperBound
问题描述:
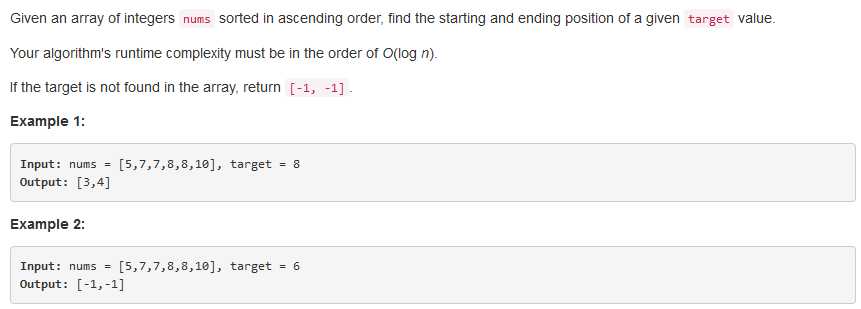
问题求解:
public int[] searchRange(int[] nums, int target) {
if (nums == null || nums.length == 0) return new int[]{-1, -1};
int lb = lowerBound(nums, target);
int ub = upperBound(nums, target);
if (lb == nums.length || nums[lb] != target) lb = -1;
if (ub == 0 || nums[ub - 1] != target) ub = 0;
return new int[]{lb, ub - 1};
}
// (lb, ub]
private int lowerBound(int[] nums, int target) {
int lb = -1;
int ub = nums.length;
while (ub - lb > 1) {
int mid = lb + (ub - lb) / 2;
if (nums[mid] >= target) ub = mid;
else lb = mid;
}
return ub;
}
// (lb, ub]
private int upperBound(int[] nums, int target) {
int lb = -1;
int ub = nums.length;
while (ub - lb > 1) {
int mid = lb + (ub - lb) / 2;
if (nums[mid] > target) ub = mid;
else lb = mid;
}
return ub;
}
二、假定一个解并判断是否可行
Cable master POJ 1064
问题描述:
有N条绳子,它们的长度分别为Li。如果从它们中切割出K条长度相同的绳子的话,这K条绳子每条最长能有多长?答案保留到小数点后2位。
限制条件:
1 <= N <= 10000
1 <= K <= 10000
1 <= Li <= 100000
问题求解:
这个问题可以使用二分搜索非常容易的解决。让我们套用二分搜索的模型试着解决一下这个问题。令:
条件C(x) := 可以得到K条长度为x的绳子
则问题变成了求满足C(x)条件的最大x。在区间初始话的时候,只需要使用充分大的数INF(> MaxL)作为上界即可:
lb = 0
ub = INF
现在问题变成了如何高效的判定C(x)。由于长度为Li的绳子最多可以切出floor(Li / x)段长度为x的绳子,因此
C(x) = (floor(Li / x)的总和是否大于等于K)
它可以在O(n)的时间内判断出来。
本题POJ对精度要求很高,因此有两点需要注意:
1、是需要进行Math.floor(x * 100) / 100,避免四舍五入的问题
2、使用DecimalFormat对输出的精度进行控制
import java.text.DecimalFormat;
import java.util.Scanner;
public class CableMaster {
int n;
int k;
double[] l;
private boolean C(double x) {
long res = 0;
for (double i : l) res += (int) (i / x);
return res >= k;
}
public void cableMaster() {
// 求最大值[lb, ub)
double lb = 0;
double ub = 100001;
// 重复循环直到解的范围足够小
for (int i = 0; i < 100; i++) {
double mid = lb + (ub - lb) / 2;
if (C(mid)) lb = mid;
else ub = mid;
}
DecimalFormat df = new DecimalFormat("0.00");
lb = Math.floor(lb * 100) / 100;
System.out.println(df.format(lb));
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
CableMaster cm = new CableMaster();
while (sc.hasNext()) {
cm.n = sc.nextInt();
cm.k = sc.nextInt();
cm.l = new double[cm.n];
for (int i = 0; i < cm.n; i++) {
cm.l[i] = sc.nextDouble();
}
cm.cableMaster();
}
}
}
三、最大化最小值
Aggressive Cows POJ 2456
问题描述:
农夫约翰搭建了一间有N间牛舍的小屋。牛舍排在一条直线上,第i号牛舍在xi的位置。但是他的M头牛对小屋很不满意,因此经常互相攻击。约翰为了防止牛之间互相伤害,因此决定把每头牛都放在离其他牛尽可能远的位置。也就是要最大化最近两头牛之间的距离。
限制条件:
2 <= N <= 100000
2 <= M <= N
0 <= xi <= 10 ^ 9
问题求解:
类似的最大化最小值或者最小化最大值的问题,通常用二分搜索法就可以很好的解决。我们定义:
C(d) := 可以安排牛的位置使得最近的两头牛的距离不小于d
那么问题就变成了求满足C(d)的最大的d。另外最近两头距离不小于d也就是所有的牛的间距都大于等于d。
判定C(d)可以使用贪心法进行判断:
对牛舍位置进行排序;
第一头牛放在x0牛舍;
如果第i头牛放到了第xj,那么第i + 1头牛就要放入最近的满足xk - xj >= d的牛舍。
import java.util.Arrays;
import java.util.Scanner;
public class AggressiveCows {
int n;
int m;
int[] x;
private boolean C(int d) {
int prevIdx = 0;
for (int i = 1; i < m; i++) {
int curIdx = prevIdx + 1;
while (curIdx < n && x[curIdx] - x[prevIdx] < d) curIdx++;
if (curIdx == n) return false;
prevIdx = curIdx;
}
return true;
}
public int aggressiveCows() {
Arrays.sort(x);
int lb = 0;
int ub = x[n - 1];
while (ub - lb > 1) {
int mid = lb + (ub - lb) / 2;
if (C(mid)) lb = mid;
else ub = mid;
}
return lb;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
AggressiveCows ac = new AggressiveCows();
while (sc.hasNext()) {
ac.n = sc.nextInt();
ac.m = sc.nextInt();
ac.x = new int[ac.n];
for (int i = 0; i < ac.n; i++) {
ac.x[i] = sc.nextInt();
}
System.out.println(ac.aggressiveCows());
}
}
}
四、最大化平均值
问题描述:
有n个物品的重量和价值分别是wi和vi。从中选出k个物品使得单位重量的价值最大。
限制条件:
1 <= k <= n <= 10 ^ 4
1 <= wi, vi <= 10 ^ 6
问题求解:
一般最先想到的方法可能是把物品按照单位重量进行排序,从大到小进行选取。但是这个方法在本题中是不可行的。那么应该如何求解呢?
实际上,对于本题,使用二分搜索法可以很好的解决。我们定义
条件C(x) : 可以选择使得单位重量的价值不小于x
因此原问题就变成了求满足C(x)的最大的x。那么应该怎么判断C(x)是否可行呢?假设我们选择了某个物品的集合S,那么他们的单位重量价值为:
sum(vi) / sum(wi)
因此就变成了判断是否存在S满足以下的条件
sum(vi) / sum(wi) >= x
把这个不等式进行变形就可以得到
sum(vi - wi * x) >= 0
因此,就可以进行贪心的选取,对vi - wi * x的值进行排序,贪心的从中选择k个,看其和是否大于0。由于每次都需要排序,所以判断的时间复杂度为O(nlogn)。
五、Follow Up
-
Search in Rotated Sorted Array
问题描述:
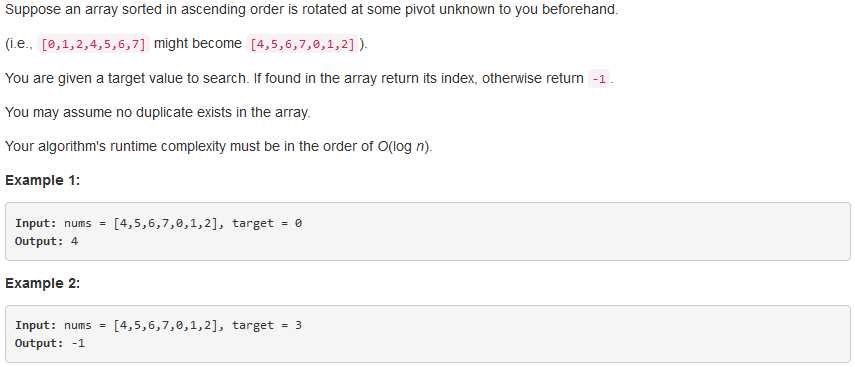
问题求解:
因为没有重复,所以可以直观的通过mid和r比较来判断当前的mid是在前半段还是后半段。
public int search(int[] nums, int target) {
if (nums == null || nums.length == 0) return -1;
int l = 0;
int r = nums.length - 1;
// [l, r]
while (r - l + 1 > 0) {
int mid = l + (r - l) / 2;
if (nums[mid] == target) return mid;
if (nums[mid] > nums[r]) {
// 这里的判断条件是关键
if (nums[mid] > target && target >= nums[l]) r = mid - 1;
else l = mid + 1;
}
else {
if (target > nums[mid] && target <= nums[r]) l = mid + 1;
else r = mid - 1;
}
}
return -1;
}
-
Search in Rotated Sorted Array II
问题描述:
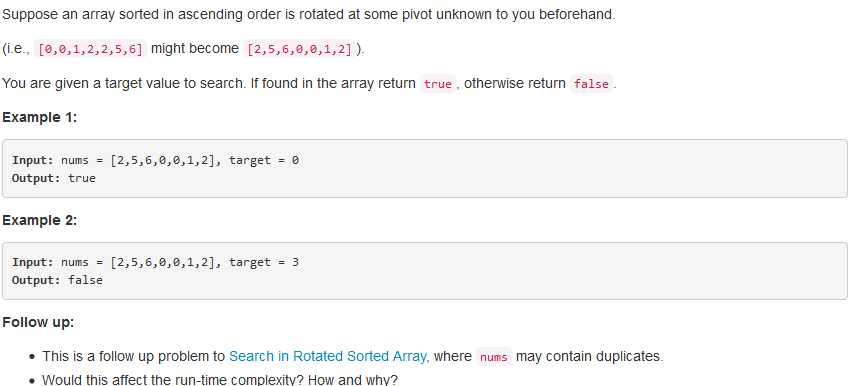
问题求解:
带有重复值的问题就是有可能mid和两端的值是相等的,在这种情况下就没有办法进行有效的判断了,所以需要对两端的值进行一下去重操作,然后再使用上述的算法进行二分查找。
public boolean search(int[] nums, int target) {
if (nums == null || nums.length == 0) return false;
int l = 0;
int r = nums.length - 1;
while (r - l + 1 > 0) {
while (l < r && nums[l] == nums[l + 1]) l++;
while (r > l && nums[r] == nums[r - 1]) r--;
int mid = l + (r - l) / 2;
if (nums[mid] == target) return true;
if (nums[mid] > nums[r]) {
if (target >= nums[l] && target < nums[mid]) r = mid - 1;
else l = mid + 1;
}
else {
if (target > nums[mid] && target <= nums[r]) l = mid + 1;
else r = mid - 1;
}
}
return false;
}
以上是关于不光是查找值! "二分搜索"的主要内容,如果未能解决你的问题,请参考以下文章