最坏情况为线性的选择算法

Posted 2021-01-25 w-j-c

基本思想

主体上是在期望为线性的选择算法上进行改进,将其中的随机的划分元素改为取中位数,使划分更均匀,从而达到最坏时时间复杂度也为线性.需要注意的是实现时里面的索引很晕,别搞混了.我就是先写了个很乱,然后实在改不下去了,就重写了,总共我大概写了5,6个小时吧.(可能我太菜了)

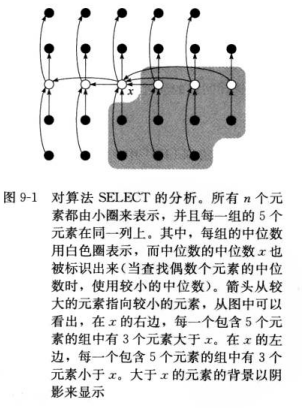
图解

代码

伪代码

这里书中未给伪代码,仅给了整个算法的流程,但并不影响我们的实现

C代码

#include <stdio.h>
#define N 50

void show(int *a, int p, int r);
int Partition(int * a, int p, int r, int x)//以值x来进行分割
{
    int k;
    int pos;
    for(k = p; k <= r; k++)//先把值x与末尾r交换位置,不太好,因为我还遍历了数组来找x的索引值
    {
        if(a[k] == x)
            pos = k;
    }
    int temp;
    int t = a[pos];
    a[pos] = a[r];
    a[r] = t;
    int i, j;
    i = p-1;
    for(j = p; j <= r; j++)
    {
        if(a[j] <= t)
        {
            i+=1;
            temp = a[i];
            a[i] = a[j];
            a[j] = temp;
        }
    }
    return i;//返回划分后的x所对应的索引
}

int Insertion_sort(int * a, int p, int r)//用来对每组元素进行插排
{
    int i, j;
    for(i = p+1; i <= r; i++)
    {
        j = i;
        while(j > p && a[j] < a[j-1])
        {
            int temp = a[j];
            a[j] = a[j-1];
            a[j-1] = temp;
            j--;
        }
    }
}

int Select(int *a, int p, int r, int i, int len)//返回第i个元素的值
{
    if(p==r)//仅一个元素时直接返回
    {
        return a[p];
    }

    int midval[N];
    int group = len%5==0 ? len/5 : len/5+1;
    if(len%5==0)//每组刚好5人
    {
        int i;
        for(i = 0; i < group; i++)
        {
            Insertion_sort(a,p+5*i,p+5*i+4);    
            midval[i] = a[p+i*5+2];
        }   
    }
    else//最后一组不满5人
    {
        int i;
        for(i = 0; i < group-1; i++)
        {
            Insertion_sort(a,p+5*i,p+5*i+4);
            midval[i] = a[p+i*5+2];
        }
        //单独处理最后一组
        int lastgroupsize = len%5;
        Insertion_sort(a,p+5*i,r);
        midval[i] = a[p+i*5+lastgroupsize/2];
    }
    
    int pos2 = Select(midval,0,group-1,group/2,group);//对midval[]递归查找其中位数
    int q = Partition(a,p,r,pos2);//以中位数pos2来划分元素

    int k = q-p;//划分元素的相对位置
    if(i == k)
        return a[q];//划分元素刚好为所查元素,返回 
    else if(i < k)
        return Select(a,p,p+k-1,i,k);//继续处理左半边
    else 
        return Select(a,p+k+1,r,i-k-1,r-p-k);//继续处理右半边
}

int main()
{
    int a[]  = {34,65,21,32,555,11,4,78,64,99,25,100,24};
    int len = sizeof(a)/sizeof(int);
    int k;
    int i;
    for(i = 0; i < len; i++)
    {
        printf("%d ", a[i]);
    }
    printf("
input nth to search
");
    scanf("%d",&k);
    int ans = Select(a,0,12,k,13);
    printf("ans %d
", ans);
    return 0;
}
//算法流程不难,但实现起来其中的细节很多,尤其这里面的下标很绕人

时间复杂度

O(n)