原文链接http://www.cnblogs.com/zhouzhendong/p/8424570.html
对于动态树 $(Link-Cut-Tree, LCT)$ 的理解与总结
问题模型
有$n$个节点,每个节点有权值$v_i$,现在有$m$个操作,操作有可能是以下$4$种类型:
$1$ - 连接两个节点
$2$ - 断开两个节点之间的边
$3$ - 修改某一个节点的权值
$4$ - 询问两点之间的节点权值和
保证操作和询问合法,并且输入数据保证任何时刻图中不出现环。
$1\\leq n,m\\leq100000$
做法
$\\circ$ 树链剖分?时间复杂度$O(n+m\\ log^2\\ m)$,但是显然不行!!。
于是$LCT$来了。
$LCT,Link-Cut-Tree$即动态树。(又是$Tarjan$提出来的……$Tarjan$大神太强了!)
时间复杂度$O(m\\ log\\ n)$
$LCT$
$LCT$是一种用在树上几乎无敌的算法,但是他也有致命弱点——大常数,可能会抵一个$log$……
在学$LCT$之前,我们要先会$Splay$,如果您不会,请先学习$Splay$。
$LCT$里面可能存在着多个$Splay$,这个神奇的东西!
以下图所表示的树为例。
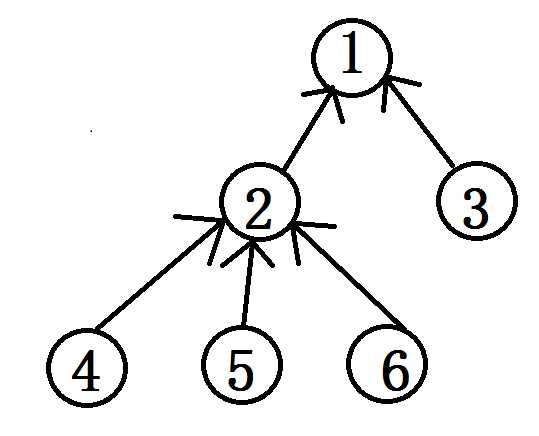
无根树的边是无向的,但是我这里为什么画成有向呢,待会儿就知道了。
$Task\\ 1:\\ \\ \\ \\ \\ Access$
$Access$操作是一切的基础!
$Access(x)$的作用是从$x$到他的祖先打通一条路径,使他们在$Splay$结构中成为一段连续的节点。
比如$Access(4)$的效果如下:
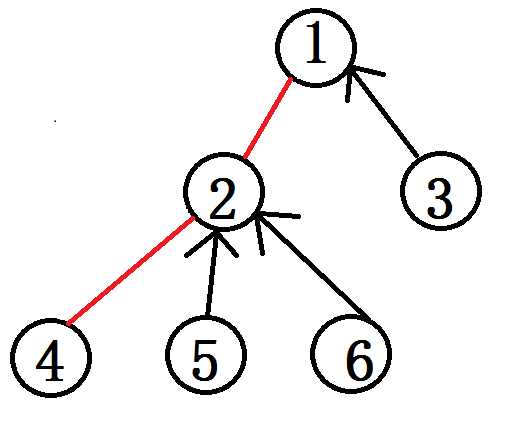
于是$4\\rightarrow2\\rightarrow1$就成为了一条链,并且在Splay中是连续的一段位置。
注意,我们这里默认在$splay$中儿子是父亲的右儿子。比如(在$splay$中)4是2的右儿子。
$Task\\ 2:\\ \\ \\ \\ \\ Splay$
$Splay=$神奇的相对位置!
$Splay$的作用就是对于一个连通块,在不改变树的形态的原则下,通过$Splay$的操作来调整一个节点的位置。
比如,在上图,$Splay(2)$的效果如下:
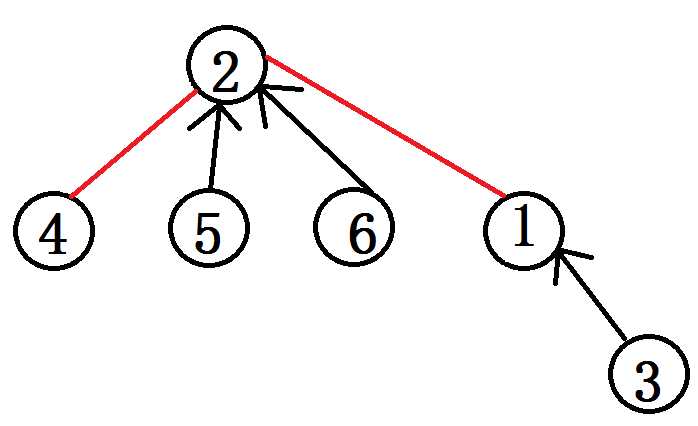
$Task\\ 3:\\ \\ \\ \\ \\ Rever$
$Rever$ - 连通块换根!
开始脑补!
$ Rever(x) ing$
考虑我们需要把一个点提到根的位置,办法是通过$splay$。
而$splay$之前,我们必然要使得$x$到根的路径被打通。
所以先$Access(x)$,然后$Splay(x)$。
考虑到我们之前的$Splay$中都是只有右儿子的,但是现在$Splay$之后,当前链上的节点都是只有左儿子的啦!于是我们淡定的打上翻转标记,万事大吉。
$Task\\ 4:\\ \\ \\ \\ \\ Link$
关键部分开始了!
考虑连接两个节点$x,y$。
这不是很简单吗!
先让$x$做$x$所在连通块的根(为了让他的father指针空出来连y)
然后让$father_x=y$,搞定!
$Task\\ 5:\\ \\ \\ \\ \\ Cut$
关键部分2.0
考虑分离两个点。
首先,开始套路:
$Rever(x)$
然后我们要让$x$变成$y$的直接儿子。
于是我们$Access(y),\\ Splay(y)$
显然这个时候,$x$一定是$y$的左儿子。
于是$father_x=son_{y,0}=0;$
然后就断开了。$ok$!
那么如果完成上面的问题呢?
只要在$splay$的过程中维护一个$sum$即可。询问的时候也只要$splay$几下,然后通过处理好的$sum$回答问题即可。
如果您想更具体的感受这个操作,请看习题。
贴模板
$LCT$讲完了!
结合模板学习您就可以得到更深的理解!
(该模板如果有错,欢迎留言纠正,谢谢!)
const int N=50005;
int n,m;
int fa[N],son[N][2],rev[N],val[N],sum[N];
bool isroot(int x){
return son[fa[x]][0]!=x&&son[fa[x]][1]!=x;
}
void pushup(int x){
sum[x]=sum[son[x][0]]+sum[son[x][1]]+val[x];
}
void pushdown(int x){
rev[son[x][0]]^=1,rev[son[x][1]]^=1;
swap(son[x][0],son[x][1]);
}
void pushadd(int x){
if (!isroot(x))
pushadd(fa[x]);
pushdown(x);
}
int wson(int x){
return son[fa[x]][1]==x;
}
void rotate(int x){
if (isroot(x))
return;
int y=fa[x],z=fa[y],L=wson(x),R=L^1;
if (!isroot(y))
son[z][wson(y)]=x;
fa[x]=z,fa[y]=x,fa[son[x][R]]=y;
son[y][L]=son[x][R],son[x][R]=y;
pushup(y),pushup(x);
}
void splay(int x){
pushadd(x);
for (int y=fa[x];!isroot(x);rotate(x),y=fa[x])
if (!isroot(y))
rotate(wson(x)==wson(y)?y:x);
}
void access(int x){
int t=0;
while (x){
splay(x);
son[x][1]=t;
pushup(x);
t=x;
x=fa[x];
}
}
void rever(int x){
access(x);
splay(x);
pushrev(x);
}
void link(int x,int y){
rever(x);
fa[x]=y;
}
void cut(int x,int y){
rever(x);
access(y);
splay(y);
fa[x]=son[y][0]=0;
}
习题
BZOJ2002 [Hnoi2010]Bounce 弹飞绵羊 LCT
BZOJ2049 [Sdoi2008]Cave 洞穴勘测 LCT
BZOJ2843 极地旅行社 LCT
BZOJ3091 城市旅行 LCT
BZOJ2631 tree LCT
BZOJ1180 [CROATIAN2009]OTOCI LCT
BZOJ2594 [Wc2006]水管局长数据加强版 LCT kruskal
BZOJ3514 Codechef MARCH14 GERALD07加强版 LCT
BZOJ3669 [Noi2014]魔法森林 LCT
BZOJ2759 一个动态树好题 LCT 逆元