网格简化技术研究报告

Posted 2021-01-24 lvweiwolf

网格简化技术研究报告

吕伟

问题及场景

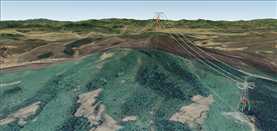
超大场景环境下，为了精细、真实的塔模型，采用分级简化铁塔和绝缘子串模型的方法，利用PageLOD分页细节层次的机制，在不同范围下展现不同精细程度的外观。

简化模型要求速度快、质量高、文件体积小等特点。

网格简化的算法分类

删减法

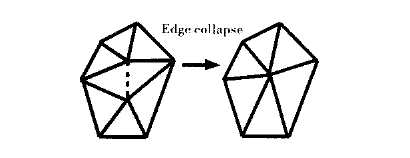
删减法是目前算法中采用最多的一种模型简化操作。该方法通过重复依次删除对模型特征影响较小的几何元素并重新三角化来达到简化模型的目的。根据删除的几何元素的不同，通常又可以分成顶点删除(Vertex removal)法、边折叠(Edge Collapse)法和三角面片折叠(Triangle collapse)法等。

 

采样法

采样法首先将顶点(Vertex)或体素(Voxels)添加到模型表面或模型的三维网格上，然后根据物理或几何误差测度进行顶点或体素的分布调整，最后在一定约束条件下，生成尽可能与这些顶点或体素相匹配的简化模型。采样法适合于无折边、尖角和非连续区域的光滑曲面的简化，对于非光滑表面模型简化效果差。

自适应子分法

自适应子分法通过构造简化程度最高的基网格模型(Base Model)，然后根据一定的规则，反复对基网格模型的三角面片进行子分操作，依次得到细节程度更高的网格模型，直到生成的网格模型与原始模型误差达到给定的阈值。自适应子分算法具备简单、实现方便等特点，但只适用于容易求出基网格模型的一些应用（如地形网格模型简化等），另外简化模型对于具有尖角和折边等特征的保持效果较差。

顶点聚类法

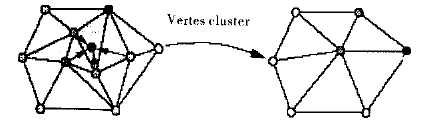
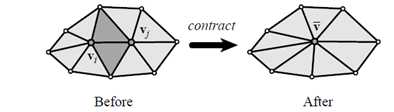
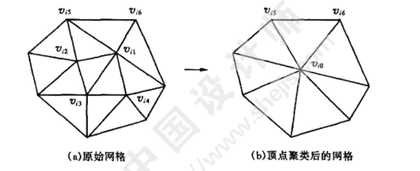
顶点聚类方法根据一定的规则，将原始网格模型中的两个或多个顶点合并成一个顶点，并删除合并顶点后的退化三角形，从而达到简化网格面片数量，实现网格模型简化的目的。下图为顶点聚类法操作示意图，图中将4个顶点聚类合并为一个顶点，并删除相应的退化三角形后，得到简化后的网格模型。边折叠法也可以看成是顶点聚类法中两个顶点合并的情况。顶点聚类法能处理任意拓扑类型的网格模型，算法简单，速度较快。但由于简化误差控制困难，容易丢失较小结构的细节，因此通常简化模型质量不高。

多边形合并(Polygon merging)

多边形合并法通过将近似共面的三角网格面合并成一个平面，然后对形成的平面重新三角化，来实现减少顶点和面片数量的目的。也被称为面片聚类(Face cluster)和超面(Superfaces)法。该方法在合并和三角化过程中可能改变孔洞结构，因此不能保证简化前后模型的拓扑结构。

简化算法的误差测度（度量质量和误差）

误差测度用于度量模型简化的质量和误差，因此它对模型的简化过程和最后的简化结果都具有重要的影响。大多数简化算法采用对象空间(Object-space)的一种或综合几种形式的几何误差(Geometric errors)作为误差测度，一些视点相关算法通常将对象空间的误差转换为屏幕空间(Screen-space)的误差值为误差测度，有些算法也考虑模型的颜色、法向量和纹理坐标等属性误差(Attribute errors)。

几何误差

几何误差测度一般采用欧式空间距离表示。通常有顶点到顶点、顶点到平面和平面到平面的距离等形式。

Hausdorff距离是现有算法中常常用到度量顶点到表面、表面到表面距离的几何误差测度，该距离为两个模型的顶点之间的最小距离中的最大值。

给定欧式空间的两点集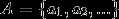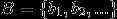，，Haousdorff距离就是用来衡量这两个点集间的距离。

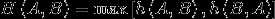
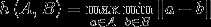
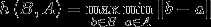
算法过程：

该算法的时间复杂度是O(n，m)，其中n和m分别为集合A和集合B中的点数。

屏幕空间误差计算

视点相关算法常常需要将对象空间误差转换为屏幕空间误差。设对象空间几何误差为e，x为以像素表示的屏幕某方向的分辨率，d是视点到模型对象的距离，θ为视野夹角，则e对应的屏幕空间误差p为：

属性误差（材质、纹理）

网格模型上的三角面片、、法向量、纹理坐标、顶点的颜色是其常见的属性。

网格模型的颜色一般以(r, g, b)三元组形式来表示，各分量分别在[0, 1]中取值。最直接的方法是采用欧式空间距离求解方法来求取颜色的距离。设简化过程的两模型M1、M2的颜色分别表示为(r1, g1, b1)和(r2, g2, b2)，则两模型的颜色距离dc可以表示为：

两个法向量的误差距离dn通常采用角度值进行度量：

多边形表面的纹理坐标用(u, v)坐标对来表示网格模型顶点到二维纹理空间的映射，其中，u，v通常在[0, 1]中取值。一般也是采用欧式空间距离求解方法来计算纹理坐标误差：

 

简化算法的约束条件或运行条件

模型简化过程中或简化算法运行时往往存在一些限制条件，这些条件也决定了算法采用的技术、算法运行效果和模型简化结构等。

细节层次（LOD）

对于各种简化细节层次的LOD模型的管理技术可以分成离散LOD(Discrete LOD)、连续LOD(Continuous LOD)和视点相关LOD技术。

早期简化算法大多采用离散LOD技术。这种技术首先采用离线(offline)方式对原始模型进行预处理，生成一系列不同分辨率的简化模型。在实际运行时，根据需要选择已生成的某个简化模型进行绘制。由于在实时显示绘制时不需要再次进行简化操作，因此该技术具有实时运行速度快、数据存储结构简单等优点。但是因为需要保存多个预处理的中间简化模型，所以占用存储空间大；且在简化预处理时无法考虑视点及实时运行环境因素等要求，只能根据模型本身信息进行简化，因而简化效率不高；同时由于技术限制，预简化生成LOD模型数量不可能过多，粒度不可能太细，因此实时显示绘制时候，在不同简化模型切换过程中会出现画面跳跃、视觉不连续等的效果。离散LOD简化也称为静态简化。

连续LOD技术是对传统的离散LOD技术的改进和发展。与离散LOD技术不同，连续LOD技术的各简化模型不是在预处理中生成，而是通过构造特定的数据结构进行编码存储，在实时显示运行时根据需要生成对应细节层次的简化模型。因此连续LOD技术具有更高的LOD粒度表示，占用空间较小，运行时画面连续性较好等优点；但由于运行时需要进行简化模型的生成处理，因此实时显示速度收到一定影响。连续LOD技术支持多边形网格模型的传输，常被应用于网格模型的各种递进简化算法中。

简化模型的拓扑结构保持

简化过程中是否保持网格模型的拓扑结构不变也是区分不同简化算法的一个重要依据。网格模型的拓扑结构通常指构成网格模型的各三角网格之间的连接关系。衡量模型简化算法是否能保持拓扑结构一般是通过判断网格表面的亏格(Genus)和流型(Manifold)是否在简化过程中保持不变来确定。亏格采用网格表面的孔洞数量来计算。

主要成熟算法

删减算法

最早的删减算法是Schroeder等在1992年提出的顶点删除算法。随后Hoppe提出采用能量法来确定折叠顺序和计算顶点新位置的边折叠简化算法，Schroeder等扩展了边折叠算法，考虑了不相连的顶点对删减问题，提出了顶点对(虚边)折叠算法，Hamann和Gieng等提出的三角形折叠算法相当于两次边折叠的组合，因此效率高，但细化粒度大。边折叠算法后来被广泛应用于基于顶点到平面距离平方和的QEM算法、视点不相关简化算法、视点相关简化算法、递进压缩算法以及递进传输算法。

QEM

QEM(Quadric Error Mactrics，二次误差测度)模型简化算法，具有兼顾执行效率和模型质量的优点。能在考虑颜色，纹理，拓扑等特征的条件下，对三维模型进行任意程度的简化。

其关键思想是将模型中最小Q值的顶点对（Pair Contraction）进行收缩（即：将2个点收缩成1个点），不停地迭代来逐步化简模型。

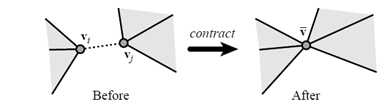
下图为两种类型的顶点对：

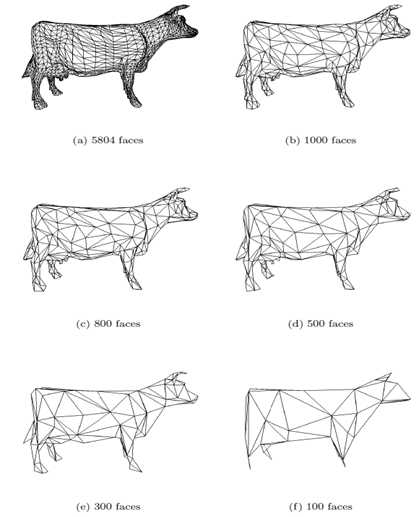
模型试验结果：

二次误差测度

QEM算法的基本操作基于边折叠，误差测度采用的是二次误差测度。二次误差测度最早是由Garland提出，采用点到平面距离的平方作为误差测度。它的优点是具有较高的计算速度，较小的内存消耗，而且得到的简化网格具有较高质量。它是在速度非常快但简化质量很差、速度很慢但简化质量非常好的两类方法之间的一种折中，是一种兼顾了速度和质量的较理想的误差测度。

    在三维欧氏空间中，一个平面可以表示为：，其中时平面的单位法向量，d时常量。点到该平面的距离就可以表示为：

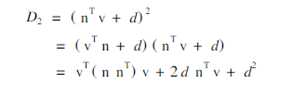
可以定义三元组来表示, ，Q称作二次误差测度或二次矩阵，Q(v)称作二次误差。利用二次误差测度可以方便地实现误差累加，其中。

    二次误差测度在几何上可以解释为：有Q(v) = ε 确定的等值面是椭球面(可能退化)；A是一个对称的半正定矩阵，它的特征值和特征向量决定了椭球面的主轴。

表面属性

    在计算机图形学中， 三角网格模型最常见的表面属性有颜色、纹理和法线。为了使简化模型同初始模型具有良好的相似性， 必须在保持模型几何信息的同时保留这些属性特征。由于点到平面的距离考虑了简化操作对顶点周围区域属性值变化的影响， 可以比较准确地描述局部属性误差， 同时又比点到表面或表面到表面的距离计算简便快捷。因此， 采用点到平面的距离作为属性误差测度， 将二次误差测度应用到属性误差的计算中。

网格模型的每个顶点除了空间坐标外，还具有描述其属性的数值。在网格模型的三角面上， 属性值根据几何位置插值得到。因此， 三角面上的属性值是连续的， 而且两个属性值之间的距离用欧氏距离来度量。

比如对于颜色属性，可以用三维矢量来表示()，所有颜色矢量构成了RGB彩色空间，在RGB彩色空间中点到平面的距离平方同样可以用二次误差Q(v)来计算。边折叠后的新顶点采用子集选择法，不用重新计算顶点的空间位置和属性值，在计算误差的时候不用考虑空间坐标和属性值的相关性，只需分别建立几何二次误差测度和属性二次误差测度，并计算几何和属性误差。

边折叠操作的代价

采用带有颜色属性的模型应用算法，带有其他属性的网格模型可以同理推出。三角网格模型的每个顶点和()来表征几何和颜色信息。为每个三角面建立几何二次误差测度和颜色二次误差测度。各顶点的二次误差测度之和：

当边折叠(, )到顶点v的时候，总的二次误差测度为：

故而边折叠引起的几何误差，颜色属性误差。则总的边折叠代价为：

其中α为颜色属性误差在总代价中的影响系数，可以根据实际情况进行调节。

顶点或面片的合并聚类算法

基于顶点聚类的网格简化算法最早优Rossignac提出， 基本思想是：用一个包围盒把原网格模型包围起来，通过等分包围盒的各棱边将包围盒等分成若干个小的长方体，这样原模型的所有顶点就分别落在这些长方体类；扫描这些长方体，如果某个长方体内有顶点，则把该长方体内的所有顶点删除并生成一个新顶点，这个新顶点是被删除的原顶点的平均加权。这种方法存在着三个局限性：首先，由于原网格模型上的点在空间的分布是未知的，这种方法对包围盒进行等分，可能导致等分后某些区域的长方体内包含很多的顶点，而某些区域的长方体内没有或只有很少的顶点，这一方面造成空间和时间的浪费，另一方面造成模型的某些部分过分简化；其次，生成某个长方体内新顶点时，这种方法只是取简单的加权平均而并没有给出一种较好的误差控制方法；再次，当原网格模型比较特殊时，落在某些长方体内的顶点可能属于原模型差别较大的部分，如果这些顶点聚类成一个顶点就会造成很大的变形。如下图：

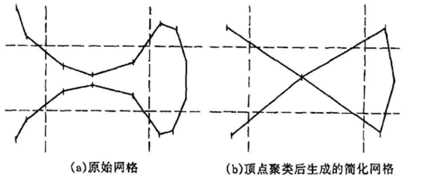
根据以上的算法思路，可以提出一种基于八叉树的顶点聚类网格简化算法，其主要改进的是使用八叉树的方法对原模型包围盒进行自适应划分，同时利用二次误差测度控制简化模型的变形。

算法描述

基本概念

定义1. 空间中一组三角形，沿公共边及在顶点处相邻接，把这样的一组三角形定义为三角网格TM，TM可由顶点集V = (, )和三角形集合 T=(t1, t2, t3 …, tm)所组成的二元组(V, T)来表示。

定义2. 对TM中任一条边，如果该边只为一个三角形所享有，则称该边为边界边，该边的两个顶点被称为边界顶点，该边所在的三角形被称为边界三角形。

定义3. 对TM中任一顶点vi，所有以vi为一个顶点的三角形Tik构成的集合，称为与顶点vi相关的三角形集合Pi

定义4. 对应TM中一个顶点集V = (, )，与V中的每个顶点相关的三角形集合的并集，称为顶点集合V相关的三角形集合T(V)。

顶点聚类的新顶点的生成和误差的度量

首先考虑，如果一些顶点落在一个长方体内时，删除这些顶点后，如何生成一个新顶点以及用该新顶点代替被删除的顶点所产生的误差是多少。这就有一个选择误差标准的问题，这里以点到平面的距离为误差标准。

    假设落在每个长方体顶点和边所构成的图是连通的，考虑一个顶点集合V落在一个长方体内时，如何求新点和简化误差。我们可以先得到与顶点集合V相关的三角形集合T(V)，由前面的假设不难发现，这个三角形集合构成了原网格模型上的一个区域。下图是一个简单的例子，顶点集合为{v1, v2, v3, v4}，聚类为v0。如果顶点集合V聚类为顶点，定义这个聚类带来的误差为到三角形集合T(V)中每个三角形所在平面的距离平方之和加上V中的顶点到每个与相关的三角形所在平面的距离平方之和，即

为了使尽可能的小，可以对上式的x, y, z求偏导，使其等于零，即

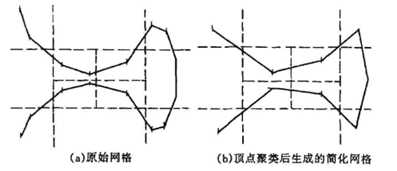
令为每个与顶点集合V相关的三角形集合T(V)中的三角形所在平面的平面方程，且有。此计算方法同QEM算法的二次误差测度。

改进后效果

算法选型

通过上述算法原理的介绍和分析，结合OpenSceneGraph的分页加载数据库的机制，在网格模型的呈现上我们使用离线LOD的加载方式，预处理网格模型。使用预处理网格模型简化的原因由几个方面：

1. 离线LOD的数据组织简单；
2. 需要利用预处理简化模型在磁盘上的存储作资源管理；
3. 以地球为三维场景显示时，不同简化程度网格模型在变化过程中的跳跃感不明显，几乎可以忽略不记；
4. 需要保证场景操作的性能，离线LOD的方式比较合适。

VTK的网格简化算法

VTK(Visualization Toolkit)开发包中包含了基于传统二次误差测度的QEM和顶点聚类算法，对于VTK的QEM算法实现代码和效果：

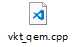
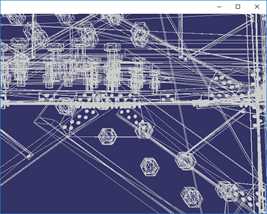
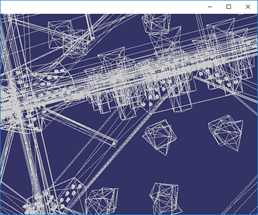
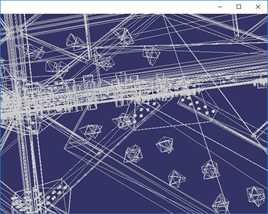
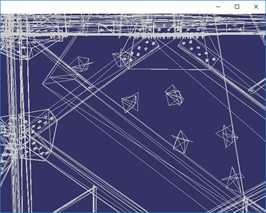
按上图顺序，简化程度数据如下：

简化目标(%)	100%	50%	25%	12.5%
三角面数	675460	337730	168864	84431
顶点数	380869	212013	128587	85527
时间(ms)	0ms	2051ms	1950ms	1842ms

 

VCG的网格简化算法

    VCGLib(Visualization and Computer Graphics Library)是一套开源的、便携的C++模板库，提供三维图形和网格操作功能。VCG中提供了一系列的网格简化算法，主要使用的有两种，一种是基于QEM的网格简化算法，另一种是基于CLIQUE的顶点聚类网格简化算法。基于QEM的简化算法效果如下：

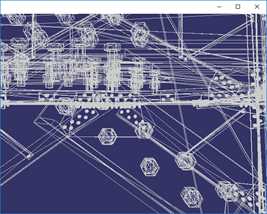
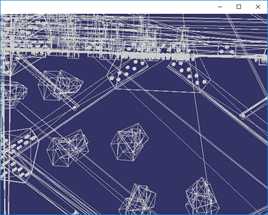
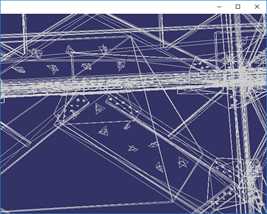
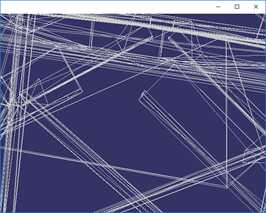
按上图顺序，简化程度数据如下：

简化目标(%)	100%	50%	12.5%	1.5%
三角面数	675460	337730	84432	6739
顶点数	380869	212031	64033	10554
时间(ms)	0ms	2252ms	1530ms	920ms

 

顶点聚类算法简化效果如下:

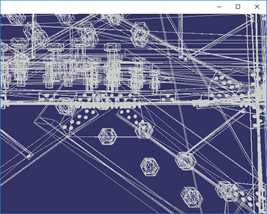
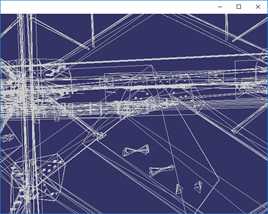
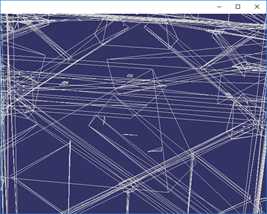
按上图顺序，简化程度数据如下：

简化目标(%)	100%	16%	5%	3%
三角面数	675460	112058	35271	21081
顶点数	380869	65488	21690	13042
时间(ms)	0ms	910ms	431ms	389ms

 

基于QEM的改进算法

来自https://github.com/lvweiwolf/Fast-Quadric-Mesh-Simplification.git的改进简化算法，基于QEM改进。大体思路与QEM是一致的，在实现上做了优化。该算法据说是Meshlab的4倍，Meshlab使用的就是VCGLib的简化算法，目前没有实际测试数据，效果如下：