拓扑排序的 +Leapms 线性规划模型
Posted leapms
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了拓扑排序的 +Leapms 线性规划模型相关的知识,希望对你有一定的参考价值。
知识点
拓扑排序
拓扑排序的+Leapms模型
无圈有向图
一个图G(V,E), 如果边有向且不存在回路,则为无圈有向图。在无圈有向图上可以定义拓扑排序。下图是一个无圈有向图的例子。
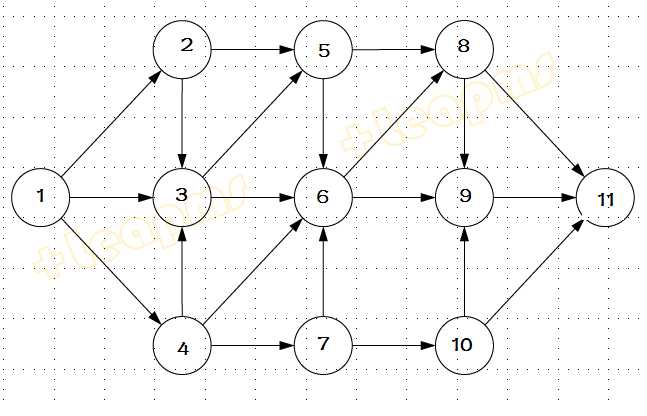
拓扑排序
给定一个无圈有向图G(V,E),对其顶点集合V中的元素进行排序,使得对任何两个顶点v1,v2,如果(v1,v2)是图上的一条边,则在排序中v1优先于v2.
拓扑排序的+Leapms模型
对图G(V,E)中的边的表示可以用其起始边和终止边表示,对第k条边,其起始定点使用函数alpha[k]表示,其终止顶点用beta[k]表示。
设m是图中的边数,n是图中的顶点数。设x[i]是顶点i的次序数(拓扑排序中允许并列次序,例如并列第2等等)。
于是对任意一条边,其终止顶点的次序数一定至少比其起始顶点的次序数大至少1。于是有约束:
x[bata[k]]>=x[alpha[k]]+1 | k=1,...,m
希望至少从1开始编号次序数,于是有另外的约束:
x[i]>=1|i=1,...,n
为了对次序数进行紧凑编号,模型的目标设为极小化所有次序数的和:
min sum{i=1,...,n}x[i]
完整的+Leapms模型为:
min sum{i=1,...,n}x[i]
subject to
x[bata[k]]>=x[alpha[k]]+1 | k=1,...,m
x[i]>=1|i=1,...,n
where
m,n are integers
e is a set
alpha[k],bata[k] are integers| k=1,...,m
x[i] is a variable of nonnegative number| i=1,...,n
data_relation
m=_$(e)/2
alpha[k]=e[2k-1] | k=1,...,m
bata[k]=e[2k] | k=1,...,m
n=0
n=max(n,alpha[k]) | k=1,...,m
n=max(n,bata[k]) | k=1,...,m
data
e={
(1 2)
(1 3)
(1 4)
(2 3)
(2 5)
(3 5)
(3 6)
(4 6)
(4 7)
(5 6)
(5 8)
(6 8)
(6 9)
(7 6)
(7 10)
(8 9)
(8 11)
(9 11)
(10 9)
(10 11)
}
求解过程:
+Leapms>load
Current directory is "ROOT".
.........
toposort.leap
.........
please input the filename:toposort
================================================================
1: // x[i] 是 i点的拓扑排序层次
2:
3: min sum{i=1,...,n}x[i]
4: subject to
5: x[bata[k]]>=x[alpha[k]]+1 | k=1,...,m
6: x[i]>=1|i=1,...,n
7:
8: where
9: m,n are integers
10: e is a set
11: alpha[k],bata[k] are integers| k=1,...,m
12: x[i] is a variable of nonnegative number| i=1,...,n
13:
14: data_relation
15: m=_$(e)/2
16: alpha[k]=e[2k-1] | k=1,...,m
17: bata[k]=e[2k] | k=1,...,m
18: n=0
19: n=max(n,alpha[k]) | k=1,...,m
20: n=max(n,bata[k]) | k=1,...,m
21:
22: data
23: e={
24: (1 2)
25: (1 3)
26: 1 4
27: 2 3
28: 2 5
29: 3 5
30: 3 6
31: 4 6
32: 4 7
33: 5 6
34: 5 8
35: 6 8
36: 6 9
37: 7 6
38: 7 10
39: 8 9
40: 8 11
41: 9 11
42: 10 9
43: 10 11
44: }
================================================================
>>end of the file.
Parsing model:
1D
2R
3V
4O
5C
6S
7End.
..................................
number of variables=11
number of constraints=31
..................................
+Leapms>mip
relexed_solution=45; number_of_nodes_branched=0; memindex=(2,2)
The Problem is solved to optimal as an MIP.
找到整数规划的最优解.非零变量值和最优目标值如下:
.........
x1* =1
x2* =2
x3* =3
x4* =2
x5* =4
x6* =5
x7* =3
x8* =6
x9* =7
x10* =4
x11* =8
.........
Objective*=45
.........
+Leapms>
标记在图上
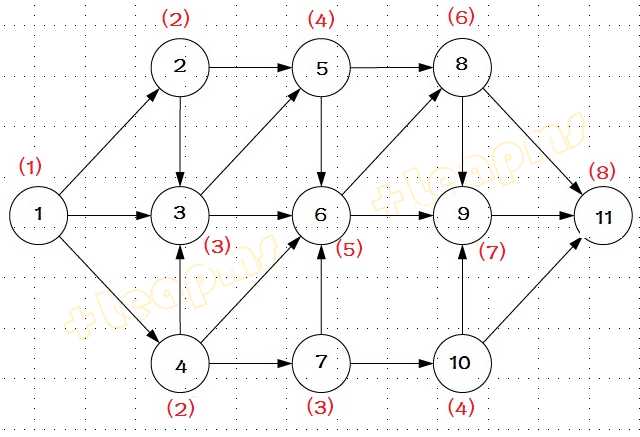
拓扑排序的用途
拓扑排序在算法设计上有广泛的用途,例如在制造资源管理中的Gozinto图的计算等。
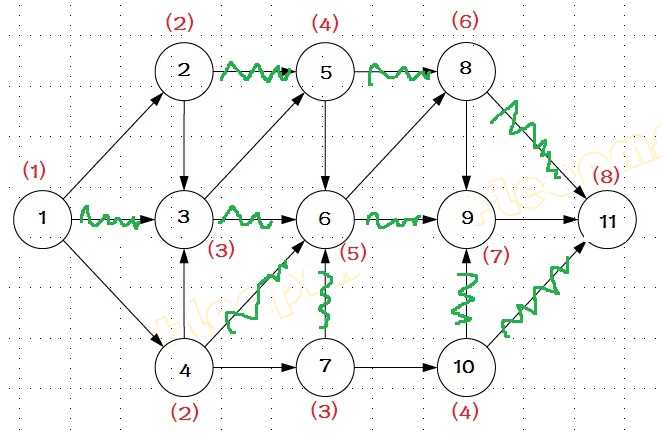
对上述图如果有向边表示次序关系,则可删除任何起始顶点和终止顶点次序数相差大于2的边得到更加简化的图,且不改变次序逻辑:
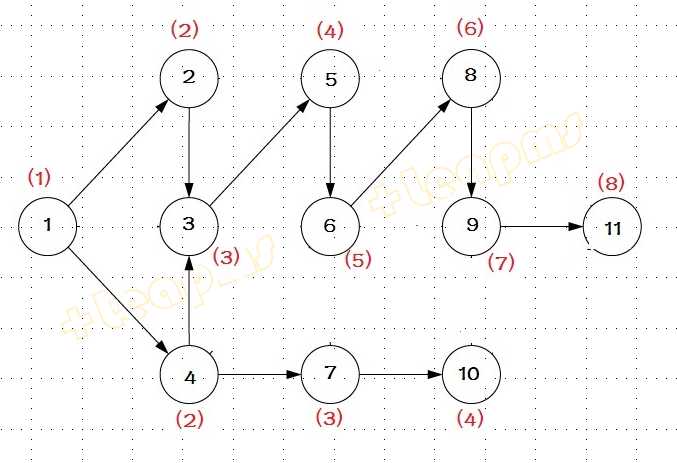
以上是关于拓扑排序的 +Leapms 线性规划模型的主要内容,如果未能解决你的问题,请参考以下文章