知识点总结报告 2.1

Posted 2020-10-23 desier

---恢复内容开始---

　　知识点：简单二叉树的前序创建以及三种基本遍历

　　二叉树：极其重要的数据结构之一，一个node节点包含一个数据域，两个指针域，这两个指针域分别向下指向它的左儿子，右儿子，而左右儿子又是一个节点，同样指向他们的左儿子、右儿子……二叉树与链表有类似之处，大家别看我们在纸上画的树的图节点之间是用线连起来的，但是实际上每个节点在内存中的空间分配是不连续的，因为它是随机的，通过跟进调试配合watches窗口配合观察就能发现这一点。二叉树的创建函数和遍历函数都是递归函数，因此要写好退出函数的条件不然就一直递归下去了。

　　对于二叉树，初学者可以先从网上拷贝一段可执行的清楚地代码，通过调试，一步一步地看，一步一步地想，不然，很难想懂很花时间

　　二叉树的定义：二叉树

typedef struct BiTNode
{
    char data;
    struct BiTNode *leftchild;
    struct BiTNode *rightchild;
}BiTNode,*BiTree;//注意这里的 BiTNode等于*BiTree,注意*号,BiTree是一个类型名， BiTree T,声明的是一个基类型为BiTNode的指针T，BiTree *T则是把*T看成是指针，T是这个指针的地址

　　二叉树的前序创建：先设置好中断递归的条件（层层递归一次中断是跳不出去的）

void createBiTree(BiTree *T)
{
    char ch;
    ch=getchar();
    if(ch==‘#‘)
    {
        *T=NULL;
    }
    else
    {
        *T=(BiTree)malloc(sizeof(BiTNode));
        (*T)->data=ch;
        createBiTree(&(*T)->leftchild);
        createBiTree(&(*T)->rightchild);
    }
}

　　二叉树的前、中、后序遍历：前序遍历就是先遍历根节点再根节点的左儿子这边，最后遍历根节点的右儿子这边；中序遍历就是中间才遍历根节点；后序遍历就是最后遍历根节点。

void operation(char ch,int n)
{
    printf("这个字母是：%c,他在第%d层\\n",ch,n);
}

void PreOrderTraverse(BiTree T,int level)
{
    if(T==NULL)
    {
        return ;
    }
    operation(T->data,level);
    PreOrderTraverse(T->leftchild,level+1);
    PreOrderTraverse(T->rightchild,level+1);
}

void InOrderTraverse(BiTree T,int level)
{
    if(T==NULL)
    {
        return ;
    }
    InOrderTraverse(T->leftchild,level+1);
    operation(T->data,level);
    InOrderTraverse(T->rightchild,level+1);
}

void PostOrderTraverse(BiTree T,int level)
{
    if(T==NULL)
    {
        return ;
    }
    PostOrderTraverse(T->leftchild,level+1);
    PostOrderTraverse(T->rightchild,level+1);
    operation(T->data,level);
}

接下来是主函数：

int main()
{
    int levell=1;
    BiTree TREE=NULL;
    printf("请按照前序输出：\\n");
    createBiTree(&TREE);
    printf("前序输出结果：\\n");
    PreOrderTraverse(TREE,levell);
    printf("中序输出结果：\\n");
    InOrderTraverse(TREE,levell);
    printf("后序输出结果：\\n");
    PostOrderTraverse(TREE,levell);
    return 0;
}

在运行代码时不要随意写上测试用例，不然很可能得不出输出，因为创建函数这个递归函数还没有跳出去。因此写测试用例时要先在纸上把图画好，正确的输入。

比如我们画出来得二叉树图是这样的：

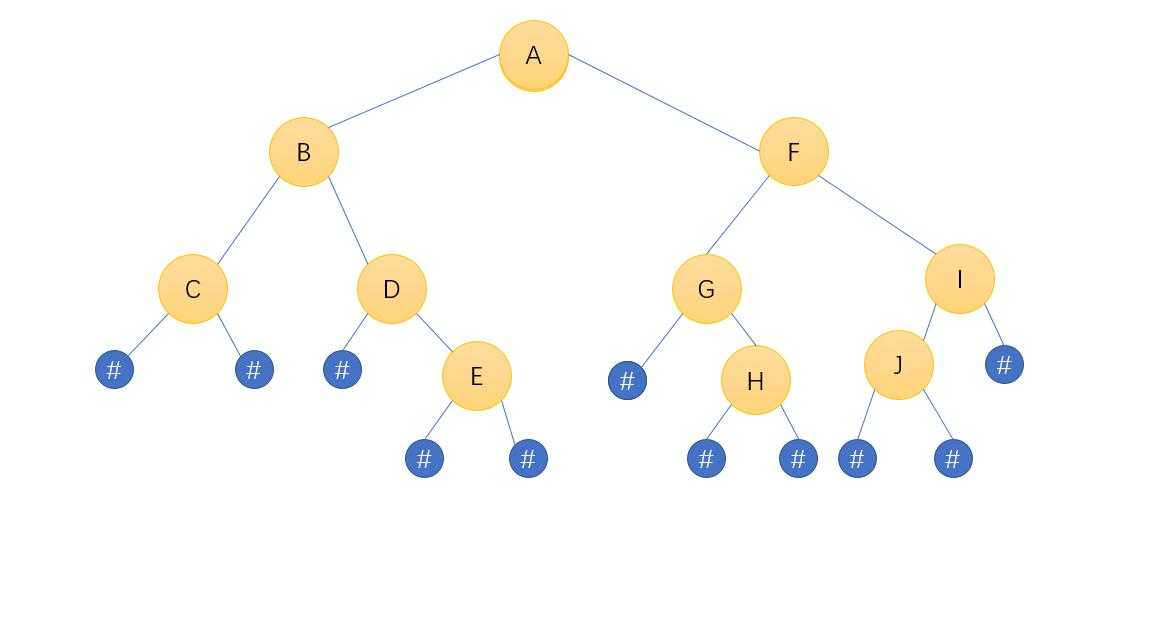
那么按照前序输入格式，我们应该这样输入：ABC##D#E##FG#H##IJ###

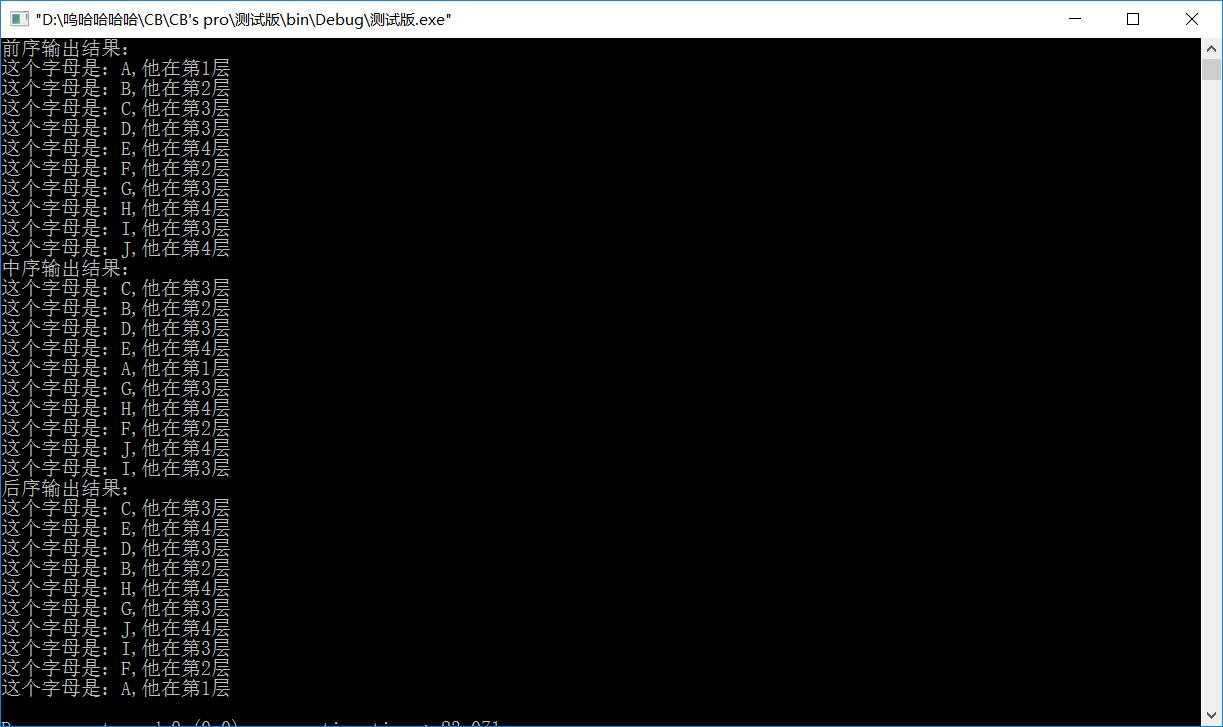
得到的结果是这样的：