浅谈普通莫队算法

Posted 2021-01-24 neworld2002

前言

• 对于一个维护区间的问题，最暴力的方法就是每次枚举区间，进行统计。
• 而这就是莫队的基本思路
• 但不过莫队的枚举是进行优化的，可以优化到(O(Nsqrt{N}))

基本思路

• 首先：已知([L,R])的答案，那么求([L-1,R]) 、([L+1,R]) 、([L,R-1])、([L,R+1])的代价为(O(1))
• 如果你已知区间([L,R])的答案，那么对于区间([l,r])，如果两个区间有交集，那么这个交集就没有必要再去计算了，所以我们只需要移动端点即可。
• 但是代价还是(O(N^2))
• 我们考虑将所有访问的左端点进行排序
• 并按照左端点分类的，变成一块一块的，块的长度为(len)

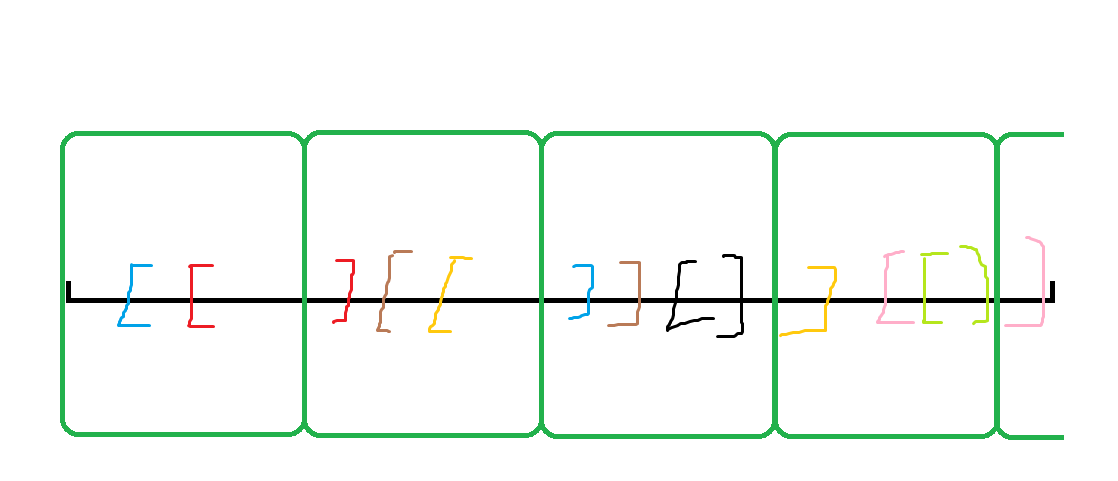
• 你会发现左端点在同一个块内的询问，经过排序后一定会在一起（很显然啊……）
• 于是我们就想，如果对于一个块的操作，按照右端再排一次序，
• 这样左端点移动的次数一定不超过(len)，右端点移动次数总和最大是(N)
• 举个例子：

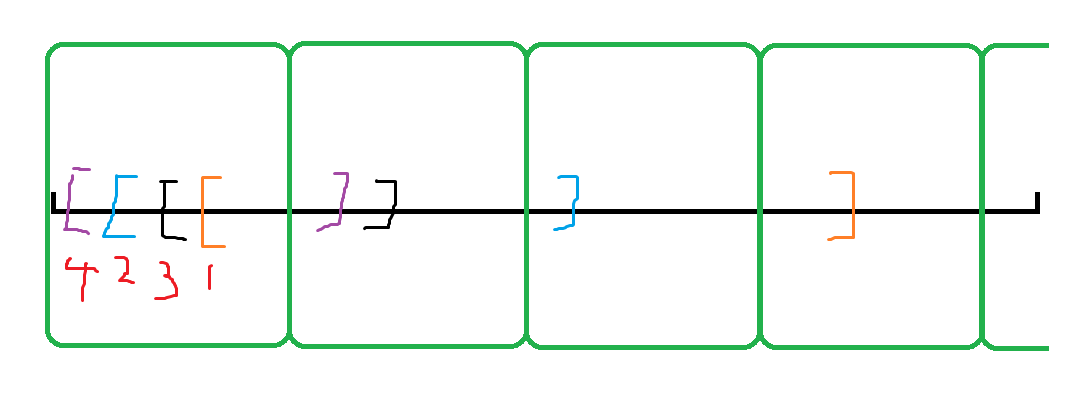
• 很显然的是，左端点的移动肯定在这个块内，而块的大小为(len)，所以每次移动的代价为(len)
• 并且这个块内是按照右端点排序的。（这里采用从大到小）
• 所以一开始右端点统计的是橙色区间
• 接下来统计蓝色区间，右端点左移
• 统计黑色区间，右端点左移
• 统计紫色区间，右端点左移
• 诶你会发现在同一个块内，右端点的移动一定是单向的！！
• 所以处理一个块的右端点移动，最多是(N)次
• 并且处理下一个块的时候，我们可以从小到大排序，这样右端点就可以从左边直接移到右边
• 再下一个块的时候从大到小，有端点就是从右到左了

时间复杂度

• 一共(M)次询问，一共(frac{N}{len})个块
• 对于每次询问，左端点移动代价为(len)，所以是(M imes len)
• 对于一个块，右端点移动代价为(N)，所以是(frac{N}{len} imes N)
• (N,M)同级，所以总代价为$N imes len + frac{N}{len} imes N= N(len+frac{N}{len}) $
• 好像是个对勾函数诶！也就是基本不等式了
• (len+frac{N}{len} leq 2sqrt{frac{N}{len}*len})
• 所以(N(len+frac{N}{len} )leq 2Nsqrt{N})
• 时间复杂度为(O(Nsqrt{N}))

code

• 传送门
• 处理区间不同的数字个数
• 开个桶去算就行了

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#define MAXN 20005

struct Node {
    int l,r,num,ans;
}G[MAXN];

struct io {
    char ibuf[1 << 25] , *s;
    io() {
        fread( s = ibuf , 1 , 1 << 25 , stdin);
    }
    inline int read() {
        int u = 0, v = 1;
        while( *s < 48) v = * s++ ^ 45 ? 1 : -1;
        while(*s > 32) u = u * 10 + *s++ - 48;
        return u*v;
    }
}ip;
#define read ip.read

int cur[MAXN],book[1000005],rec[MAXN];
int N,M,size,count = 0;

inline void up(int u) {
    book[cur[u]] ++;
    if(book[cur[u]]==1) count ++;
}

inline void down(int u) {
    book[cur[u]] --;
    if(book[cur[u]]==0) count --;    
}

inline bool cmp(Node a,Node b) {
    return (a.l/size)^(b.l/size) ? a.l < b.l : ( (a.l/size)&1 ? a.r < b. r : a.r > b.r);
}

int main() {

    N = read();
    size = floor(sqrt(N));
    for(int i=1;i<=N;++i) {
        cur[i] = read();
    }
    M = read();
    std::memset(book,0,sizeof(book));
    
    for(int i=1;i<=M;++i) {
        G[i].l = read(); G[i].r = read(); G[i].num = i;
    }
    std::sort(G+1,G+M+1,cmp);

    int L = G[1].l , R = G[1].r;
    for(int i=L;i<=R;++i) up(i);
    for(int i=1;i<=M;++i) {
        rec[G[i].num] = i;
        while(R<G[i].r) up(++R);
        while(L<G[i].l) down(L++);
        while(L>G[i].l) up(--L);
        while(R>G[i].r) down(R--);
        G[i].ans = count;
    }

    for(int i=1;i<=M;++i) printf("%d
",G[rec[i]].ans);
    return 0;
}