LeetCode 2373. 矩阵中的局部最大值

Posted 2023-03-09 Tisfy

【LetMeFly】2373.矩阵中的局部最大值

力扣题目链接：https://leetcode.cn/problems/largest-local-values-in-a-matrix/

给你一个大小为 n x n 的整数矩阵 grid 。

生成一个大小为 (n - 2) x (n - 2) 的整数矩阵  maxLocal ，并满足：

• maxLocal[i][j] 等于 grid 中以 i + 1 行和 j + 1 列为中心的 3 x 3 矩阵中的 最大值 。

换句话说，我们希望找出 grid 中每个 3 x 3 矩阵中的最大值。

返回生成的矩阵。

 

示例 1：

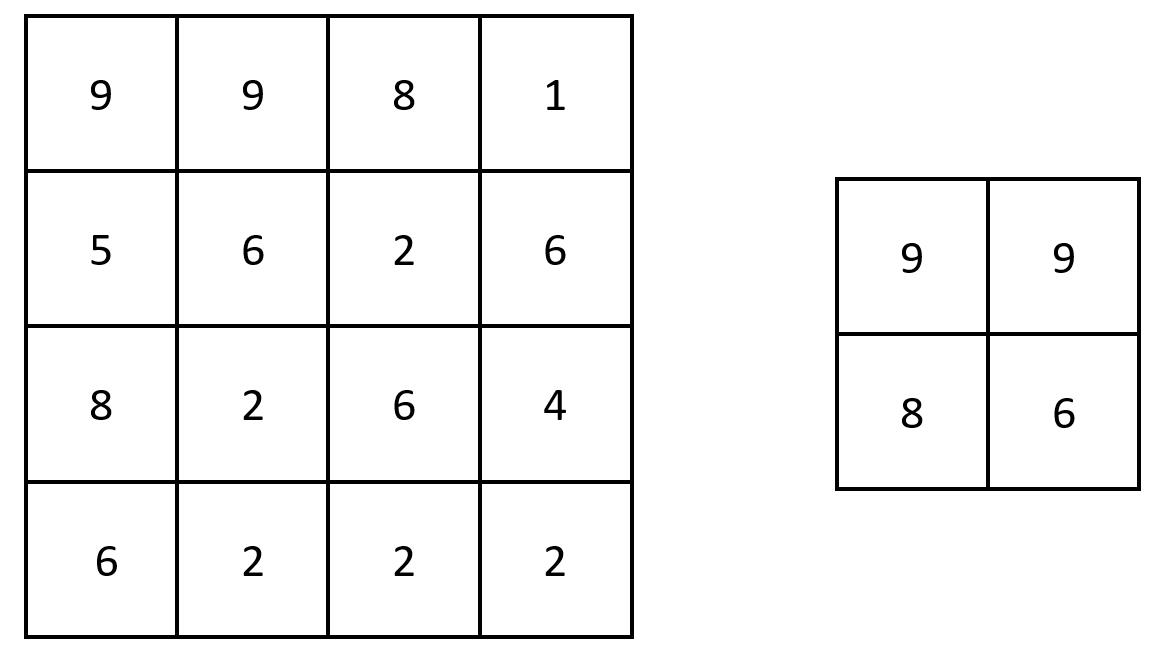
输入：grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]
输出：[[9,9],[8,6]]
解释：原矩阵和生成的矩阵如上图所示。
注意，生成的矩阵中，每个值都对应 grid 中一个相接的 3 x 3 矩阵的最大值。

示例 2：

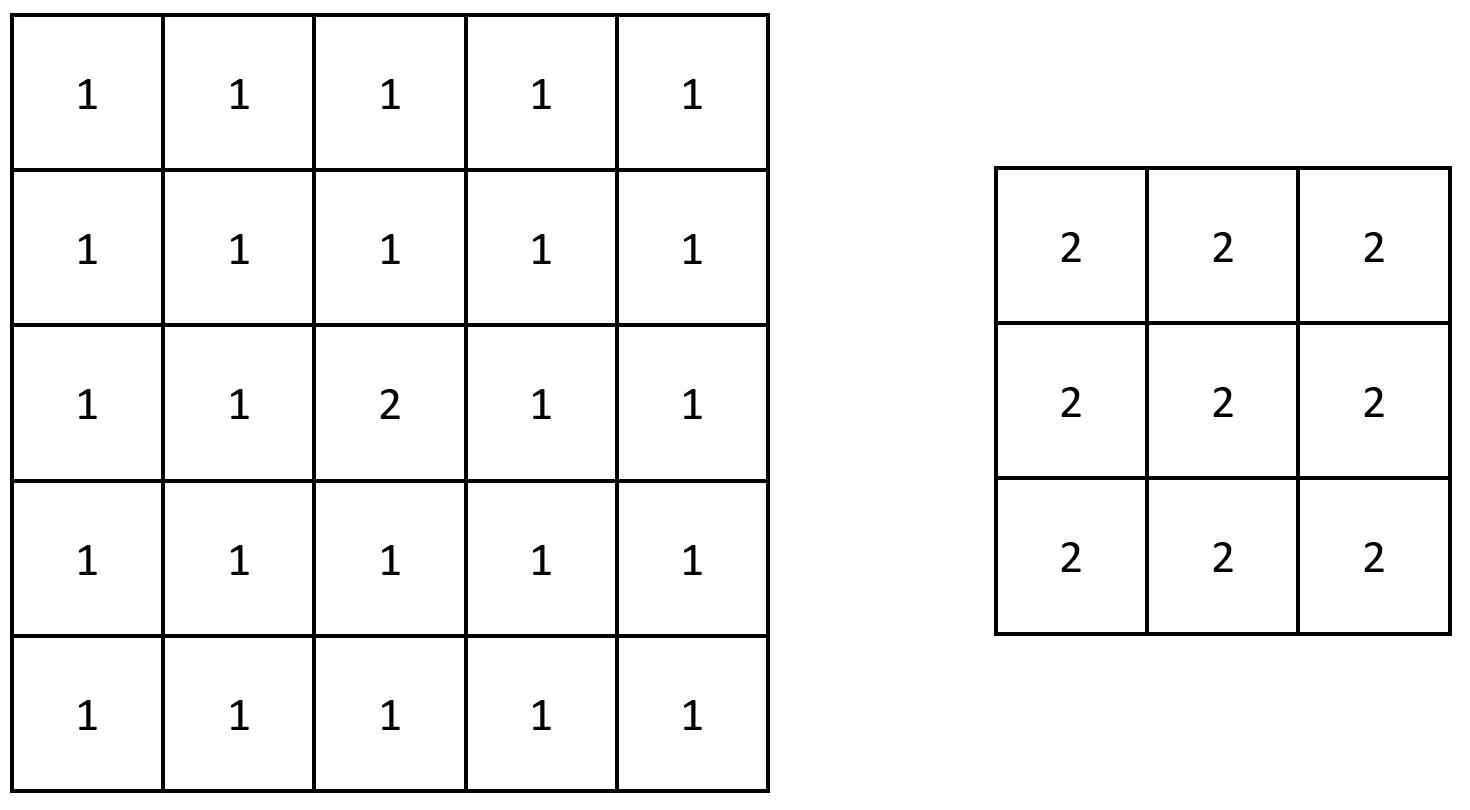
输入：grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]
输出：[[2,2,2],[2,2,2],[2,2,2]]
解释：注意，2 包含在 grid 中每个 3 x 3 的矩阵中。

 

提示：

• n == grid.length == grid[i].length
• 3 <= n <= 100
• 1 <= grid[i][j] <= 100

方法一：模拟

假设grid的size为$n\times n$，那么答案的size就为$(n-2)\times (n-2)$

先生成这么大的空数组，然后遍历答案数组的每一个位置在原始数组中对应的$3\times 3$矩阵的中心，对于每个位置，求出其$3\times 3$矩阵的最大值即可

• 时间复杂度$O(len(grid{)}^2)$
• 空间复杂度$O(1)$，力扣算法返回值不计入算法的空间复杂度

AC代码

C++

class Solution 
public:
    vector<vector<int>> largestLocal(vector<vector<int>>& grid) 
        int n = grid.size();
        vector<vector<int>> ans(n - 2, vector<int>(n - 2));
        for (int i = 1; i + 1 < n; i++) 
            for (int j = 1; j + 1 < n; j++) 
                int M = 1;
                for (int k = -1; k <= 1; k++) 
                    for (int l = -1; l <= 1; l++) 
                        M = max(M, grid[i + k][j + l]);
                    
                
                ans[i - 1][j - 1] = M;
            
        
        return ans;
    
;

Python

class Solution:
    def largestLocal(self, grid: List[List[int]]) -> List[List[int]]:
        n = len(grid)
        ans = [[0 for _ in range(n - 2)] for __ in range(n - 2)]
        for i in range(1, n - 1):
            for j in range(1, n - 1):
                M = 1
                for k in range(-1, 2):
                    for l in range(-1, 2):
                        M = max(M, grid[i + k][j + l])
                ans[i - 1][j - 1] = M        
        return ans

语法糖简化：

class Solution:
    def largestLocal(self, grid: List[List[int]]) -> List[List[int]]:
        n = len(grid)
        ans = [[0 for _ in range(n - 2)] for __ in range(n - 2)]
        for i in range(1, n - 1):
            for j in range(1, n - 1):
                ans[i - 1][j - 1] = max(grid[x][y] for x in range(i - 1, i + 2) for y in range(j - 1, j + 2))
        return ans

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/129274862