递归控制-列出所有组合

Posted 2021-01-23 pylearn

0.目录

1.递归思路

2.Java代码实现

• 2.1 分开考虑初始值
• 2.2 合并各自初始条件
• 2.3 维护side-effect
• 2.4 测试用例

1.递归思路

列出所有组合，例如从1,2,3,4中任取2个元素，求出所有的组合。

面对combinations([1,2,3,4], 2):
递归思路为：

• 选1 → combinations([2,3,4], 1)

• 不选1 → combinations([2,3,4], 2)

  2.Java代码实现

  2.1 分开考虑初始值

  先分开考虑传入参数的初始值

    /**
     * Generates all combinations and output them,
     * selecting n elements from data
     */
    public void combinations(List<Integer> data, int n) {
        // initial value for recursion
        if (data.isEmpty()) {
            if (n == 0) {
                // output empty list
            }
            return;
        }

        if (n < 0) {
            return;
        }

        if (n == 0) {
            // output empty list
            return;
        }

        // select element 0
        combinations(data.subList(1, data.size()), n - 1);

        // un-select element 0
        combinations(data.subList(1, data.size()), n);
    }

2.2 合并各自初始条件

合并初始值条件后，考虑两个问题：
如何选择元素？如何输出？

    /**
     * Generates all combinations and output them,
     * selecting n elements from data
     */
    public void combinations(List<Integer> data, int n) {
        // how to select elements
        // how to output

        if (n == 0) {
            // output all selected elements
            return;
        }

        if (data.isEmpty()) {
            // output empty list
            return;
        }

        // select element 0
        combinations(data.subList(1, data.size()), n - 1);

        // un-select element 0
        combinations(data.subList(1, data.size()), n);
    }

2.3 维护side-effect

维护一个selected，也就是之前所选择的的所有元素。

    /**
     * Generates all combinations and output them,
     * selecting n elements from data
     */
    public void combinations(
        List<Integer> selected, List<Integer> data, int n) {
        if (n == 0) {
            // output all selected elements
            for (Integer i : selected) {
                System.out.print(i);
                System.out.print(" ");
            }
            System.out.println();
            return;
        }

        if (data.isEmpty()) {
            // output empty list
            return;
        }

        // select element 0
        selected.add(data.get(0));
        combinations(selected, data.subList(1, data.size()), n - 1);

        // un-select element 0
        selected.remove(selected.size() - 1);
        combinations(selected, data.subList(1, data.size()), n);
    }

2.4 测试用例

测试程序是否正确运行：

    public static void main(String[] args) {
        Combinations comb = new Combinations();
        comb.combinations(
            new ArrayList<>(), Arrays.asList(1, 2, 3, 4), 2);
    }

运行结果为

多测几个极端用例

    public static void main(String[] args) {
        Combinations comb = new Combinations();
        comb.combinations(
            new ArrayList<>(), Arrays.asList(1, 2, 3, 4), 2);
        System.out.println("=================");
        comb.combinations(
            new ArrayList<>(), Arrays.asList(), 2);
        System.out.println("=================");
        comb.combinations(
            new ArrayList<>(), Arrays.asList(), 0);
        System.out.println("=================");
        comb.combinations(
            new ArrayList<>(), Arrays.asList(1, 2, 3, 4), 1);
        System.out.println("=================");
        comb.combinations(
            new ArrayList<>(), Arrays.asList(1, 2, 3, 4), 0);
        System.out.println("=================");
    }

运行结果为

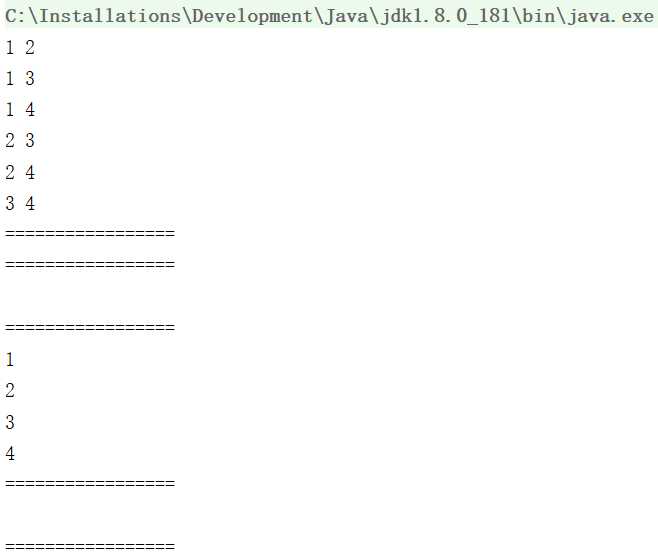
全部代码：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class Combinations {

    /**
     * Generates all combinations and output them,
     * selecting n elements from data
     */
    public void combinations(
        List<Integer> selected, List<Integer> data, int n) {
        if (n == 0) {
            // output all selected elements
            for (Integer i : selected) {
                System.out.print(i);
                System.out.print(" ");
            }
            System.out.println();
            return;
        }

        if (data.isEmpty()) {
            // output empty list
            return;
        }

        // select element 0
        selected.add(data.get(0));
        combinations(selected, data.subList(1, data.size()), n - 1);

        // un-select element 0
        selected.remove(selected.size() - 1);
        combinations(selected, data.subList(1, data.size()), n);
    }

    public static void main(String[] args) {
        Combinations comb = new Combinations();
        comb.combinations(
            new ArrayList<>(), Arrays.asList(1, 2, 3, 4), 2);
        System.out.println("=================");
        comb.combinations(
            new ArrayList<>(), Arrays.asList(), 2);
        System.out.println("=================");
        comb.combinations(
            new ArrayList<>(), Arrays.asList(), 0);
        System.out.println("=================");
        comb.combinations(
            new ArrayList<>(), Arrays.asList(1, 2, 3, 4), 1);
        System.out.println("=================");
        comb.combinations(
            new ArrayList<>(), Arrays.asList(1, 2, 3, 4), 0);
        System.out.println("=================");
    }
}