划分树（poj2104）

Posted 2021-01-23 cglongge

poj2104

题意：给出n个数，有m次查询，每次查询要你找出 l 到 r 中第 k 大的数；

思路：划分树模板题

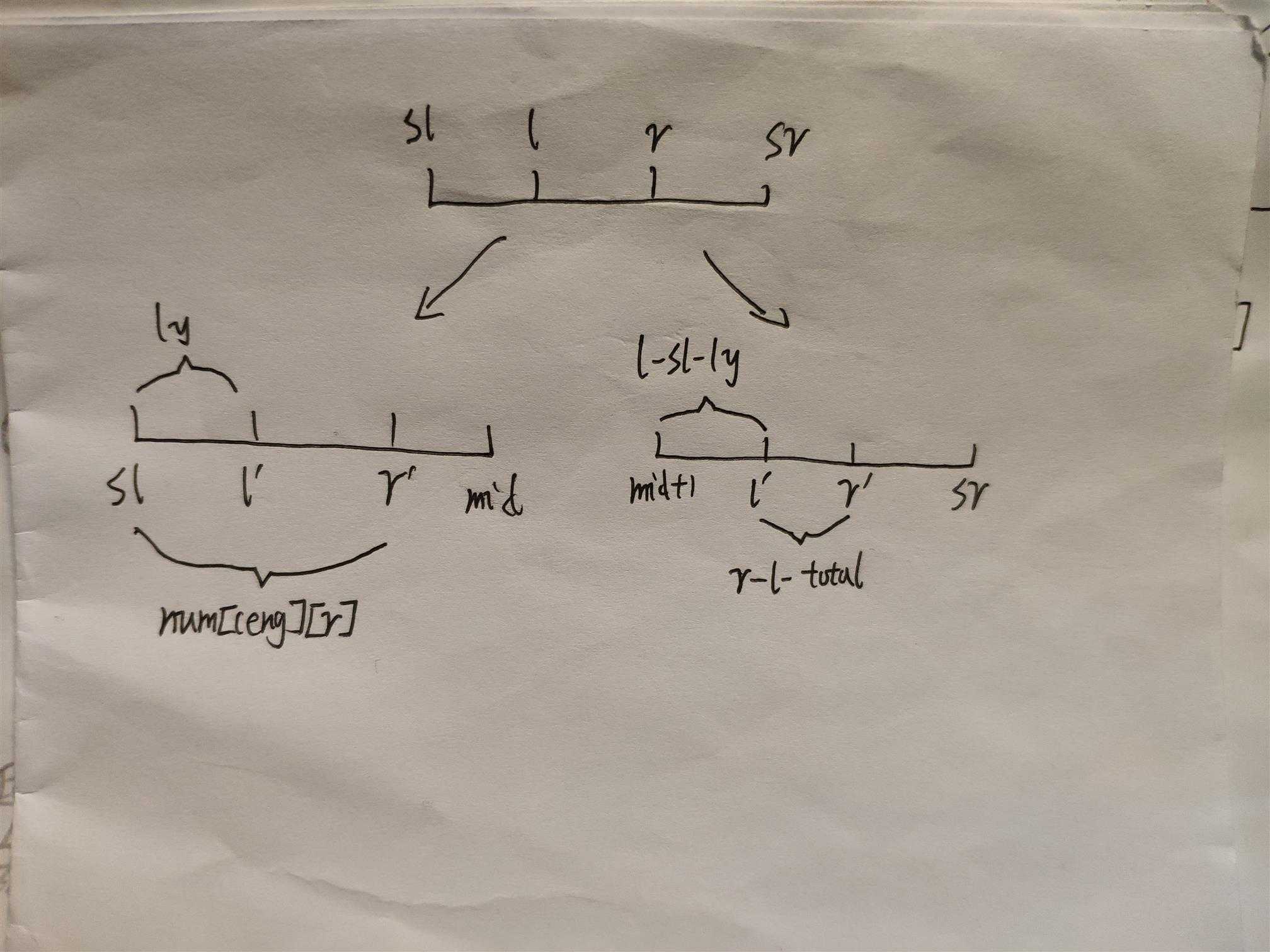
上述图片展现了查询时如何往下递推的过程

其中ly表示 [sl,l) 中有多少个数进入了左子树，num[ceng][r]表示[sl,r]中有多少个数进入了左子树，total表示[l,r]中有多少个数进入了左子树。

代码：

#include<cstdio> 
#include<algorithm>
using namespace std;
int s[20][100010];
int st[100010];//排序后的数组 
int num[20][100010];//第i层前j个数有几个进入了左子树 
void bt(int ceng,int l,int r){
    if(l==r)//递归到l，r相等时 
    return;
    int mid=(l+r)/2;
    int sum1=mid-l+1;  
    for(int i=l;i<=r;i++){//计算该有多少个与中间值相等的数可以进入左子树 
        if(s[ceng][i]<st[mid])
        sum1--;
    }
    int cnt1=0,cnt2=1;
    for(int i=l;i<=r;i++){
        if(i==l){
            num[ceng][i]=0;
        }
        else{
            num[ceng][i]=num[ceng][i-1];
        }
        
        if(s[ceng][i]<st[mid]||s[ceng][i]==st[mid]&&sum1>0){//如果当前数字小于中间数或者当前数等于中间数并且当前进入左子树并与中间数相等的数的数量小于限制数量时 
            int k1=l+cnt1++;
            //printf("qqqq%d %d %d
",ceng,cnt1,k1);
            s[ceng+1][k1]=s[ceng][i];
            num[ceng][i]++;
            if(s[ceng][i]==st[mid])//如果相等，则与中间数相等的数可以进入的位置又少了一个 
            sum1--;
        }
        else{//进入右子树 
            int k2=mid+cnt2++;
            s[ceng+1][k2]=s[ceng][i];
            //printf("qqqq%d %d %d
",ceng,cnt2,k2);
        }
    }
    bt(ceng+1,l,mid);//递归建树 
    bt(ceng+1,mid+1,r);    
}
int query(int ceng,int sl,int sr,int l,int r,int k){
    //printf("www%d %d %d
",ceng,sl,sr);
    if(sl==sr){//递归到叶子节点 
        //printf("qq%d %d %d
",ceng,sl,s[ceng][sl]);
        return s[ceng][sl];
    }
    int ly;
    if(l==sl)
    ly=0;//ly代表该段的l前面有多少个数进入了左子树 
    else
    ly=num[ceng][l-1];
    int total=num[ceng][r]-ly;//l到r之间有多少个数进入了左子树 
    if(total>=k){//该区间有大于k个数进入了左子树 ，则第k大的数一定在左子树里面 
        return query(ceng+1,sl,(sl+sr)>>1,sl+ly,sl+num[ceng][r]-1,k);
        //l=sl+ly;新的左范围等于边界sl+l前面的数进入左子树的个数 
        //r=sl+num[ceng][r]-1;新的右范围等于边界sl+前r个数中进入左子树的个数 
    } //为什么r！=sl+ly +  k因为虽然连续，但不是有序的 
    else{
        int lr=l-sl-ly+((sl+sr)>>1)+1;//新的左范围等于l前面的数的总数减去前面数进入左子树的个数加上右子数的开始位置 
        return query(ceng+1,((sl+sr)>>1)+1,sr,lr,lr+r-l-total,k-total);
        //新的右范围等于新的左范围加上l到r之间数的个数减去l和r之间的数进入左子树的个数 
    }
     
}
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%d",&s[0][i]);
        st[i]=s[0][i];
    }
    sort(st+1,st+n+1);
    bt(0,1,n);
    while(m--){
        int l,r,k;
        scanf("%d%d%d",&l,&r,&k);
        printf("%d
",query(0,1,n,l,r,k));
    }
    return 0;
}