线性回归.1

Posted 2021-01-22 fromzore

机器学习分为有监督学习和无监督学习。

有监督学习分为回归问题和分类问题。

Regression 回归问题是指我们想要预测连续的数值输出

Classification 分类是指我们设法预测一个离散值输出（0 or 1），有时也可以存在有两个以上的可能的输出值。

 

设有一组数据，x为自变量，y为因变量，(x(i),y(i))代表一组数据。

我们想要预测y，则设hθ(x(i))=θ_0+θ_1x(i)

那么这个单变量线性回归的代价函数为J(θ_0,θ_1)=1/2m   m∑i=1 (hθ(x(i))-y(i))^2   就是用预测的减去实际的，然后让他俩的平方和尽可能的小

我们要做的就是关于θ_0和θ_1对函数J(θ_0,θ_1)求最小值，这就是我们的代价函数也被称作平方误差函数。

既然要求θ_0和θ_1,就要用到梯度下降算法：

1.对θ_0,θ_1初始化，一般设为θ_0=0,θ_1=0;

2.一点点改变θ_0,θ_1的值，来使J(θ_0,θ_1)变小，直到我们找到最小或局部最小值

所以，一直进行以下这个公式，直到收敛。θj=θj-α(d/dθj)J(θ_0,θ_1)所有的θ同步更新

α是学习率，为常数量，控制梯度下降时我们迈出多大的步子（控制多大幅度的更新）α的值多为0.01,0.005，python中有其默认值

更新：正确方法：temp0=θ_0-α(d/dθ_0)J(θ_0,θ_1)      是的，我们要做到同步更新

                            temp1=θ_1-α(d/dθ_1)J(θ_0,θ_1)

                            θ_0=temp0

                            θ_1=temp1

 

梯度下降时没有必要再另外减小α，因为随着梯度下降，导数会变小，更新的幅度也会变小

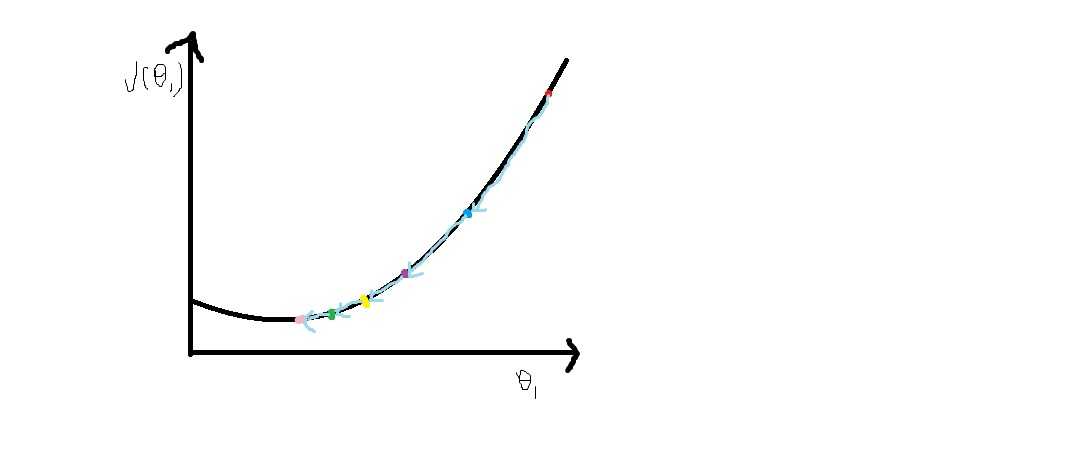
对公式(d/dθj)J(θ_0,θ_1)进行计算

α(d/dθj)J(θ_0,θ_1)=α(d/dθj)  1/2m   m∑i=1 (hθ(x(i))-y(i))^2=α(d/dθj)  1/2m   m∑i=1 (θ_0+θ_1(x(i))-y(i))^2

带入梯度下降公式得，求的θ_0，θ_1得方法

repeat until convergence{

θ_0=θ_0-α  1/m   m∑i=1 (hθ(x(i))-y(i))

θ_1=θ_1- α 1/m   m∑i=1 (hθ(x(i))-y(i)) x(i)

}