莫队详解

Posted 2021-01-21 yzhang-rp-inf

莫队实际很简（du）单（liu）

依照某位dalao的说法，就是两只小手（two-pointers）瞎跳

莫队

我们以Luogu P3901 数列找不同为例讲一下静态莫队

这道题是个绿题，因为数据比较弱，但真是一道良心的莫队练手题

莫队是由前国家队队长莫涛发明的

莫队算法的精髓就是通过合理地对询问排序，然后以较优的顺序暴力回答每个询问。处理完一个询问后，可以使用它的信息得到下一个询问区间的答案。（两个小手瞎跳）

考虑这个问题：对于上面这道题，我们知道区间[1,5]每个数的数量，如何求出[2,6]每个数的数量

算法1：暴力扫一遍（废话）

算法2：珂以在区间[1,5]的基础上，去掉位置1（即将左端点右移一位），加上位置6（即将右端点右移一位），得到区间[2,6]的答案。

如果按这样写，一种很简单的构造数据就能把时间复杂度把算法2也送上天：先询问[1,2]，再询问[99999,100000],多重复几次就gg

但莫队算法是算法2的改进版

要进行合理的排序，使得每两个区间的距离最小

但如何进行合理的排序？

莫队提供了这样一个排序方案：将原序列以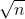为一块进行分块（分块的大小也珂以调整），排序第一关键字是询问的左端点所在块的编号，第二关键字是询问的右端点本身的位置，都是升序。然后我们用上面提到的“移动当前区间左右端点”的方法，按顺序求每个询问区间的答案，移动每一个询问区间左右端点可以求出下一个区间的答案。

莫队核心代码qaq：

sort(q+1,q+m+1,cmp); //讲询问按上述方法排序 
int l=1,r=0; //当前左端点和右端点初值（两只小手two-pointers） 
for(register int i=1;i<=m;++i) //对排序后的询问一个个转移 
{
    int ll=q[i].l,rr=q[i].r; //本次询问的区间 
    //转移，++--这些东西比较容易写错，需要注意 
    while(l<ll)
        del(l++);
    while(l>ll)
        add(--l);
    while(r<rr)
        add(++r);
    while(r>rr)
        del(r--);
    ans[q[i].id]=sth; //询问是排过序的，存到答案数组里需要返回原顺序 
}

这样就可以求出答案了！

——可是，这样做的复杂度是什么？

大约是

Luogu P3901 AC代码：

#pragma GCC optimize("O3")
#include <bits/stdc++.h>
#define N 100005
using namespace std;
inline int read()
{
    register int x=0,f=1;char ch=getchar();
    while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();}
    while(ch>=‘0‘&&ch<=‘9‘)x=(x<<3)+(x<<1)+ch-‘0‘,ch=getchar();
    return x*f;
}
int v[N],blocksize=0;
struct query{
    int l,r,id,bl;
}q[N];
int sum[N];
bool ans[N];
int cnt=0;
inline void add(register int x)
{
    if(++sum[v[x]]==1)
        ++cnt; 
}
inline void del(register int x)
{
    if(--sum[v[x]]==0)
        --cnt;
}
inline bool cmp(register query a,register query b)
{
    return a.bl==b.bl?a.r<b.r:a.bl<b.bl;
}
int main()
{
    memset(sum,0,sizeof(sum));
    int n=read(),m=read();
    blocksize=sqrt(n);
    for(register int i=1;i<=n;++i)
        v[i]=read();
    for(register int i=1;i<=m;++i)
    {
        int l=read(),r=read();
        q[i]=(query){l,r,i,(l-1)/blocksize+1};
    }
    sort(q+1,q+m+1,cmp);
    int l=1,r=0;
    for(register int i=1;i<=m;++i)
    {
        int ll=q[i].l,rr=q[i].r;
        while(l<ll)
            del(l++);
        while(l>ll)
            add(--l);
        while(r<rr)
            add(++r);
        while(r>rr)
            del(r--);
        ans[q[i].id]=(cnt==rr-ll+1)?1:0;
    }
    for(register int i=1;i<=m;++i)
        if(ans[i])
            puts("Yes");
        else
            puts("No");
    return 0;
 }