共线方程旋转矩阵转移向量等摄影测量知识综合

Posted 2021-01-21 zf-blog

参考链接： https://wenku.baidu.com/view/606da2a1240c844769eaee7e.html?qq-pf-to=pcqq.group

                   https://blog.csdn.net/fireflychh/article/details/82352710

先验知识：

（1）内方位元素：表示摄影中心与像片之间相关位置（姿态）的参数，共三个参数：

　　1)摄影中心s到像片的垂距；

　　2)像主点O在框标坐标系中的坐标（x₀ , y₀);

　　外方位元素：摄影中心在物方坐标系中的三维坐标和姿态（共6个参数）；

（2）四个坐标系：

　　1）框标坐标系：二维像平面坐标系；

　　2）像空间坐标系：Z轴垂直于二维像平面，X、Y轴平行于框标坐标系的X、Y轴；

　　3）像空间辅助坐标系（像辅坐标系）；

　　4）大地坐标系，也称物方坐标系：该坐标系与上面的像辅坐标系X、Y、Z轴均平行，只是原点位置不同，上者的原点在摄影中心（相机中心），该坐标系的原点在物体中心；

示意图如下：

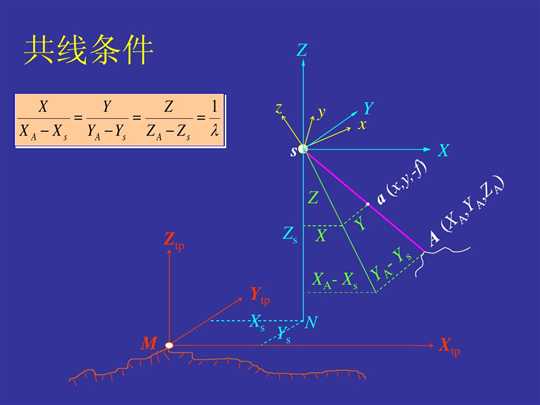
如上图：（X_tp , Y_tp , Z_tp）是物方坐标系，（X , Y , Z）是像辅坐标系，（x , y , z）是像空间坐标系，s是相机中心，a是物体A在像平面上的成像点；

1）（X_A , Y_A , Z_A）：A点物方坐标；

2）（X_S , Y_S , Z_S）：S点物方坐标；

3）（x , y , -f）：a点像空坐标；

4）（X , Y , Z）：a点像辅坐标；

另外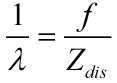，，其中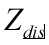为相机中心到物体中心的距离，f是相机的焦距；

现在我们先来证明共线方程：

在证明共线方程之前，我们需要县引入旋转矩阵（rotation matrix）这个概念，可以参考 https://blog.csdn.net/fireflychh/article/details/82352710

 详细解释如下：

然后我们也顺便引入translation vector的概念（即转移向量），我们令：

1）T_o-c：物体中心在像空坐标系中的坐标；

2）T_c-o：摄影中心（相机中心）在物方坐标系中的坐标；

然后来证明共线方程：

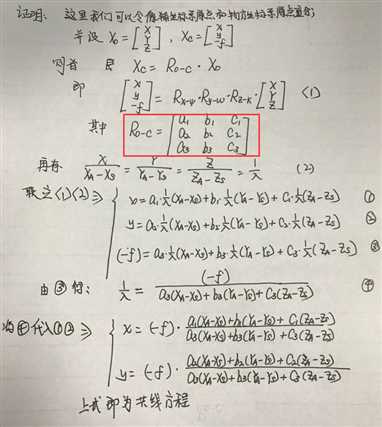
下面引入一个比较实用的公式，可以实现从物方坐标系到二维像平面坐标系的转换！如下：

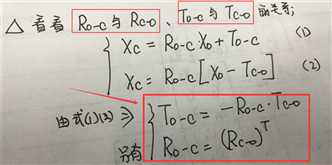
还有几点补充的：

（1）opencv中的两个函数：

　　1）cv::projectPoints(object_points2, rotation_matrix, translate_T, intrinsic_matrix, distortion_coeffs, pts_proj);  

　　2）solvePnP()

第一个函数是给定rotation_matrix和translate_T，可以计算出物方坐标投影到对应的像坐标，第二个函数是计算出rotation_matrix和translate_T，它们均为T_o-c , R_o-c；