LRU算法

Posted 2021-01-21 wyq178

前言：

【小王的困惑】

      首先考虑这样的一个业务场景,小王在A公司上班，有一天产品提出了一个需求：“咱们系统的用户啊，每天活跃的就那么多，有太多的僵尸用户，根本不登录，你能不能考虑做一个筛选机制把这些用户刨出去，并且给活跃的用户做一个排名，我们可以设计出一些奖励活动，提升咱们的用户粘性，咱们只需要关注那些活跃的用户就行了“”。小王连忙点头，说可以啊，然而心里犯起嘀咕来了：这简直，按照常规思路，给用户添加一个最近活跃时间长度和登录次数，然后按照这两个数据计算他们的活跃度，最后直接排序就行了。嘿嘿，简直完美!不过！用户表字段已经很多了，又要加两个字段，然后还得遍历所有的数据排序？这样查询效率是不是会受影响啊？并且公司的服务器上次就蹦过一次，差点没忙出命来才调好。有没有更优雅的一种方式呢？小王面朝天空45°，陷入了无限的思考中.....

本篇博客的目录

一：LRU是什么？

二：LRU的实现

三：测试

四：总结

一：LRU是什么？

1.1：LRU是什么？按照英文的直接原义就是Least Recently Used,最近最久未使用法，它是按照一个非常注明的计算机操作系统基础理论得来的：最近使用的页面数据会在未来一段时期内仍然被使用,已经很久没有使用的页面很有可能在未来较长的一段时间内仍然不会被使用。基于这个思想,会存在一种缓存淘汰机制，每次从内存中找到最久未使用的数据然后置换出来，从而存入新的数据！它的主要衡量指标是使用的时间，附加指标是使用的次数。在计算机中大量使用了这个机制，它的合理性在于优先筛选热点数据，所谓热点数据，就是最近最多使用的数据！因为，利用LRU我们可以解决很多实际开发中的问题，并且很符合业务场景。

1.2：小王的困惑

   当小王看到LRU的时候，瞬间感觉抓住了救命稻草，这个算法不是就完全契合产品的需求吗？只要把用户数据按照LRU去筛选，利用数据结构完成的事情，完全减少了自己存储、添加字段判断、排序的过程，这样对于提高服务器性能肯定有很大的帮助，岂不美哉！小王考虑好之后，就决定先写一个demo来实现LRU，那么在java中是如何实现LRU呢？考虑了许久，小王写下了这些代码。

二：LRU的实现

2.1：利用双向链表实现

双向链表有一个特点就是它的链表是双路的，我们定义好头节点和尾节点，然后利用先进后出（FIFO），最近被放入的数据会最早被获取。其中主要涉及到添加、访问、修改、删除操作。首先是添加，如果是新元素，直接放在链表头上面，其他的元素顺序往下移动；访问的话，在头节点的可以不用管，如果是在中间位置或者尾巴，就要将数据移动到头节点；修改操作也一样，修改原值之后，再将数据移动到头部；删除的话，直接删除，其他元素顺序移动；

2.2：java实现的代码

2.2.1：定义基本的链表操作节点

public class Node {
    //键
    Object key;
    //值
    Object value;
    //上一个节点
    Node pre;
    //下一个节点
    Node next;

    public Node(Object key, Object value) {
        this.key = key;
        this.value = value;
    }
}

　2.2.2：链表基本定义

我们定义一个LRU类，然后定义它的大小、容量、头节点、尾节点等部分，然后一个基本的构造方法

public class LRU<K, V> {
    private int currentSize;//当前的大小
    private int capcity;//总容量
    private HashMap<K, Node> caches;//所有的node节点
    private Node first;//头节点
    private Node last;//尾节点

    public LRU(int size) {
        currentSize = 0;
        this.capcity = size;
        caches = new HashMap<K, Node>(size);
    }

　　2.2.3：添加元素

添加元素的时候首先判断是不是新的元素，如果是新元素，判断当前的大小是不是大于总容量了，防止超过总链表大小，如果大于的话直接抛弃最后一个节点，然后再以传入的keyvalue值创建新的节点。对于已经存在的元素，直接覆盖旧值，再将该元素移动到头部，然后保存在map中

  /**
     * 添加元素
     * @param key
     * @param value
     */
    public void put(K key, V value) {
        Node node = caches.get(key);
        //如果新元素
        if (node == null) {
            //如果超过元素容纳量
            if (caches.size() >= capcity) {
                //移除最后一个节点
                caches.remove(last.key);
                removeLast();
            }
            //创建新节点
            node = new Node(key,value);
        }
        //已经存在的元素覆盖旧值
        node.value = value;
        //把元素移动到首部
        moveToHead(node);
        caches.put(key, node);
    }

　　2.2.4：访问元素

通过key值来访问元素，主要的做法就是先判断如果是不存在的，直接返回null。如果存在，把数据移动到首部头节点，然后再返回旧值。

    /**
     * 通过key获取元素
     * @param key
     * @return
     */
    public Object get(K key) {
        Node node = caches.get(key);
        if (node == null) {
            return null;
        }
        //把访问的节点移动到首部
        moveToHead(node);
        return node.value;
    }

如下所示，访问key=3这个节点的时候，需要把3移动到头部，这样能保证整个链表的头节点一定是特点数据(最近使用的数据！)

 

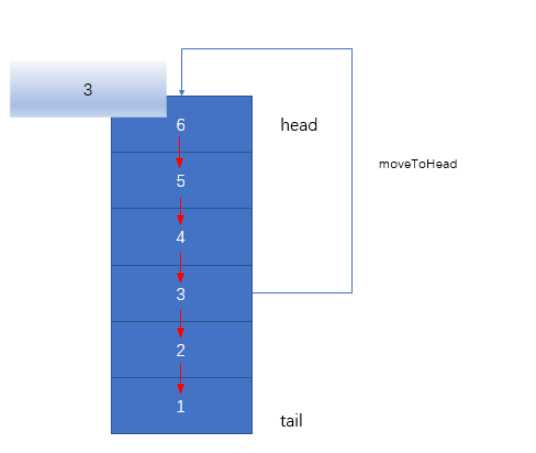
2.2.5：节点删除操作

在根据key删除节点的操作中，我们需要做的是把节点的前一个节点的指针指向当前节点下一个位置，再把当前节点的下一个的节点的上一个指向当前节点的前一个，这么说有点绕，我们来画图来看：

    /**
     * 根据key移除节点
     * @param key
     * @return
     */
    public Object remove(K key) {
        Node node = caches.get(key);
        if (node != null) {
            if (node.pre != null) {
                node.pre.next = node.next;
            }
            if (node.next != null) {
                node.next.pre = node.pre;
            }
            if (node == first) {
                first = node.next;
            }
            if (node == last) {
                last = node.pre;
            }
        }
        return caches.remove(key);
    }

　　假设现在要删除3这个元素，我们第一步要做的就是把3的pre节点4(这里说的都是key值)的下一个指针指向3的下一个节点2，再把3的下一个节点2的上一个指针指向3的上一个节点4，这样3就消失了，从4和2之间断开了，4和2再也不需要3来进行连接，从而实现删除的效果。

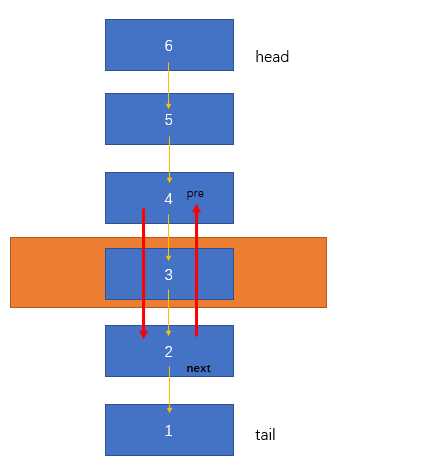
2.2.6：移动元素到头节点

首先把当前节点移除,类似于删除的效果(但是没有移除该元素)，然后再将首节点设为当前节点的下一个,再把当前节点设为头节点的前一个节点。当前几点设为首节点。再把首节点的前一个节点设为null，这样就是间接替换了头节点为当前节点。

    /**
     * 把当前节点移动到首部
     * @param node
     */
    private void moveToHead(Node node) {
        if (first == node) {
            return;
        }
        if (node.next != null) {
            node.next.pre = node.pre;
        } 
        if (node.pre != null) {
            node.pre.next = node.next;
        }
        if (node == last) {
            last = last.pre;
        }
        if (first == null || last == null) {
            first = last = node;
            return;
        }
        node.next = first;
        first.pre = node;
        first = node;
        first.pre = null;
    }

　　三：测试

代码写完了，我们来测试一下结果：

    public static void main(String[] args) {
        LRU<Integer, String> lru = new LRU<Integer, String>(5);
        lru.put(1, "a");
        lru.put(2, "b");
        lru.put(3, "c");
        lru.put(4,"d");
        lru.put(5,"e");
        System.out.println("原始链表为："+lru.toString());

        lru.get(4);
        System.out.println("获取key为4的元素之后的链表："+lru.toString());

        lru.put(6,"f");
        System.out.println("新添加一个key为6之后的链表："+lru.toString());

        lru.remove(3);
        System.out.println("移除key=3的之后的链表"+lru.toString());
    }

　　首先我们先新放入几个元素，然后再尝试访问第4个节点，再放入一个元素，再移除一个元素，看看会输出多少：

原始链表为:5:e 4:d 3:c 2:b 1:a 
获取key为4的元素之后的链表:4:d 5:e 3:c 2:b 1:a 
新添加一个key为6之后的链表:6:f 4:d 5:e 3:c 2:b 
移除key=3的之后的链表:6:f 4:d 5:e 2:b 

　　看结果发现和我们预期的一致，无论添加和获取元素之后整个链表都会将最近访问的元素移动到订点，这样保证了我们每次取到的最热点的数据，这就是LRU的最重要思想.

四：总结

   本篇博客主要讲述了LRU的算法实现，理解了LRU也能帮助我们理解LinkedList，因为linkedList本身就是双向链表。还有就是理解数据结构这种方式，以及LRU的移动节点的过程，如果能在实际的开发中利用它的特性使用到合适的业务场景中。

附加：java实现LRU的完整代码：

import java.util.HashMap;

public class LRU<K, V> {
    private int currentSize;//当前的大小
    private int capcity;//总容量
    private HashMap<K, Node> caches;//所有的node节点
    private Node first;//头节点
    private Node last;//尾节点

    public LRU(int size) {
        currentSize = 0;
        this.capcity = size;
        caches = new HashMap<K, Node>(size);
    }

    /**
     * 放入元素
     * @param key
     * @param value
     */
    public void put(K key, V value) {
        Node node = caches.get(key);
        //如果新元素
        if (node == null) {
            //如果超过元素容纳量
            if (caches.size() >= capcity) {
                //移除最后一个节点
                caches.remove(last.key);
                removeLast();
            }
            //创建新节点
            node = new Node(key,value);
        }
        //已经存在的元素覆盖旧值
        node.value = value;
        //把元素移动到首部
        moveToHead(node);
        caches.put(key, node);
    }

    /**
     * 通过key获取元素
     * @param key
     * @return
     */
    public Object get(K key) {
        Node node = caches.get(key);
        if (node == null) {
            return null;
        }
        //把访问的节点移动到首部
        moveToHead(node);
        return node.value;
    }

    /**
     * 根据key移除节点
     * @param key
     * @return
     */
    public Object remove(K key) {
        Node node = caches.get(key);
        if (node != null) {
            if (node.pre != null) {
                node.pre.next = node.next;
            }
            if (node.next != null) {
                node.next.pre = node.pre;
            }
            if (node == first) {
                first = node.next;
            }
            if (node == last) {
                last = node.pre;
            }
        }
        return caches.remove(key);
    }

    /**
     * 清除所有节点
     */
    public void clear() {
        first = null;
        last = null;
        caches.clear();
    }

    /**
     * 把当前节点移动到首部
     * @param node
     */
    private void moveToHead(Node node) {
        if (first == node) {
            return;
        }
        if (node.next != null) {
            node.next.pre = node.pre;
        }
        if (node.pre != null) {
            node.pre.next = node.next;
        }
        if (node == last) {
            last = last.pre;
        }
        if (first == null || last == null) {
            first = last = node;
            return;
        }
        node.next = first;
        first.pre = node;
        first = node;
        first.pre = null;
    }

    /**
     * 移除最后一个节点
     */
    private void removeLast() {
        if (last != null) {
            last = last.pre;
            if (last == null) {
                first = null;
            } else {
                last.next = null;
            }
        }
    }

    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder();
        Node node = first;
        while (node != null) {
            sb.append(String.format("%s:%s ", node.key, node.value));
            node = node.next;
        }
        return sb.toString();
    }
    

    public static void main(String[] args) {
        LRU<Integer, String> lru = new LRU<Integer, String>(5);
        lru.put(1, "a");
        lru.put(2, "b");
        lru.put(3, "c");
        lru.put(4,"d");
        lru.put(5,"e");
        System.out.println("原始链表为:"+lru.toString());

        lru.get(4);
        System.out.println("获取key为4的元素之后的链表:"+lru.toString());

        lru.put(6,"f");
        System.out.println("新添加一个key为6之后的链表:"+lru.toString());

        lru.remove(3);
        System.out.println("移除key=3的之后的链表:"+lru.toString());
    }
}