平衡树Treap

Posted 2021-01-20 cold-cold

Treap=BST+Heap,BST指的是二叉搜索树,而Heap指的是二叉堆,在此处我们使用的是小根堆.

　　Treap上的每一个结点都维护六个值,一个是它本身的权值data,一个是用于维护堆的性质的权值key(他是随机赋上的一个值),那么我们为什么要给每一个点赋一个随机的key值呢?可以由玄学证明key值随机赋值,可以使Treap的期望深度为logn，还有siz表示当前点为根的子树大小，cnt表示该该节点上有多少相同的节点，ls记录左儿子的编号，rs记录右儿子的编号

1. 左旋与右旋

　　

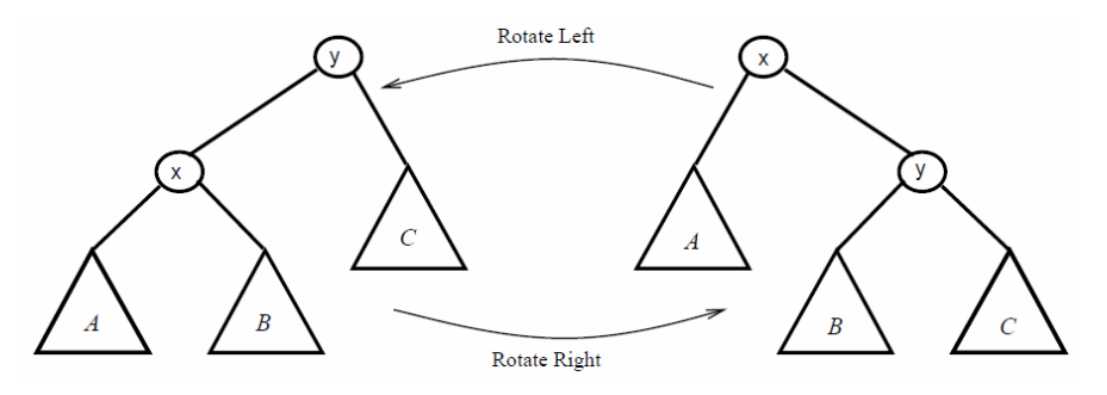
　　图中圆圈表示单个结点,而三角形表示一棵字树(字树可以为空),仔细观察这张图片,我们很容易发现旋转操作并不会影响到二叉搜索树所应该满足的性质，却可以使原本x,y的相对位置发生改变.所以当不满足堆的性质时,我们就可以使用左旋和右旋来维护堆的性质

左旋和右旋实现如下:

void zx(int &x)
{
    int y(rs[x]);
    rs[x]=ls[y];
    ls[y]=x;
    siz[y]=siz[x];
    siz[x]=siz[ls[x]]+siz[rs[x]]+cnt[x];
    x=y;
}

void yx(int &x)
{
    int y(ls[x]);
    ls[x]=rs[y];
    rs[y]=x;
    siz[y]=siz[x];
    siz[x]=siz[ls[x]]+siz[rs[x]]+cnt[x];
    x=y;
}

 2. 插入节点(insert)

插入节点的时候从根节点出发

(1) 如果当前节点为空，则将data赋为我们要插入的节点,siz和cnt初始化为1，再将其父亲连向他（这里我们要注意，二叉搜索树，是不记录父节点的，为了能使其父亲连向他，我们每次调用insert函数的时候我们传入其父亲指向其子节点的地址，而我们要使其父亲指向它，就是将该地址上的值改为新节点的编号）

(2) 如果要插入的节点比我们当前的节点小，就向该节点的左子树前进，同时，将该节点的siz加1(因为要插入的节点一定是插入到该节点的子树中去了)

(3) 如果要插入的节点比我们当前的节点大，就向该节点的右子树前进，同时，将该节点的siz加1(因为要插入的节点一定是插入到该节点的子树中去了)

(4) 如果要插入的节点等于我们当前的节点，就将该节点的cnt++，siz++

我们在插入节点后为该节点赋上一个随机的key值，如果该点的key值与其父亲相比不符合堆得性质，我们不能直接交换两个点，因为这样有可能会破坏二叉搜索树的性质，如果我们向右插入，就左旋该点，如果我们向左插入，就右旋该点。

是不是很容易呀，实现如下:

void insert(int &now,int v)
{
    if(!now)
    {
        data[now=++tot]=v;key[tot]=Rand();
        siz[tot]=cnt[tot]=1;
        return;
    }
    ++siz[now];
    if(data[now]==v) ++cnt[now];
    else if(data[now]<v)
    {
        insert(rs[now],v);
        if(key[now]>key[rs[now]]) zx(now);
    }
    else
    {
        insert(ls[now],v);
        if(key[now]>key[ls[now]]) yx(now);
    }
}

 3. 删除节点(del)

其实删除操作非常简单，我们从根节点出发

(1) 如果当前节点为空就返回

(2) 如果要插入的节点比我们当前的节点小，就向该节点的左子树前进，同时，将该节点的siz加1(因为要插入的节点一定是插入到该节点的子树中去了)

(3) 如果要插入的节点比我们当前的节点大，就向该节点的右子树前进，同时，将该节点的siz加1(因为要插入的节点一定是插入到该节点的子树中去了)

(4) 如果要插入的节点等于我们当前的节点

a) 若果当前节点cnt>1，就将cnt--即可

b) 如果该点只有一个儿子，就直接将该点的父亲连向该点的儿子，连接方法如上

c) 不然如果左儿子的key值比右儿子小，我们就右旋，再继续向右删除；如果左儿子的key值比右儿子大，我们就左旋，再继续向左删除

是不是很容易呀，实现如下:

void del(int &now,int v)
{
    if(!now) return;
    --siz[now];
    if(data[now]==v)
    {
        if(cnt[now]>1) --cnt[now];
        else if(!ls[now]||!rs[now]) now=ls[now]+rs[now];
        else if(key[ls[now]]<key[rs[now]])
        {
            yx(now);
            del(rs[now],v);
        }
        else
        {
            zx(now);
            del(ls[now],v);
        }
    }
    else if(data[now]<v) del(rs[now],v);
    else del(ls[now],v); 
}

 4. 快速伪随机(Rand)

stdlib.h 所自带的rand函数，不仅慢而且范围小，这就是我们需要自己手写伪随机了

　　确实容易呀，实现如下:

int seed=221520;
inline int Rand(){return seed=(seed*221ll)%MO;}

 

5. 查询某数排名(rank)

我们从根节点出发

　　(1) 如果当前节点为空就返回1

(2) 如果要插入的节点比我们当前的节点小，就向该节点的左子树继续查询

(3) 如果要插入的节点比我们当前的节点大，就向该节点的右子树继续查询，同时将查询得到的值+siz+cnt后返回

　　其实很容易写错，实现如下:

int rank(int &now,int v)
{
    if(!now) return 1;
    if(data[now]<v) return siz[ls[now]]+cnt[now]+rank(rs[now],v);
    else return rank(ls[now],v);
}

 

6. 查询第k大的数(kth)

我们从根节点出发

(1) 如果当前节点为空就返回-1(找不到)

(2) 如果要查的排名在该节点的范围内，就返回该节点

(3) 如果要插入的节点比我们当前的节点小，就向该节点的左子树继续查询

(4) 如果要插入的节点比我们当前的节点大，就向该节点的右子树继续查询排名为k-siz+-cnt的数

其实很容易写错，实现如下:

int kth(int &now,int v)
{
    if(!now) return -1;
    if(siz[ls[now]]<v&&v<=siz[ls[now]]+cnt[now]) return data[now];
    else if(siz[ls[now]]<v) return kth(rs[now],v-cnt[now]-siz[ls[now]]) ;
    else return kth(ls[now],v);
}

7. 求某数的前驱(前驱定义为小于该数，且最大的数)(pred)

我们从根节点出发

(1) 如果当前节点为空就返回-0x3f3f3f3f

(2) 如果要插入的节点比我们当前的节点小或等于我们当前的节点，就向该节点的左子树继续查询

(3) 如果要插入的节点比我们当前的节点大，就向该节点的右子树继续查询，并将查询得到的值与该点取最大值返回

　　其实很容易写错，实现如下:

int pred(int &now,int v)
{
    if(!now) return -0x3f3f3f3f;
    if(data[now]<v) return max(pred(rs[now],v),data[now]);
    else return pred(ls[now],v);
}

8. 求某数的后继(后继定义为大于该数，且最小的数)(succ)

我们从根节点出发

(1) 如果当前节点为空就返回0x3f3f3f3f

(2) 如果要插入的节点比我们当前的节点小，就向该节点的左子树继续查询，并将查询得到的值与该点取最小值返回

(3) 如果要插入的节点比我们当前的节点大或等于我们当前的节点，就向该节点的右子树继续查询

　　其实很容易写错，实现如下:

int succ(int &now,int v)
{
    if(!now) return 0x3f3f3f3f;
    if(data[now]<=v) return succ(rs[now],v);
    else return min(succ(ls[now],v),data[now]);
}

 是不是很容易呀，完整代码如下:

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <map>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <stack>
#include <vector>
#include <set>
using namespace std;
inline int read()
{
    int a=0,p=0;char ch=getchar();
    while((ch<‘0‘||ch>‘9‘)&&ch!=‘-‘) ch=getchar();
    if(ch==‘-‘) p=1,ch=getchar();
    while(ch>=‘0‘&&ch<=‘9‘) a=a*10+ch-48,ch=getchar();
    return p?-a:a;
}
const int N=100100,MO=1e9+7;
int data[N],tot(0),root(0),ls[N],rs[N],siz[N],cnt[N],key[N],seed=221520,n,op,x;
inline int Rand(){return seed=(seed*221ll)%MO;}
void zx(int &x)
{
    int y(rs[x]);
    rs[x]=ls[y];
    ls[y]=x;
    siz[y]=siz[x];
    siz[x]=siz[ls[x]]+siz[rs[x]]+cnt[x];
    x=y;
}
void yx(int &x)
{
    int y(ls[x]);
    ls[x]=rs[y];
    rs[y]=x;
    siz[y]=siz[x];
    siz[x]=siz[ls[x]]+siz[rs[x]]+cnt[x];
    x=y;
}
void insert(int &now,int v)
{
    if(!now)
    {
        data[now=++tot]=v;key[tot]=Rand();
        siz[tot]=cnt[tot]=1;
        return;
    }
    ++siz[now];
    if(data[now]==v) ++cnt[now];
    else if(data[now]<v)
    {
        insert(rs[now],v);
        if(key[now]>key[rs[now]]) zx(now);
    }
    else
    {
        insert(ls[now],v);
        if(key[now]>key[ls[now]]) yx(now);
    }
}
void del(int &now,int v)
{
    if(!now) return;
    --siz[now];
    if(data[now]==v)
    {
        if(cnt[now]>1) --cnt[now];
        else if(!ls[now]||!rs[now]) now=ls[now]+rs[now];
        else if(key[ls[now]]<key[rs[now]])
        {
            yx(now);
            del(rs[now],v);
        }
        else
        {
            zx(now);
            del(ls[now],v);
        }
    }
    else if(data[now]<v) del(rs[now],v);
    else del(ls[now],v); 
}
int rank(int &now,int v)
{
    if(!now) return 1;
    if(data[now]<v) return siz[ls[now]]+cnt[now]+rank(rs[now],v);
    else return rank(ls[now],v);
}
int kth(int &now,int v)
{
    if(!now) return -1;
    if(siz[ls[now]]<v&&v<=siz[ls[now]]+cnt[now]) return data[now];
    else if(siz[ls[now]]<v) return kth(rs[now],v-cnt[now]-siz[ls[now]]) ;
    else return kth(ls[now],v);
}
int pred(int &now,int v)
{
    if(!now) return -0x3f3f3f3f;
    if(data[now]<v) return max(pred(rs[now],v),data[now]);
    else return pred(ls[now],v);
}
int succ(int &now,int v)
{
    if(!now) return 0x3f3f3f3f;
    if(data[now]<=v) return succ(rs[now],v);
    else return min(succ(ls[now],v),data[now]);
}
int main()
{
    // freopen("data","r",stdin);
    // freopen("output","w",stdout);
    n=read();
    while(n--)
    {
        op=read(),x=read();
        if(op==1) insert(root,x);
        else if(op==2) del(root,x);
        else if(op==3) printf("%d
",rank(root,x));
        else if(op==4) printf("%d
",kth(root,x));
        else if(op==5) printf("%d
",pred(root,x));
        else printf("%d
",succ(root,x));
    }
    return 0;
}