20172305 2017-2018-2 《程序设计与数据结构》实验二报告

Posted 2021-01-18 sanjinge

20172305 2017-2018-2 《程序设计与数据结构》实验报告

课程：《程序设计与数据结构》
班级： 1723
姓名： 谭鑫
学号：20172305
实验教师：王志强
实验日期：2018年10月13日
必修/选修： 必修

实验内容

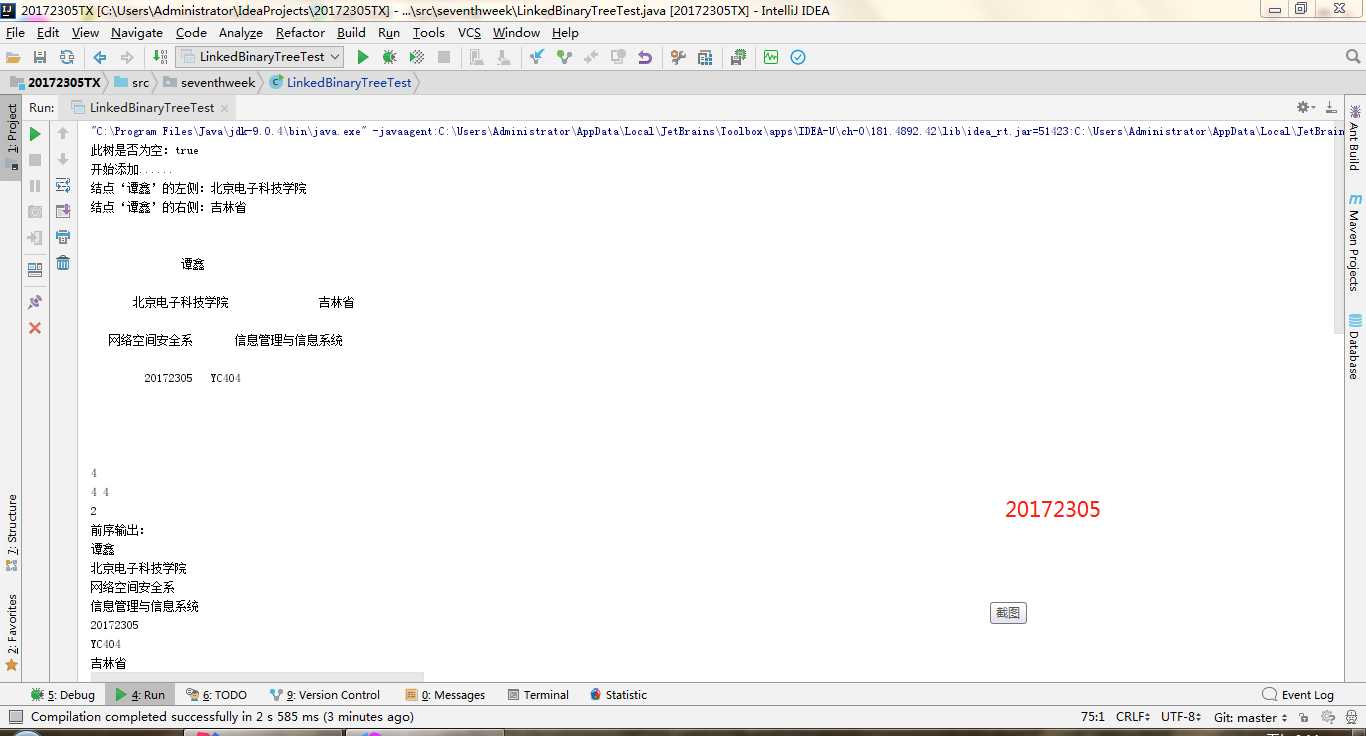
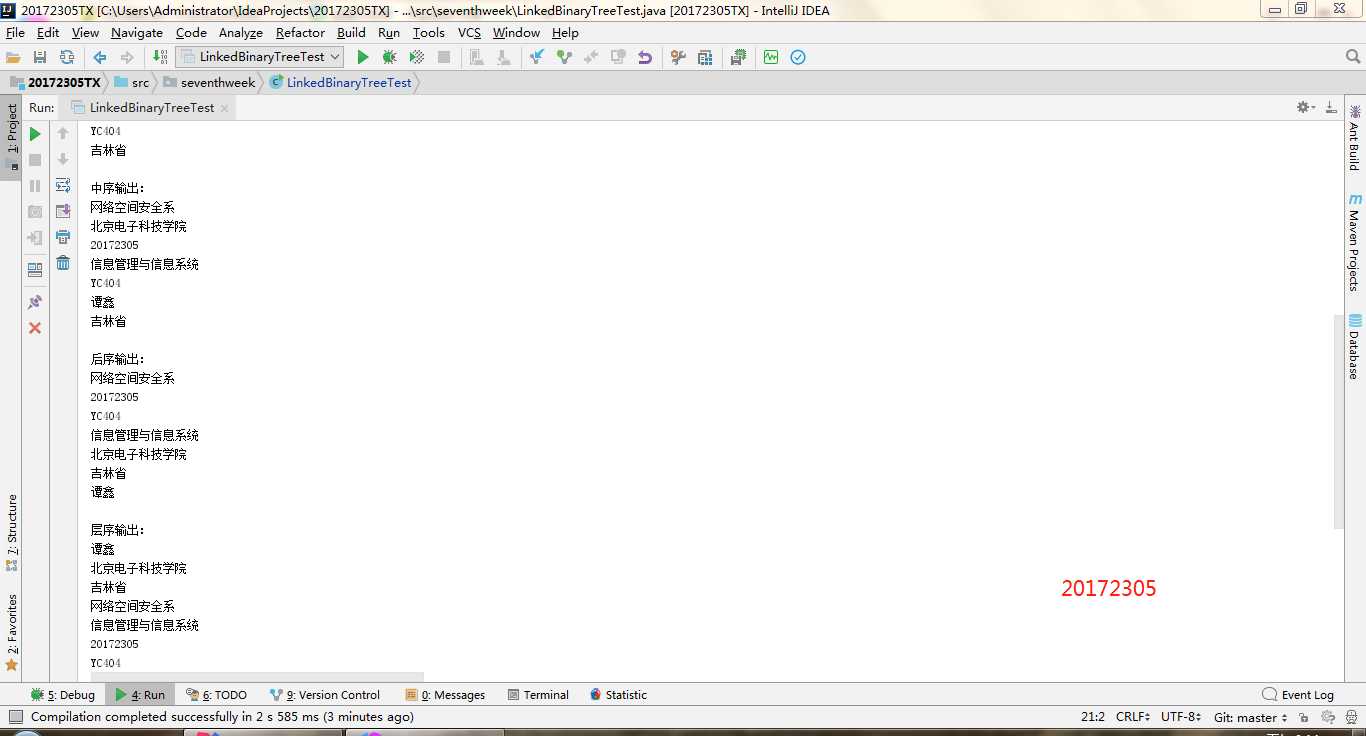
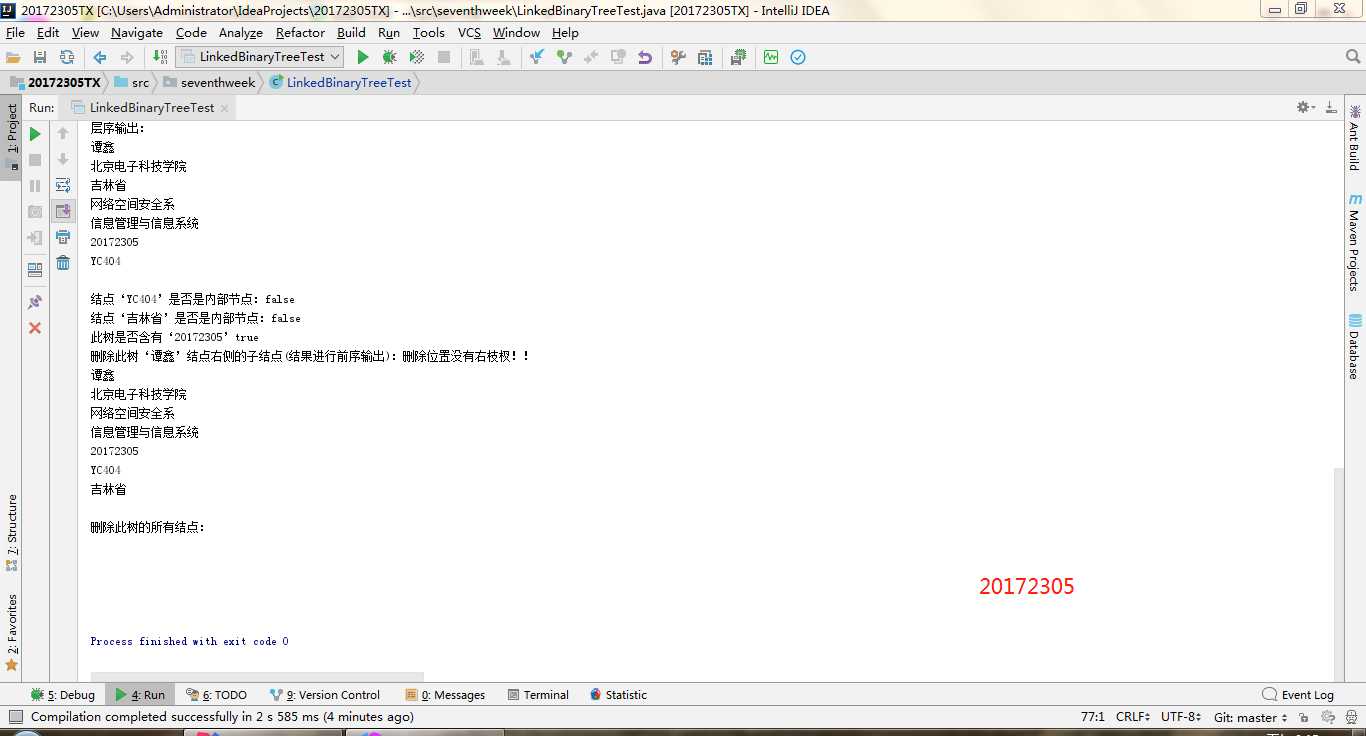
• 实验二-1-实现二叉树：
  • (1)参考教材p212,完成链树LinkedBinaryTree的实现（getRight,contains,toString,preorder,postorder）
  • (2)用JUnit或自己编写驱动类对自己实现的LinkedBinaryTree进行测试
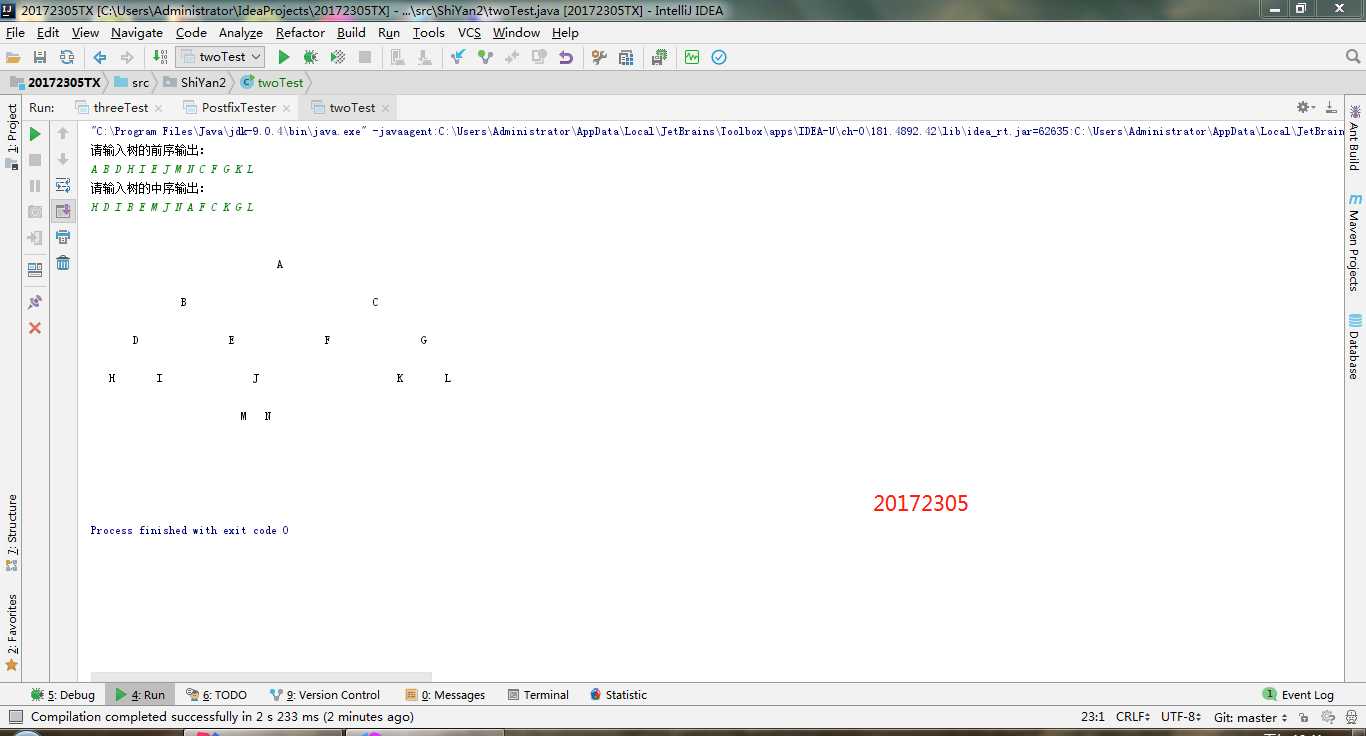
• 实验二-2-中序先序序列构造二叉树：
  • (1)基于LinkedBinaryTree，实现基于（中序，先序）序列构造唯一一棵二?树的功能，比如给出中序HDIBEMJNAFCKGL和后序ABDHIEJMNCFGKL,构造出树
  • (2)用JUnit或自己编写驱动类对自己实现的功能进行测试
• 实验二-3-决策树：
  • (1)设计并实现一棵决策树
  • (2)用JUnit或自己编写驱动类对自己实现的功能进行测试
• 实验二-4-表达式树：
  • (1)输入中缀表达式，使用树将中缀表达式转换为后缀表达式，并输出后缀表达式和计算结果
  • (2)用JUnit或自己编写驱动类对自己实现的功能进行测试
• 实验二-5-二叉查找树：
  • (1)完成PP11.3
  • (2)用JUnit或自己编写驱动类对自己实现的功能进行测试
• 实验二-6-红黑树分析：
  • (1)参考文件对Java中的红黑树（TreeMap，HashMap）进行源码分析，并在实验报告中体现分析结果。（C:Program FilesJavajdk-11.0.1libsrcjava.basejavautil）

实验过程及结果

• 实验二-1-实现二叉树：就是对二叉树的测试，二叉树不像二叉查找树一样可以进行添加删除。所以，在构造一个二叉树的时候需要不断的new一下，把每一个结点进行拼接才能构造一棵树。getRight,contains,toString,preorder,postorder。

  • getRight和getLeft,是返回某结点的左侧和右侧的操作
  • contains,是判定指定目标是否在该树中的操作
  • toString,是将树进行输出
  • preorder,是对树进行前序遍历
  • postorder,是对树进行后序遍历
  • 具体分析在第六周博客

• 实现的操作相对简单，只是遍历的时候发现迭代器运用起来感觉很麻烦，所以就根据遍历思想创建了四个简单点的遍历方法。
  • LinkedBinaryTree

  • LinkedBinaryTreeTest

    
    
    

• 实验二-2-中序先序序列构造二叉树:根据中序和先序的内容来判断树内元素的具体位置，通过先序来判断根结点，再在中序来判断根结点的左子树和右子树；在将两个部分继续在先序中查询根结点，在中序中判断结点的左右子树，就会判断出树中各个结点的位置。
  • PreIntree

  • Test

    

• 实验二-3-决策树：实现一棵决策树，这个实验就是仿照书上第十章的背部疼痛诊断器来书写的。我再此基础上并没有进行大的修改，只是仿照内容修改了读取的文件内容。我所设计的决策树内容如图：

  

  • DesicionTree

  • Test

    

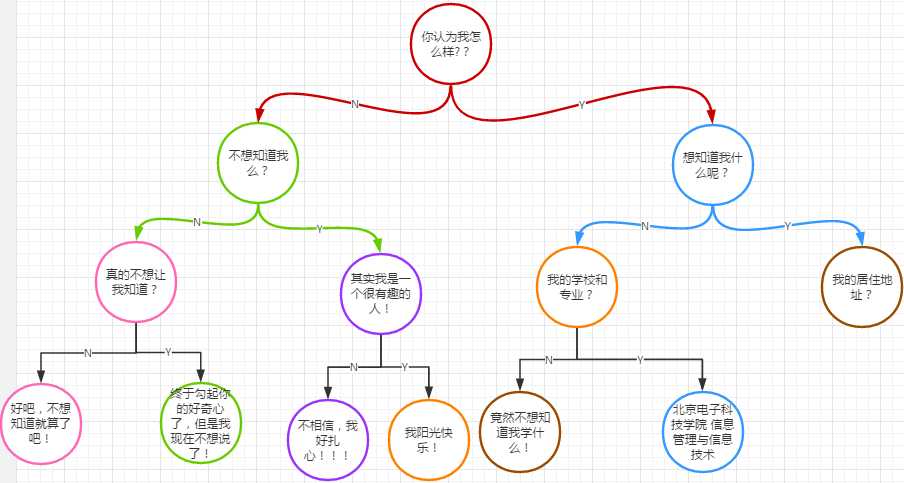
• 实验二-4-表达式树：通过输入的中缀表达式利用树来实现中缀转后缀，并由二叉树转换成后缀表达式并输出。
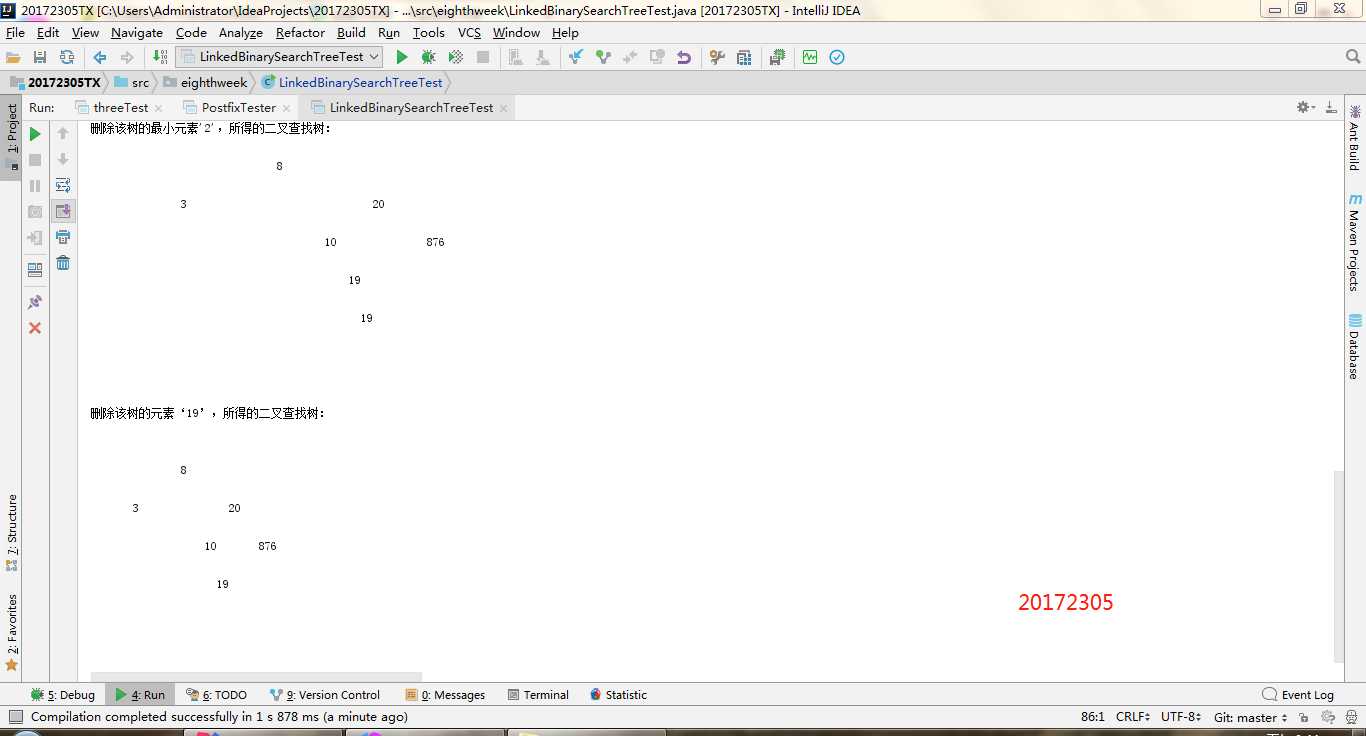
  在实现后缀的过程中，我们可以调用之前的书上代码来实现后缀表达式的转换成数字。
  • PostfixEvaluator
  • InfixSuffixTree

  • Test

    

• 实验二-5-二叉查找树：就是对二叉查找树的测试，二叉查找树会优于二叉树可以进行添加删除。所以，在构造一个二叉查找树的时候，把每一个结点内的内容加进去就可以。
  • LinkedBinarySearchTree

  • LinkedBinarySearchTreeTest

    

• 实验二-6-红黑树：红黑树的问题是最麻烦的，根据每一个树的结点内容实现红黑的添加，但是红黑的添加会出现碰撞，这就需要我们的具体分析过程，而TreeMap和TreeSet方法都是依靠红黑树来实现的。

  红黑树的性质：

  • (1)每个结点或者是黑色，或者是红色
  • (2)根结点是黑色
  • (3)每个叶结点是黑色(是指为空的叶结点)
  • (4)如果一个结点是红色的，则它的子节点必须是黑色的
  • (5)从一个结点到该结点的子孙结点的所有路径上包含相同数目的黑结点
    

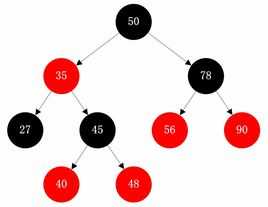
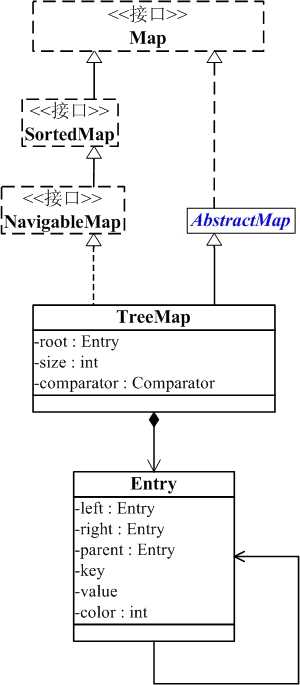
  • TreeMap和TreeSet是API的两个重要成员，其中 TreeMap是Map接口的常用实现类，而TreeSet是Set接口的常用实现类。虽然TreeMap和TreeSet实现的接口规范不同，TreeMap实现的接口是Map，TreeSet实现的接口是Set，但TreeSet底层是通过TreeMap来实现的，因此二者的实现方式完全一样。而TreeMap底层的实现就是用的红黑树数据结构来实现的。

  • TreeMap是一个有序的key-value集合，它是通过红黑树实现的。
  • TreeMap继承于AbstractMap，所以它是一个Map，即一个key-value集合。
  • TreeMap实现了NavigableMap接口，意味着它支持一系列的导航方法。比如返回有序的key集合。
  • TreeMap实现了Cloneable接口，意味着它能被克隆。
  • TreeMap实现了java.io.Serializable接口，意味着它支持序列化。
    
  • TreeMap的简单测试：
    

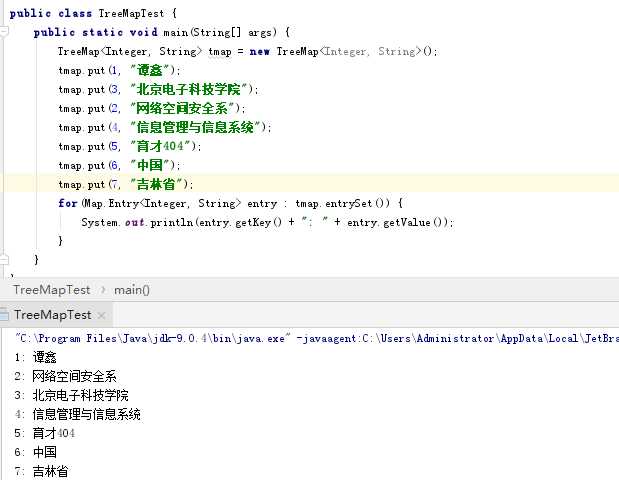
• 关于Set接口：Set接口代表不允许重复元的Collection。由接口SortedSet给出的一种特殊类型的Set保证其中的各项处于有序状态。由于Set所要求的一些独特的操作是一些插入、删除以及有效的执行查找能力。对于Set,add方法如果执行成功就返回true,否则返回false，因为被添加项已经存在。保持各项有序状态的Set的实现是TreeSet。

• 关于Map接口：Map接口代表由关键字以及它们的值组成的一些项的集合。关键字必须是唯一的，但是若干关键字的可以映射到一些相同的值。因此，值不是唯一的。在SortedMap接口中，映射中的关键字保持逻辑上有序状态。SortedMap接口的一种实现是TreeMap。

  TreeMap和TreeSet的相同点：

  • TreeMap和TreeSet都是有序的集合，也就是说他们存储的值都是拍好序的。
  • TreeMap和TreeSet都是非同步集合，因此他们不能在多线程之间共享，不过可以使用方法Collections.synchroinzedMap()来实现同步
  • 运行速度都要比Hash集合慢，他们内部对元素的操作时间复杂度为O(logN)，而HashMap/HashSet则为O(1)。

  TreeMap和TreeSet的不同点：

  • 最主要的区别就是TreeSet和TreeMap非别实现Set和Map接口
  • TreeSet只存储一个对象，而TreeMap存储两个对象Key和Value（仅仅key对象有序）
  • TreeSet中不能有重复对象，而TreeMap中可以存在

// 默认构造函数。使用该构造函数，TreeMap中的元素按照自然排序进行排列。
    TreeMap()

// 创建的TreeMap包含Map
    TreeMap(Map<? extends K, ? extends V> copyFrom)

// 指定Tree的比较器
    TreeMap(Comparator<? super K> comparator)

// 创建的TreeSet包含copyFrom
    TreeMap(SortedMap<K, ? extends V> copyFrom)

//默认构造方法，根据其元素的自然顺序进行排序
    public TreeSet()
    
//构造一个包含指定 collection 元素的新TreeSet，它按照其元素的自然顺序进行排序。
    public TreeSet(Comparator<? super E> comparator) 
    
//构造一个新的空TreeSet，它根据指定比较器进行排序。
    public TreeSet(Collection<? extends E> c)
    
//构造一个与指定有序 set具有相同映射关系和相同排序的新 TreeSet。
    public TreeSet(SortedSet<E> s)

• TreeMap的Empty方法，firstEntry()和getFirstEntry()都是用于获取第一个节点。但是，firstEntry() 是对外接口；getFirstEntry()是内部接口。而且，firstEntry()是通过getFirstEntry()来实现的。两个方法并会显得很麻烦，因为通过firstEntry()方法和可以避免修改返回的Entry，这样保证了完整性，而且产生了两个方法，一个可以是避免修改的方法，一个可以是修改的方法。通过查阅资料可以总结出对firstEntry()返回的Entry对象只能进行getKey()、getValue()等读取操作；而对getFirstEntry()返回的对象除了可以进行读取操作之后，还可以通过setValue()修改值。

public Map.Entry<K,V> firstEntry() {
    return exportEntry(getFirstEntry());
}

final Entry<K,V> getFirstEntry() {
    Entry<K,V> p = root;
    if (p != null)
        while (p.left != null)
            p = p.left;
    return p;
} 

• TreeMap的Key方法，返回大于/等于key的最小的键值对所对应的KEY，没有的话返回null。

public K ceilingKey(K key) {
    return keyOrNull(getCeilingEntry(key));
}

• TreeMap的values方法，values方法是通过new Values()来实现返回TreeMap中值的集合，而Values()正好是集合类Value的构造函数，这样返回的是一个集合了。

public Collection<V> values() {
    Collection<V> vs = values;
    return (vs != null) ? vs : (values = new Values());
}

• TreeMap的entrySet方法，entrySet方法是返回TreeMap的所有键值对组成的集合，而且它单位是单个键值对。

public Set<Map.Entry<K,V>> entrySet() {
    EntrySet es = entrySet;
    return (es != null) ? es : (entrySet = new EntrySet());
}

• TreeMap还有两个遍历方法，顺序遍历和逆序遍历，顺序遍历，就是从第一个元素开始，逐个向后遍历；而倒序遍历则恰恰相反，它是从最后一个元素开始，逐个往前遍历。
• TreeMap遍历键值对的方法，先根据entrySet()获取TreeMap的“键值对”的Set集合，再通过迭代器遍历得到的集合。

Integer integ = null;
Iterator iter = map.entrySet().iterator();
while(iter.hasNext()) {
    Map.Entry entry = (Map.Entry)iter.next();
    key = (String)entry.getKey();
    integ = (Integer)entry.getValue();
}

• TreeMap遍历键的方法，先keySet()获取TreeMap的键的Set集合，再通过迭代器遍历得到的集合。

String key = null;
Integer integer = null;
Iterator iter = map.keySet().iterator();
while (iter.hasNext()) {
    key = (String)iter.next();
    integer = (Integer)map.get(key);
}

实验过程中遇到的问题和解决过程

• 问题1：如何利用先序和后序转换成整棵树？

• 问题1的解决方案：根据先序来查找根结点的位置，再在中序查找到根结点，通过根结点的位置分出左子树和右子树两个部分。将每一部分重新看成一个树，并在先序中查找到这部分的根结点(此为根结点的右子结点)，再进行右侧部分，不断地递归下去就会实现，当这个中序中的位置和后序中的元素一致，就会结束。

  

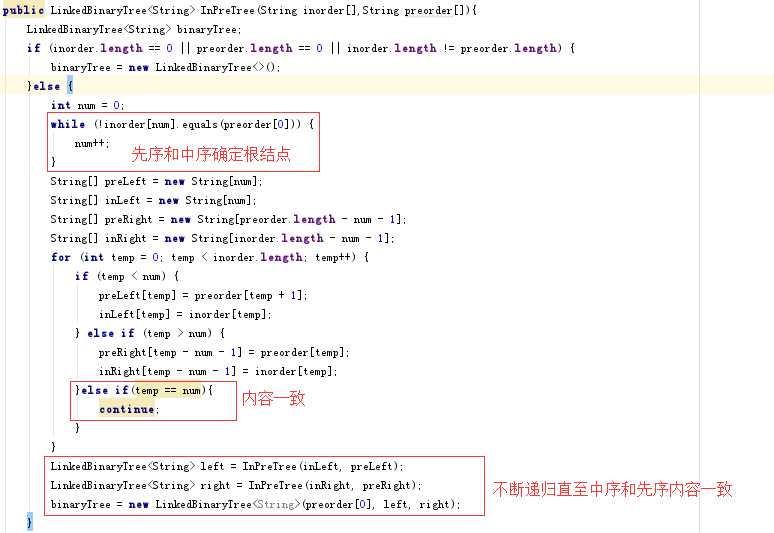
• 问题2：如何利用树实现中缀转后缀得出结果？

• 问题2的解决方案：在上学期实现的四则运算的思路来看，整个运算式需要先不断截取成一个字符，把运算符方法放到一个无序列表，将数放到一个定义为链表式树类的无序列表。针对运算的逻辑顺序，括号内的优先级最高，乘除的运算其次，最后是加减的运算。所以，在断开存放的时候先判断括号，如果遇到括号，那么直至查找到另一半括号，中间的内容都为括号内的，将这一部分整体作为一个新的运算式通过递归不断打开，使得括号内的内容拆成一棵树，将这部分的树存放到无序列表中。通过判断截取存放的过程将运算符为加减的存放到无序列表，遇到乘除的时候将存放树的无序列表取出最后一个(为乘除前一位内容可能是括号展成的树或是数字)，判断后面是否为括号，如果为括号就取到另一半括号为止，这样同样是用到递归来实现拆分成树，将取到的乘除作为根结点，前面的内容作为左子树，后面的内容作为右子树；如果是不为括号，那么就是个数，就将数作为树，这不过是一个只有根结点没有左右结点的树，加上之前的乘除号重新做一个树，存放到无序列表中，最后该无序列表会只存放一个树，只需输出一下就好。

    public BinaryTreeNode change(String strings){
     //把“=”进行抠出
     StringTokenizer tokenizer = new StringTokenizer(strings,"=");
     String string = tokenizer.nextToken();
     //开始转换
     StringTokenizer stringTokenizer = new StringTokenizer(string," ");
     ArrayUnorderedList<String> arrayUnorderedList1 = new ArrayUnorderedList<String>();
     ArrayUnorderedList<LinkedBinaryTree> arrayUnorderedList2 = new ArrayUnorderedList<LinkedBinaryTree>();
     while (stringTokenizer.hasMoreTokens()){
         strings = stringTokenizer.nextToken();
         //判断式子中是否有括号
         boolean judge1 = true;
         if(strings.equals("(")){
             String string1 = "";
             while (judge1){
                 strings = stringTokenizer.nextToken();
                 //开始查询括号的另一个，如果查到的话就会跳出该循环
                 if (!strings.equals(")"))
                     string1 += strings + " ";
                 else
                     break;
             }  
             LinkedBinaryTree linkedBinaryTree = new LinkedBinaryTree();
             linkedBinaryTree.root = (change(string1));
             arrayUnorderedList2.addToRear(linkedBinaryTree);
             continue;
         } 
         //判断运算符是否是加减的运算
         if((strings.equals("+")|| strings.equals("-"))){
             arrayUnorderedList1.addToRear(strings);
         }else
             ///判断运算符是否是乘除的运算
             if((strings.equals("*")|| strings.equals("/"))){
             LinkedBinaryTree left = arrayUnorderedList2.removeLast();
             String strings2 = strings;
             strings = stringTokenizer.nextToken();
             if(!strings.equals("(")) {
                 LinkedBinaryTree right = new LinkedBinaryTree(strings);
                 LinkedBinaryTree node = new LinkedBinaryTree(strings2, left, right);
                 arrayUnorderedList2.addToRear(node);
             }else {
                 String string3 = "";
                 boolean judge2 = true;
                 while (judge2){
                     strings = stringTokenizer.nextToken();
                     if (!strings.equals(")"))
                         string3 += strings + " ";
                     else break;
                 } 
                 LinkedBinaryTree linkedBinaryTree = new LinkedBinaryTree();
                 linkedBinaryTree.root = (change(string3));
                 LinkedBinaryTree node = new LinkedBinaryTree(strings2,left,linkedBinaryTree);
                 arrayUnorderedList2.addToRear(node);
             }
         }else
             arrayUnorderedList2.addToRear(new LinkedBinaryTree(strings));
     }
  
     while(arrayUnorderedList1.size()>0){
         LinkedBinaryTree left = arrayUnorderedList2.removeFirst();
         LinkedBinaryTree right = arrayUnorderedList2.removeFirst();
         String oper = arrayUnorderedList1.removeFirst();
         LinkedBinaryTree node = new LinkedBinaryTree(oper,left,right);
         arrayUnorderedList2.addToFront(node);
     }
     root = (arrayUnorderedList2.removeFirst()).getRootNode();
     return root;
    }

其他

实验二的六个实验看似很多实际上就第二个、第四个和第六个实验需要认真修改的。这三个实验的不同提交时间可以减少不小麻烦。但是实验四的设计思路还是很费劲，构思出但是不会用代码实现，还有是否要加括号的问题，如果添加那么就需要在优先级上进行改写，好在最后写出来了。感觉这学期的实验更多的是偏向于逻辑算法的，就像本次实验这样，需要更多的思路要考虑。

参考资料

• TreeMap
• TreeMap与TreeSet