一.进位计数制
1.进制表示:

表示b进制下的n+1位数。
2.进制转换:
进制向十进制转换:
乘以基数并展开:

十进制向b进制转换:
整数部分除以基数并倒取余数。
小数部分乘以基数,并顺取整数部分

3.例题:
a.天平1:
一个天平,有N个重量未知的砝码,砝码重量可由你自由确定。
砝码可任意放在天平的左右两边,但要求称出从1到M之间所有的重量,
现给出\\(N\\)的值,请问M最大值为多少。
答案:\\([0,3^N]\\)。具体见下面解析。
b.天平2:
一个天平,砝码分别为1g、3g、9g、27g、…、6561g…,
每个砝码只有一个,要称重的物品放在天平的左侧,而砝码允许放在天平的左右两侧。
已知一个物品的质量N (N≤108 ),问如何称重?
_____________________________________________________________________
解析:
就是将\\(N\\)转换成三进制后,
将三进制中的0、1、2三个状态转换成 0、1 、-1
具体的说,就是0和1不变,2变成-1后,其高一位加1。
例如:
\\(N\\)转化为三进制后为{1,2,0,1} , 那么对应的状态为:{1,-1,-1,0,1}。
即三进制中的2是没法直接称量的,因为每个重量的砝码只有一个,所以只能通过相减来处理。
c.天平3:
一个天平,砝码分别为1g、3g、9g、27g、…、6561g…,每个砝码只有一个,
要称重的物品放在天平的左侧,而砝码只允许放在天平的右侧。
将由这个系统可以称出来的重量按从小到大的顺序进行排列,
得到下列序列:1,3,4,9,10,...。问其中的第K个重量是多少?
_____________________________________________________________________
解析:仔细观察就可以发现,将K转化为二进制后,为1的即放置对应质量的三进制重量砝码即可。
二.素数和合数
1.素数判定:
枚举\\(\\sqrt{N}\\)内的质因子即可。 时间复杂度\\(O(\\sqrt{N})\\)。
2.欧拉筛法(线性筛素数)
原理:?每个合数必有一个最小素因子,用这个因子筛掉合数。
实现代码(筛出\\([0,N]\\)的素数):
void Prime(int N){
memset(isPrime,true,sizeof(isPrime));
isPrime[0 ] = false ; isPrime[1] = false ;
for (int i = 2 ; i <= N ; i++){
if ( isPrime[i] )prime[++ total] = i ; //把素数记录下来
//遍历已知素数表中比i的最小素因数小的素数,并筛去合数
for(int j = 1 ; j <= total && i * prime[j] <= N ; j++){
isPrime[ i * prime[j] ] = false ;
if (!( i % prime[j])) break; //找到i的最小素因数
}
}
}
三.唯一分解定理
对任一整数\\(a>1\\),有\\(a= p_1^{a_1}p_2^{a_2}…p_n^{a_n}\\)
几个比较重要的结论(证明都很显然)。
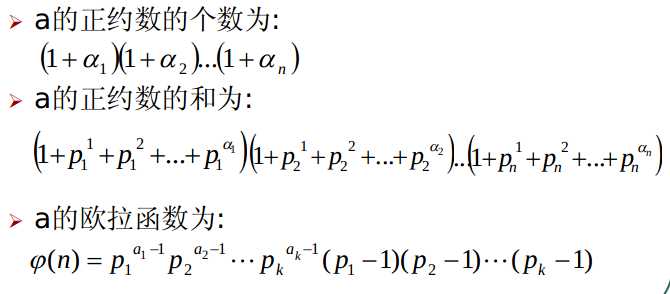
四.欧拉函数
1.定义:
欧拉函数: \\([1,n]\\)中和\\(n\\)互素的元素个数 \\(φ(n)\\)
\\[φ(n) = \\Sigma_{i=1}^{n} [gcd(i,n) ==1]\\]
2.性质:
<1> 如果\\(n\\)为某一素数\\(p\\),则\\(φ(p)=p-1\\)
<2> 如果\\(n\\)为某一素数\\(p\\)的幂次\\(p^a\\),\\(φ(p^a)=(p-1)×p^{a-1}\\)
证明:\\(φ(p^{a}) = φ(p^{a-1})*p = (p^a-1)*(1-\\frac{1}{p})*p = (p-1)×p^{a-1}\\)<3> 欧拉函数是积性函数,即当\\(gcd(m,n)=1\\)时 \\(f(mn)=f(m)*f(n)\\)
<4> 欧拉函数计算公式:
设\\(p_1^{a_1}×p_2^{a_2}×…×p_k^{a_k}\\)为正整数n的素数乘积式,则
\\[φ(n) =n×(1-\\frac{1}{p_1}) ×(1-\\frac{1}{p_2})×…×(1-\\frac{1}{p_k})\\]
3.欧拉函数线性筛
void eular(int n){
for(int i=2;i<=n;i++){
if (!IsPrime[i])prime[++cnt]=i,phi[i]=i-1;
for(int j=1;j<=cnt;j++){
if(prime[j]*i>n)break;
Isprime[prime[j]*i]=1;
if(i%prime[j]==0)
{phi[i*prime[j]]=phi[i]*prime[j]; break;} //p是x的约数
else
phi[i*prime[j]]=phi[i]*(prime[j]-1); //p不是x的约数
}
}return;
} 理解:
设P是素数,
若p是x的约数,则\\(φ(x*p)=φ(x)*p\\)
//没有加项。
若p不是x的约数,则\\(φ(x*p)=φ(x)*φ(p)=φ(x)*(p-1).\\)
//加了一项,即\\(φ(x*p) = φ(x)*p*(1-\\frac{1}{p}) = φ(x)*(p-1);\\)
例题:
例一:Poj 2773Happy 2006
给出一个数字\\(M\\) (\\(1 \\leq M \\leq 10^6\\)), 数字\\(K\\) (\\(1 \\leq K \\leq 10^8\\)).求与M互质的第K个数字
_____________________________________________________________________
解法1:
注意到若(a,m) = 1,那么(a+m*k,m)=1
所以实际上与m互质的数分布是一个分块区间。
以[1,m]为一个周期循环,此法常数要卡一卡。
______________________________________________________________________
解法2:
先二分这个值n,
然后检查小于等于n且与m互质的数的个数。
先处理出m的因数,然后用\\(φ(x)\\)容斥即可。
例二:[SDOI2012]Longge的问题
求:\\(∑gcd(i, N)\\) , \\((1\\leq i \\leq N)\\) , 其中$0<N\\leq 2^{32}
$ 。
解析:见博客:http://www.cnblogs.com/GuessYCB/p/8192826.html