阿白数模笔记之模拟退火算法(simulated annealing,SA)
Posted 阿白啥也不会
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了阿白数模笔记之模拟退火算法(simulated annealing,SA)相关的知识,希望对你有一定的参考价值。
目录
模拟退火简介(brief introduction of SA)
②寻找全局最优解(Find the global optimal solution)
①马尔科夫链长(length of Markov chain)
③衰减系数(Attenuation coefficient)
前言(preface)
在使用梯度下降法或牛顿法寻找最优解时,对下图的 BCD 四点,都可能"误入歧途"陷入局部最优解,这是因为在迭代的过程中自动舍弃了旧解 ,而SA 通过一定概率保留旧解(Metropolos准则),从而可能跳出局部最优解,找到全局最优解。
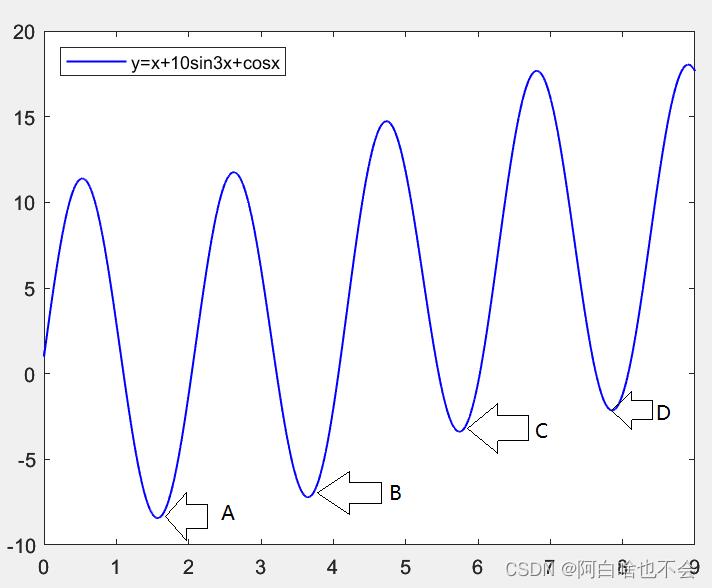
x=linspace(0,9,10000);
f=@(x) x+10*sin(3*x)+cos(x);
y=f(x);
plot(x,y,'b-','linewidth',1);
legend('y=x+10sin3x+cosx','location','northwest')模拟退火简介(brief introduction of SA)
模拟退火算法来源于固体退火原理,将固体加温至充分高,再让其徐徐冷却,加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。根据Metropolis准则,粒子在温度T时趋于平衡的概率为e(-ΔE/(kT)),其中E为温度T时的内能,ΔE为其改变量,k为Boltzmann常数。用固体退火模拟组合优化问题,将内能E模拟为目标函数值f,温度T演化成控制参数t,即得到解组合优化问题的模拟退火算法:由初始解i和控制参数初值t开始,对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代,并逐步衰减t值,算法终止时的当前解即为所得近似最优解,这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制,包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。——百度百科
实例分析(Case analysis)
①初始参数(Initial parameters)
t0=20000; %初始温度(initial temperature)
tend=1e-7; %结束温度 (final temperature)
l=400; %马尔科夫链长(length of Markov chain)
a=0.98; %衰减系数 (Attenuation coefficient)
s1=3; %初始解(Initial solution)②寻找全局最优解(Find the global optimal solution)
Metropolos准则:从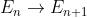 的接受概率为
的接受概率为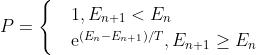
tset=1;p=1; %记录迭代次数
y0=f(s1); %记录解
while t0>tend %退火过程实施
k=1;
while k<=l %内层循环
if (0<s1)&&(s1<9) %定义域内
snew=s1+0.01*(2*rand(1)-1);
elseif s1<=0
snew=s1+0.01*rand(1);
else
snew=s1-0.01*rand(1);
end
if f(snew)<f(s1)
s1=snew;
else
r=rand(1);
if r<exp((f(s1)-f(snew))/t0) %Metropolos准则
s1=snew;
end
end
k=k+1;
end
t0=t0*a;
tset=[tset,p];p=p+1;
y0=[y0,f(s1)];
end③迭代过程图示
需要注意的是,对一组参数应执行多次取最优;同时,还应当调整初始解等参数横向对比
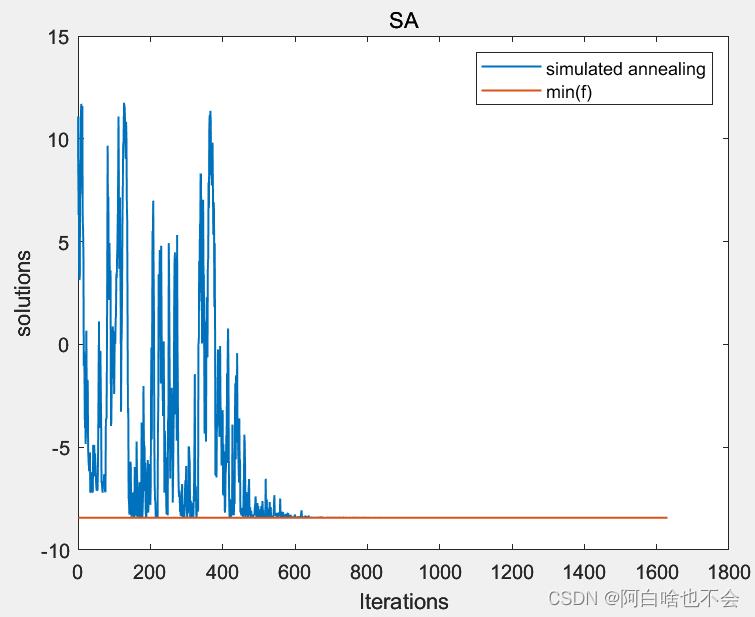
figure,plot(tset,y0,[tset(1),tset(end)],[min(y),min(y)],'linewidth',1);
legend('simulated annealing','min(f)');
title('SA')
xlabel('Iterations');ylabel('solutions')
模拟退火算法的不足(shortcoming)
①马尔科夫链长(length of Markov chain)
理论上,马尔科夫链越长,搜索的越充分,但相应的也会耗费计算时间。下图是s1=3(初始解)时候,l=400,700,1000的迭代次数和解,l=400时同样陷入了局部最优解

②初始解(initial solution)
在其他初始参数一定的情况下,初始解的选择有可能导致陷入局部最优解。下面是l=500时,s1=2,5,8的情况
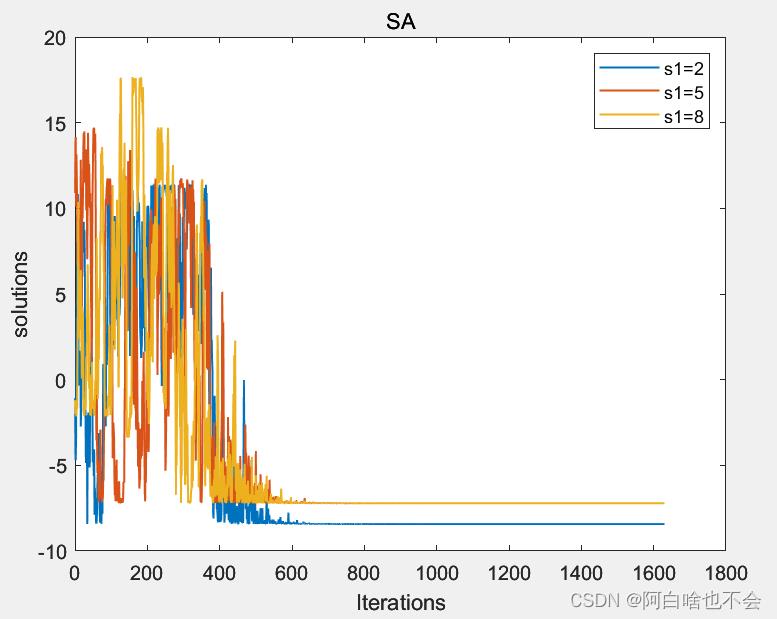
③衰减系数(Attenuation coefficient)
下图是l=500,s1=3,a=0.90,0.94,0.98的情形
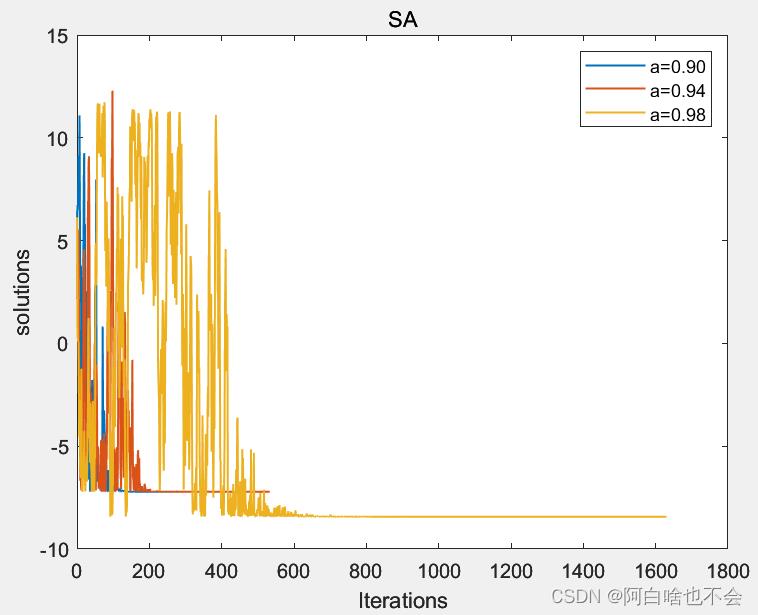
总结(summmary)
模拟退火算法由于对旧解的处理使它能更大概率跳出局部最优解,但在运用的时候要进行调参记录相应的最优解,最后横向比较即可得出最优解。
以上是关于阿白数模笔记之模拟退火算法(simulated annealing,SA)的主要内容,如果未能解决你的问题,请参考以下文章