attack on titans(动态规划递推,限制条件,至少转至多方法,进击的巨人)

Posted 2021-01-18 zyacmer

题目意思：

给n个士兵排队，每个士兵三种G、R、P可选，求至少有m个连续G士兵，最多有k个连续R士兵的排列的种数。

原题

Attack on Titans

Time Limit: 2 Seconds Memory Limit: 65536 KB

 

Over centuries ago, mankind faced a new enemy, the Titans. The difference of power between mankind and their newfound enemy was overwhelming. Soon, mankind was driven to the brink of extinction. Luckily, the surviving humans managed to build three walls: Wall Maria, Wall Rose and Wall Sina. Owing to the protection of the walls, they lived in peace for more than one hundred years.

But not for long, a colossal Titan appeared out of nowhere. Instantly, the walls were shattered, along with the illusory peace of everyday life. Wall Maria was abandoned and human activity was pushed back to Wall Rose. Then mankind began to realize, hiding behind the walls equaled to death and they should manage an attack on the Titans.

So, Captain Levi, the strongest ever human being, was ordered to set up a special operation squad of N people, numbered from 1 to N. Each number should be assigned to a soldier. There are three corps that the soldiers come from: the Garrison, the Recon Corp and the Military Police. While members of the Garrison are stationed at the walls and defend the cities, the Recon Corps put their lives on the line and fight the Titans in their own territory. And Military Police serve the King by controlling the crowds and protecting order. In order to make the team more powerful, Levi will take advantage of the differences between the corps and some conditions must be met.

The Garrisons are good at team work, so Levi wants there to be at least M Garrison members assigned with continuous numbers. On the other hand, members of the Recon Corp are all elite forces of mankind. There should be no more than K Recon Corp members assigned with continuous numbers, which is redundant. Assume there is unlimited amount of members in each corp, Levi wants to know how many ways there are to arrange the special operation squad.

Input

There are multiple test cases. For each case, there is a line containing 3 integers N (0 < N < 1000000), M (0 < M < 10000) and K (0 < K < 10000), separated by spaces.

 

Output
One line for each case, you should output the number of ways mod 1000000007.

Sample Input

3 2 2

Sample Output
5

 

 

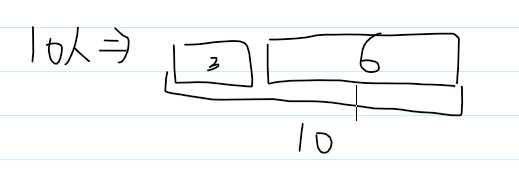
//首先感谢MartaYang的详细博文让我搞懂这题
//https://blog.csdn.net/MartaYang/article/details/77175488
/*
思路:
1(至少化为至多):至少化为至多,这样可以使问题简单化,
比如说从10个人中至少挑3人=10人至多挑十人(无限制的总方案数)-10人至多挑6人

 

那么这题同理有:
至少m个连续G士兵=至多n个连续G士兵-至多m-1个连续G士兵

准备一个数组,纵行代表处理到第几位放哪个士兵的方案数,横行代表这三个兵种各自的方案数
先处理一下边缘条件,然后
假设G至多u个连续,R至多v个连续(刚刚已经把至少问题转换为至多问题了)
对于G:
如果现在当前行i<=u,那么可以随便排列

 

如果当前行i=u+1,加完各种情况后要减去一种情况,就是前面u个全是g的情况,
因为是一种情况,所以减1

 

如果当前行>u+1,那么加完各种情况后要-a[i-u-2]-a[i-u-3];
即减去第i-u-2位不是G而中间其他位置都是G的情况,这样可以避免第i个放下去后产生u+1个连续
有人会问为什么不是-1-1
因为这其实是-a[i-u-2]*1-a[i-u-3]*1
那个*1其实是*中间全是G,这却时常是1种,所以-a[i-u-2]-a[i-u-3]

 

用这种方法,i>u+1位以后,就不可能出现连续数超过u,因为通过减方案减去了可能出现问题的地方
*/
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll maxn=10e6+10;
ll a[maxn][4];//定义一个数组,a[i][1]代表第i位选的总方案数G士兵,
//同理a[i][2]代表第i位选R士兵的总方案数,a[i][1]代表第i位选P士兵的总方案数,
ll n,m,k;//最少m个连续G,最多k个连续R
ll mod=1000000007;//定义模,题目要求取模
ll solve(ll u,ll v)//准备一个函数算方案
{
    if(u==0) a[1][1]=0; else a[1][1]=1;//为G士兵赋初始值,要考虑当连续的要求为0的情况
    //a[1][1]表示第一位选G的方案数
    //a[2][1]表示第二位选G并且包含前面的总方案数
    if(v==0) a[1][2]=0;else a[1][2]=1;//v和u差不多
    a[1][3]=1;//第三种士兵没有限制,直接赋初值为1
    for(ll i=2;i<=n;i++)//枚举每一个位置,从2到n
    {
        a[i][3]=a[i-1][1]+a[i-1][2]+a[i-1][3];
        //第三种士兵的方案数等于前一个位置三种方案数相加
        if(i<=u) a[i][1]=(a[i-1][1]+a[i-1][2]+a[i-1][3])%mod;
        else if(i==u+1) a[i][1]=(a[i-1][1]+a[i-1][2]+a[i-1][3]-1)%mod;
        else a[i][1]=(a[i-1][1]+a[i-1][2]+a[i-1][3]-a[i-u-1][2]-a[i-u-1][3])%mod;

        if(i<=v) a[i][2]=(a[i-1][1]+a[i-1][2]+a[i-1][3])%mod;
        else if(i==v+1) a[i][2]=(a[i-1][1]+a[i-1][2]+a[i-1][3]-1)%mod;
        else a[i][2]=(a[i-1][1]+a[i-1][2]+a[i-1][3]-a[i-u-1][1]-a[i-u-1][3])%mod;
    }
    return (a[n][1]+a[n][2]+a[n][3])%mod;//把方案数return出去

}

int main()
{
    cin>>n>>m>>k;
    //最多n个连续G,最多k个连续R --减去-- 最少m-1个连续G,最多k个连续R
    cout<<((solve(n,k)-solve(m-1,k))%mod+mod)%mod<<endl;
    return 0;
}