HDU - 5628：Clarke and math （组合数&线性筛||迪利克雷卷积）

Posted 2021-01-18 hua-dong

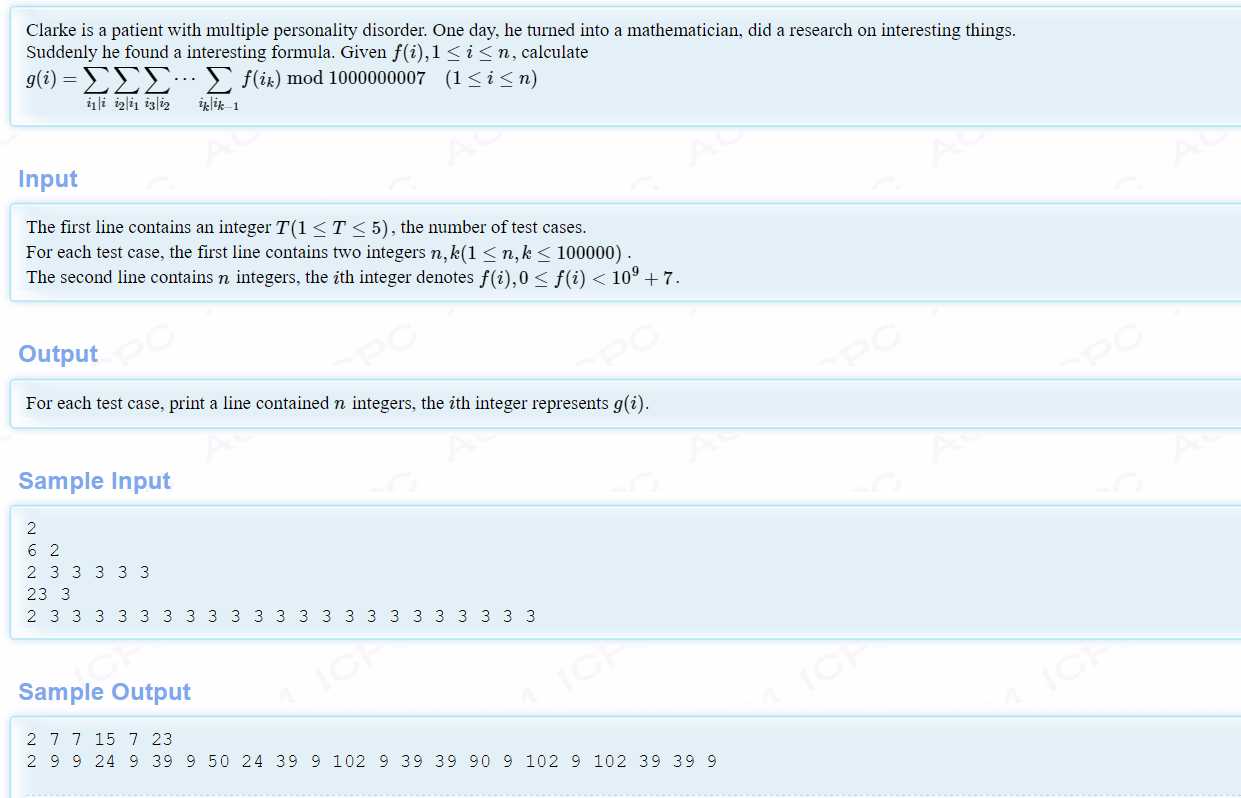
题意：略。

思路：网上是用卷积或者做的，不太会。 因为上一题莫比乌斯有个类似的部分，所以想到了每个素因子单独考虑。

我们用C(x^p)表示p次减少分布在K次减少里的方案数，由隔板法可知，C(x^p)=C(K+p-1,K-1);  而且满足C(x)有积性，即gcd(x,y)==1时，有C(x*y)=C(x)*C(y);

所以C数组可以线性筛。 把筛素数的线性筛，稍微改一下即可，low[i]代表的是i的最小素数因子x的p次方，即x^p|i，p最大，num[i]代表的是幂次p。

那么g(x)=Σ f(a)*C(x/a)； g数组也可以线性筛。这里相当于手动卷积。

所以C和g函数分别线性筛即可。

#include<bits/stdc++.h>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define ll long long
using namespace std;
const int maxn=100010;
const int Mod=1e9+7;
int rev[maxn],f[maxn],ans[maxn],jc[maxn],fz[maxn],p[maxn];
int vis[maxn],low[maxn],num[maxn],C[maxn],cnt,N,K;
int qpow(int a,int x){
    int res=1; while(x){
        if(x&1) res=(ll)res*a%Mod;
        a=(ll)a*a%Mod; x>>=1;
    } return res;
}
void getC()
{
    cnt=0; rep(i,1,maxn) low[i]=num[i]=0;
    for(int i=2;i<maxn;i++){
        if(!vis[i]) p[++cnt]=i,low[i]=i,num[i]=1;
        for(int j=1;j<=cnt&&i*p[j]<maxn;j++){
            vis[i*p[j]]=1;
            if(i%p[j]==0){
                low[i*p[j]]=low[i]*p[j];
                num[i*p[j]]=num[i]+1;
                break;
            }
            low[i*p[j]]=p[j];
            num[i*p[j]]=1;
        }
    }
}
int main()
{
    jc[0]=1;rep(i,1,maxn-1) jc[i]=(ll)jc[i-1]*i%Mod;
    rev[maxn-1]=qpow(jc[maxn-1],Mod-2);
    for(int i=maxn-2;i>=0;i--) rev[i]=(ll)rev[i+1]*(i+1)%Mod;
    getC();
    int T; scanf("%d",&T);
    while(T--){
        scanf("%d%d",&N,&K);
        fz[0]=1; rep(i,1,N) fz[i]=(ll)fz[i-1]*(i+K-1)%Mod,ans[i]=0;
        rep(i,1,N) scanf("%d",&f[i]);
        C[1]=1;
        rep(i,2,N) C[i]=(ll)C[i/low[i]]*rev[num[i]]%Mod*fz[num[i]]%Mod;
        for(int i=1;i<=N;i++){
         for(int j=i;j<=N;j+=i)
            (ans[j]+=(ll)f[i]*C[j/i]%Mod)%=Mod;
        }
        rep(i,1,N-1) printf("%d ",ans[i]);
        printf("%d
",ans[N]);
    }
    return 0;
}

 到此，引申一下有个题，给定N<1e7，K<1e9，求1^K+2^K+3^+...N^K。

这里由于K过大，显然不能用拉格朗日插值法。 我们用线性筛来做，如果i是素数，我们就快速幂求f[i]=i^K，否则就用之前的结果就好了，即f[i]=f[low[i]]^f[i/low[i]];

由于素数的个数大约=N/lgN; 而快速幂的复杂度是lgK。所以整个算法差不多是线性的。