回朔法之应用1

Posted 2021-01-18 zf-blog

题目链接：https://www.nowcoder.com/practice/8fecd3f8ba334add803bf2a06af1b993?tpId=13&tqId=11185&tPage=2&rp=2&ru=%2Fta%2Fcoding-interviews&qru=%2Fta%2Fcoding-interviews%2Fquestion-ranking

题目描述：

析：这道题的解空间其实是一个“排列树”，比如输入是{3 ， 32 ， 321}时，排列树如下：

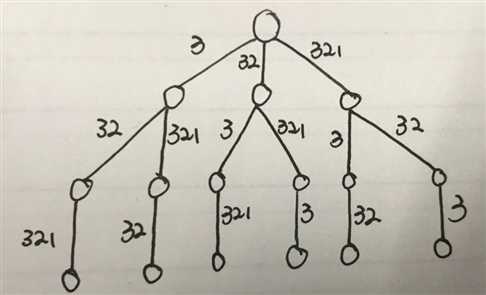
所以可以考虑使用回朔法解决。再次回顾一下回朔法的思想：从根节点开始一层一层向下扩展，当扩展到“非扩展节点”时则回溯到上一层，在进行“约束条件”（路径合理性）和“上界条件”（路径最优性，实现剪枝功能）的判断，如果满足则从该节点的另一条路径继续向下，否则继续回溯，就是这样一个递归算法；详细解释可以参考：https://www.cnblogs.com/zf-blog/p/8973051.html

代码如下：

#include<iostream>
#include<string>
#include<vector>
#include<cmath>

using namespace std;

long long min = 0;  //最小数
int n = 0;  //排列树的深度（从0开始）
long long current = 0;  //到达某一节点时的值
vector<long long> x;  //最优解中数组元素的排列

long long m_1(vector<long long> sub, vector<long long> numbers)  //为了计算到达某一节点时的值
{
    int count = 0;
    for (int i = 0; i < numbers.size(); i++)
    {
        long long tmp = numbers[i];
        bool flag = false;  //不包含
        for (int j = 0; j < sub.size(); j++)
        {
            if (tmp == sub[j])
            {
                flag = true;
                break;
            }
        }
        if (flag == false)
        {
            if (numbers[i] == 0)
                count++;
            else
            {
                while (numbers[i] % 10)
                {
                    count++;
                    numbers[i] /= 10;
                }
            }
        }
    }
    return pow(10 , count);
}

void Backtrack(int t)  //回溯算法
{
    if (t >= n)
    {
        current = 0;
        string current_str = "";
        for (int i = 0; i < n; i++)
        {
            string tmp = to_string(x[i]);
            current_str.append(tmp);
        }
        current = atoll(&current_str.at(0));
        if (current < min)
            min = current;
        return;

    }
    for (int i = t; i < n; i++)
    {
        swap(x[t], x[i]);
        vector<long long> tmp;
        for (int j = 0; j <= t; j++)
        {
            tmp.push_back(x[j]);
        }
        long long m_2 = m_1(tmp, x);
        string current_str = "";
        for (int m = 0; m < tmp.size(); m++)
        {
            string tmp_str = to_string(tmp[m]);
            current_str.append(tmp_str);
        }
        current = atoll(&current_str.at(0)) * m_2;
        if (current < min)
        {
            Backtrack(t + 1);
        }
        swap(x[t], x[i]);
    }
}
string PrintMinNumber(vector<long long> numbers) {
    n = numbers.size();
    string min_str = "";
    for (int i = 0; i < n; i++)
    {
        x.push_back(numbers[i]);
        string tmp = to_string(numbers[i]);
        min_str.append(tmp);
    }
    min = atoll(&min_str.at(0));
    Backtrack(0);
    string output = to_string(min);
    return output;
}

int main(int argc, char *argv[])
{
    vector<long long> numbers(3);
    long long a[3] = { 12 , 33 , 4 };
    for (int i = 0; i < 3; i++)
    {
        numbers[i] = a[i];
    }
    string output = PrintMinNumber(numbers);
    cout << output << endl;

    system("pause");
    return 0;
}

 

PS：该算法在VS上验证OK，在牛客网自带的编译器中会出错，属于编译问题；