平时二十四测

Posted 2021-01-18 edsheeran

今天都是思维题

题解：

第一题:https://www.cnblogs.com/mlystdcall/p/6645725.html

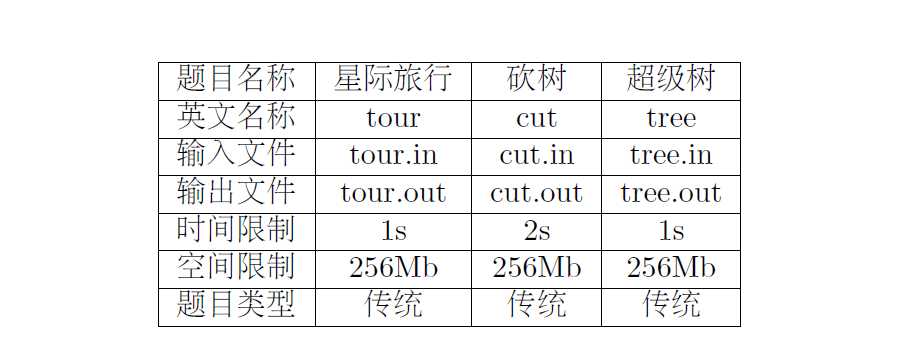
首先图不连通的时候肯定答案是0，我们下面讨论图联通的情况

首先考虑，如果我们每条边都经过两边，那么肯定是可行的

因为这样相当于把每条边复制一遍，然后问图中是否存在欧拉路径

既然每条边都出现了两遍，那么所有点的度数一定都是偶数，所以肯定有欧拉路径

现在考虑将某两条边变成出现一遍，这样的话可能会有一些点的度数变成奇数

如果我们把两条非自环的边变成出现一遍，并且这两条边不交于同一个点，那么就会有四个度数为奇数的点，则图中不存在欧拉路径

如果我们把两条非自环的边变成出现一遍，并且这两条边交于同一个点，那么就会有两个度数为奇数的点，存在欧拉路径

如果我们把两条自环边变成出现一遍，所有点的度数仍然为偶数，存在欧拉路径

如果我们把一条自环，一条非自环的边变成出现一遍，那么就会有两个度数为奇数的点，存在欧拉路径

所以一共就几种情况，除去判联通的部分，我们只要记录每个点的度数（不含自环）和自环的数量就好了

因为题目中保证一条边不会出现两遍，所以我们的方法才是可行的

 维护联通性是边联通，不是点联通

#include<bits/stdc++.h>
using namespace std;
const int M = 1e6 + 5;
int deg[M], loop, fa[M], l[M];
int find(int x){return fa[x] == x ? x : fa[x] = find(fa[x]);}


int main(){
    freopen("tour.in","r",stdin);
    freopen("tour.out","w",stdout);
    int n, m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) fa[i]=i;
    for(int i=1;i<=m;i++){
        int v;
        scanf("%d%d",&l[i],&v);
        fa[find(l[i])]=find(v);
        if(l[i]==v)loop++;
        else deg[l[i]]++,deg[v]++;
    }
    int lst=find(l[1]);
    for(int i=2;i<=m;i++) 
        if(find(l[i]) != lst) return !puts("0");
    long long ans=1LL*loop*(loop-1)/2 + 1LL*(m-loop)*loop;
    for(int i=1;i<=n;i++){
        ans+=1LL*deg[i]*(deg[i]-1)/2;
    }
    printf("%lld
",ans);
}

View Code

 

 

第二题：原题，见：https://www.cnblogs.com/EdSheeran/p/9530002.html

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int M = 1e7;
int a[105], tot, n;
ll yz[M], k;
bool vis[M];
void chai(int x){
    for(int d = x; d > 0; ){
        int fm = (x + d - 1) / d;
        int nw = (x + fm - 1) / fm;
        if(fm < 1e6 && !vis[fm]){
            yz[++tot] = fm;
            vis[fm]=1;
        }
        else yz[++tot] = fm;
        d = nw - 1;
    }
}

bool check(ll now){
    ll ans = 0;
    for(int i = 1; i <= n; i++)
        ans = ans + 1LL*(a[i] + now - 1)/now * now - a[i];
    return ans <= k;
}


int main(){
    freopen("cut.in","r",stdin);
    freopen("cut.out","w",stdout);
    scanf("%d%lld", &n, &k);
    for(int i = 1; i <= n; i++){
        scanf("%d", &a[i]);        
        chai(a[i]);
        k += a[i];
    }
    ll ans = -1;
    yz[++tot] = 1e12;
    sort(yz + 1, yz + 1 + tot);
    tot = unique(yz + 1, yz + 1 + tot) - yz - 1;
    for(int i = 1; i <= tot; i++){
        ll cur = 0;
        for(int j = 1; j <= n; j++)
            cur = cur + 1LL*(a[j] + yz[i] - 1)/yz[i];
        ll mx = k/cur;
        if(mx>=yz[i]) ans = max(ans, mx);
    }
    printf("%lld
", ans);
}

View Code

 

 

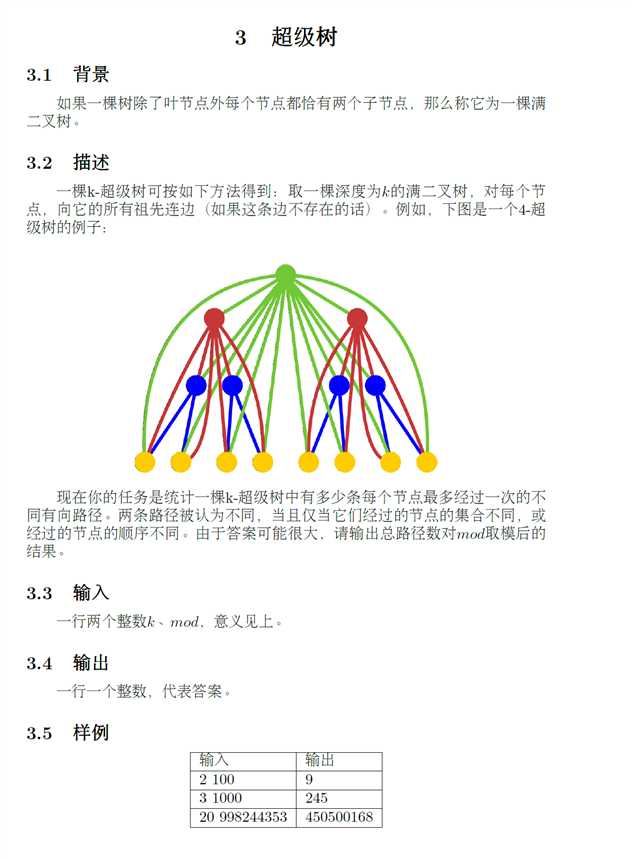
第三题：

 

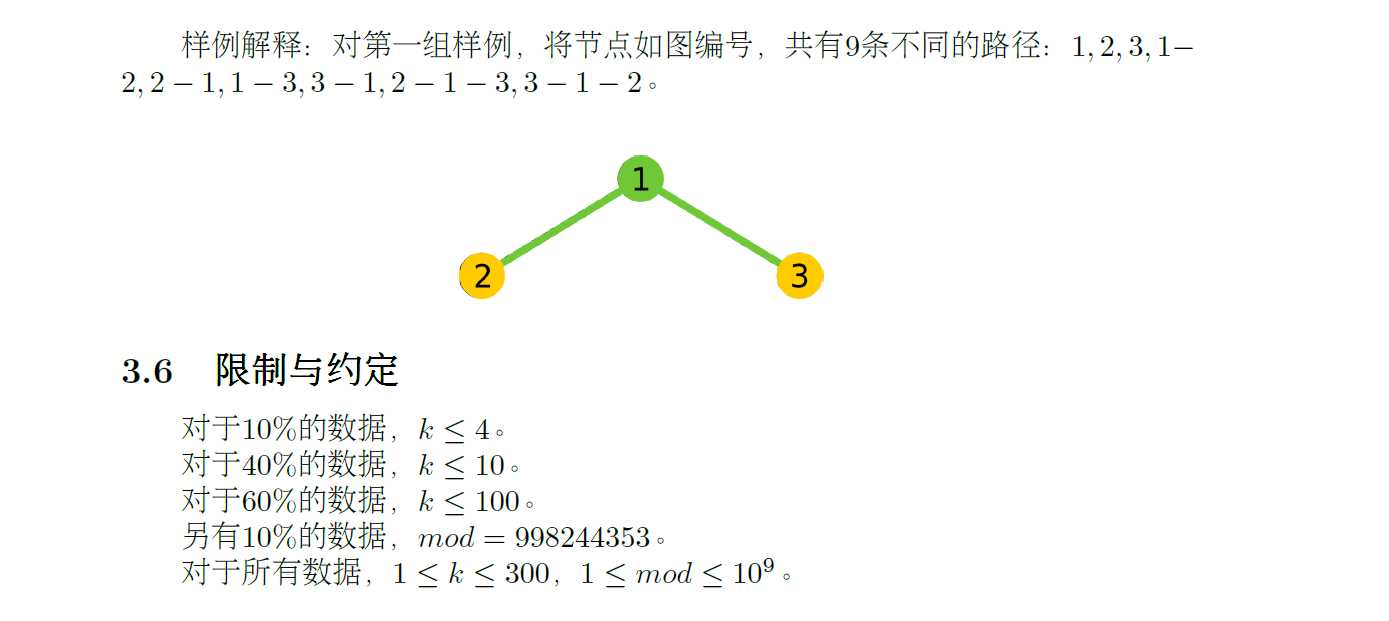
这题*2是因为新加的点可以作为起点或者终点，所以图中的边记录的都是有向的

#include<bits/stdc++.h>
using namespace std;

#define ll long long
ll dp[305][305], mod;
inline void up(ll &a, ll b){
    a += b; if(a >= mod) a -= mod;
}

int main(){
    freopen("tree.in","r",stdin);
    freopen("tree.out","w",stdout);
    int n;
    cin>>n>>mod;
    dp[1][0] = dp[1][1] = 1;
    for(int i=2;i<=n;i++){
        int lim=n-i+2;
        for(int l=0;l<=lim;l++)
            for(int r=0;r+l-1<=lim;r++){
                ll num=dp[i-1][l]*dp[i-1][r]%mod;
                up(dp[i][l+r], num);
                up(dp[i][l+r+1], num);
                up(dp[i][l+r], num*(l+r)*2%mod);
                if(l+r){
                    up(dp[i][l+r-1], num*l*r*2%mod);
                    up(dp[i][l+r-1], num*(l*(l-1)+r*(r-1))%mod);
                }
                
            }
    }
    printf("%lld
", dp[n][1]%mod);
}

View Code