平衡树

Posted 2021-01-18 zuofaqi

二叉树查找效率很高，但是它有一个缺点。类似下面一棵树，查找效率是线性的：

定义

于是，引出了平衡二叉树(Self-balancing binary search tree)，也叫 BTree(balance tree)，AVLTree

它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

使用它，查找效率肯定是 O(log n)。不过，为了保持树的性质，增添和删除节点的时候，需要做额外的旋转操作，这会牺牲掉 O(log n) 的时间

旋转

分为4中情况

1.左左旋转

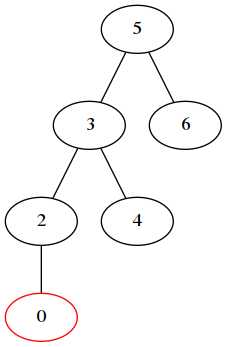
5 节点失去了平衡，因为在左子树增加的一个新节点 0，0 在左子树 3 的左孩子上增加的，需要左左旋转，旋转的结果为：

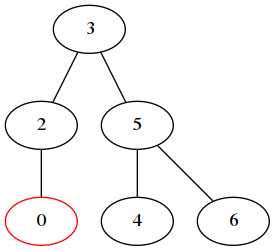
2. 右右旋转

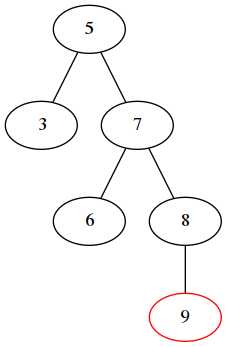
9 是在右子树的右子树增加的节点，导致数不平衡，右右旋转：

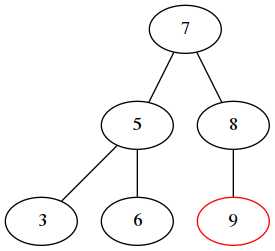
3. 左右旋转

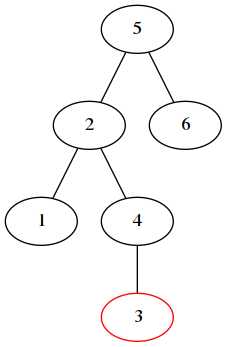
新增的3节点，在左子树的右子树上。需要两次旋转，以2为根，做右右旋转，再以5为根做左左旋转：

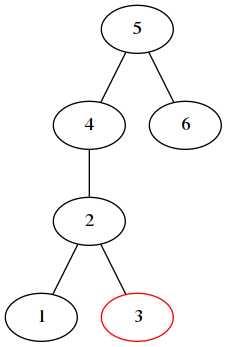
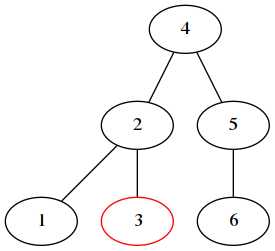
4. 右左旋转，先右旋转，再左旋转。不画图了

下面是代码，为了方便观察，使用了graphviz画图，需要安装，保存的文件名为：当前目录的tree.png，

如果没有安装graphviz，注释掉 tree.draw() 

#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>

#include <queue>
#include <list>


template <typename T>
struct stTreeNode
{
    T               d;
    int             height;
    stTreeNode<T>  *left;
    stTreeNode<T>  *right;

    stTreeNode(T data):d(data),left(NULL),right(NULL) {}
};

template <typename T>
class CBTree
{
public:
    typedef T                           value_type;
    typedef T*                          value_pointer;
    typedef T&                          value_reference;
    typedef const T&                    const_value_reference;
    typedef stTreeNode<T>               node_type;
    typedef node_type*                  node_pointer;

public:
    CBTree():root(NULL) {}
    CBTree(value_pointer arr, int len);

    void    insertData(const_value_reference data) { _insertData(&root, data); }
    void    deleteData(const_value_reference data) { _deleteData(&root, data); }

    void    preorderTravel() { _preorderTravel(root); }
    void    inorderTravel() { _inorderTravel(root); }

    void    draw();

private:
    node_pointer    root;

private:
    int     getHeight(node_pointer node);
    void    LL(node_pointer *node);
    void    LR(node_pointer *node);
    void    RR(node_pointer *node);
    void    RL(node_pointer *node);
    void    _insertData(node_pointer *node, const_value_reference data);
    void    _deleteData(node_pointer *node, const_value_reference data);

    void    _preorderTravel(node_pointer root);
    void    _inorderTravel(node_pointer root);
};

template <typename T>
void CBTree<T>::_inorderTravel(node_pointer root)
{
    if (root)
    {
        _inorderTravel(root->left);
        std::cout << root->d << " ";
        _inorderTravel(root->right);
    }
}

template <typename T>
void CBTree<T>::_preorderTravel(node_pointer root)
{
    if (root)
    {
        std::cout << root->d << " ";
        _preorderTravel(root->left);
        _preorderTravel(root->right);
    }
}

template <typename T>
CBTree<T>::CBTree(value_pointer arr, int len)
{
    root = NULL;

    for (int i = 0; i < len; ++i)
    {
        _insertData(&root, arr[i]);
    }
}

template <typename T>
int CBTree<T>::getHeight(node_pointer node)
{
    return node == NULL ? 0 : node->height;
}

template <typename T>
void CBTree<T>::LL(node_pointer *node)
{
    node_pointer q = (*node)->left;
    (*node)->left = q->right;
    q->right = *node;
    (*node)->height = (getHeight((*node)->left) > getHeight((*node)->right) ? getHeight((*node)->left) : getHeight((*node)->right)) + 1;
    q->height = (getHeight(q->left) > getHeight(q->right) ? getHeight(q->left) : getHeight(q->right)) + 1;
    *node = q;
}

template <typename T>
void CBTree<T>::RR(node_pointer *node)
{
    node_pointer q = (*node)->right;
    (*node)->right = q->left;
    q->left = *node;
    (*node)->height = (getHeight((*node)->left) > getHeight((*node)->right) ? getHeight((*node)->left) : getHeight((*node)->right)) + 1;
    q->height = (getHeight(q->left) > getHeight(q->right) ? getHeight(q->left) : getHeight(q->right)) + 1;
    *node = q;
}

template <typename T>
void CBTree<T>::LR(node_pointer *node)
{
    RR(&(*node)->left);
    LL(node);
}

template <typename T>
void CBTree<T>::RL(node_pointer *node)
{
    LL(&(*node)->right);
    RR(node);
}

template <typename T>
void CBTree<T>::_insertData(node_pointer *node, const_value_reference data)
{
    if (*node == NULL)
    {
        *node = new node_type(data);
        (*node)->height = 1;
    }
    else if (data < (*node)->d)
    {
        _insertData(&(*node)->left, data);
        if (getHeight((*node)->left) - getHeight((*node)->right) > 1)
        {
            node_pointer left = (*node)->left;
            if (getHeight(left->left) > getHeight(left->right))
            {
                LL(node);
            }
            else
            {
                LR(node);
            }
        }
        (*node)->height = (getHeight((*node)->left) > getHeight((*node)->right) ? getHeight((*node)->left) : getHeight((*node)->right)) + 1;
    }
    else
    {
        _insertData(&(*node)->right, data);
        if (getHeight((*node)->right) - getHeight((*node)->left) > 1)
        {
            node_pointer right = (*node)->right;
            if (getHeight(right->right) > getHeight(right->left))
            {
                RR(node);
            }
            else
            {
                RL(node);
            }
        }
        (*node)->height = (getHeight((*node)->left) > getHeight((*node)->right) ? getHeight((*node)->left) : getHeight((*node)->right)) + 1;
    }
}

template <typename T>
void CBTree<T>::_deleteData(node_pointer *node, const_value_reference data)
{
    if (*node != NULL)
    {
        if (data == (*node)->d)
        {
            // 左子树深度大，把左子树最大值补过来
            if ((*node)->left && getHeight((*node)->left) >= getHeight((*node)->right))
            {
                node_pointer tmp = (*node)->left;
                node_pointer parent = (*node)->left;

                while (tmp->right != NULL)
                {
                    parent = tmp;
                    tmp = tmp->right;
                }
                (*node)->d = tmp->d;
                // (*node)->left是叶子节点
                if (parent == tmp)
                {
                    delete (*node)->left;
                    (*node)->left = NULL;
                }
                else
                {
                    parent->right = tmp->left;
                    delete tmp;
                }
            }
            // 右子树深度大，把右子树最小值补过来
            else if ((*node)->right && getHeight((*node)->left) < getHeight((*node)->right))
            {
                node_pointer tmp = (*node)->right;
                node_pointer parent = (*node)->right;

                while (tmp->left != NULL)
                {
                    parent = tmp;
                    tmp = tmp->left;
                }
                (*node)->d = tmp->d;

                if (parent == tmp)
                {
                    delete (*node)->right;
                    (*node)->right = NULL;
                }
                else
                {
                    parent->left = tmp->right;
                    delete tmp;
                }
            }
            // 要删除的节点是叶子节点
            else
            {
                delete *node;
                *node = NULL;
            }
        }
        else if (data < (*node)->d)
        {
            _deleteData(&(*node)->left, data);
        }
        else
        {
            _deleteData(&(*node)->right, data);
        }

        // 调整
        if (*node)
        {
            if (getHeight((*node)->left) - getHeight((*node)->right) > 1)
            {
                node_pointer left = (*node)->left;
                if (getHeight(left->left) > getHeight(left->right))
                {
                    LL(node);
                }
                else
                {
                    LR(node);
                }
            }
            else if (getHeight((*node)->right) - getHeight((*node)->left) > 1)
            {
                node_pointer right = (*node)->right;
                if (getHeight(right->right) > getHeight(right->left))
                {
                    RR(node);
                }
                else
                {
                    RL(node);
                }
            }
        }

        if (*node)
        {
            (*node)->height = 1 + (getHeight((*node)->left) > getHeight((*node)->right) ?  getHeight((*node)->left) : getHeight((*node)->right));
        }
    }
}

template <typename T>
void CBTree<T>::draw()
{
    std::queue<node_pointer, std::list<node_pointer> > Q;
    if (root)
    {
        Q.push(root);
    }
    
    FILE *pf = fopen("bt.dot", "w+");
    if (pf)
    {
        fprintf(pf, "graph btree {
");

        while (!Q.empty())
        {
            node_pointer node = Q.front();
            Q.pop();
            if (node->left)
            {
                fprintf(pf, "	%d -- %d[color="red"];
", node->d, node->left->d);
                Q.push(node->left);
            }
            if (node->right)
            {
                fprintf(pf, "	%d -- %d[color="blue"];
", node->d, node->right->d);
                Q.push(node->right);
            }
        }

        fprintf(pf, "}
");
        fclose(pf);
    }
    system("dot bt.dot -Tpng -o tree.png");
}

int main()
{
    int arr[] = {23,5,6,1,3,2,34,67,12,52,82,31,78,95};
    int len = sizeof(arr)/sizeof(int);

    CBTree<int> tree(arr, len);
    tree.insertData(98);
    tree.insertData(99);
    tree.insertData(10);

    tree.deleteData(99);
    tree.deleteData(95);
    tree.deleteData(6);
    // tree.deleteData(2);
    // tree.deleteData(5);
    // tree.deleteData(12);
    // tree.deleteData(78);
    // tree.deleteData(34);
    // tree.deleteData(67);
    // tree.deleteData(98);
    // tree.deleteData(6);

    tree.draw();

    return 0;
}