归并排序

Posted 2021-01-17 naloy

原理

归并排序（merge sort）采用经典的分治策略，将两个有序的数列合并成一个大的有序的序列，通过递归，层层合并。

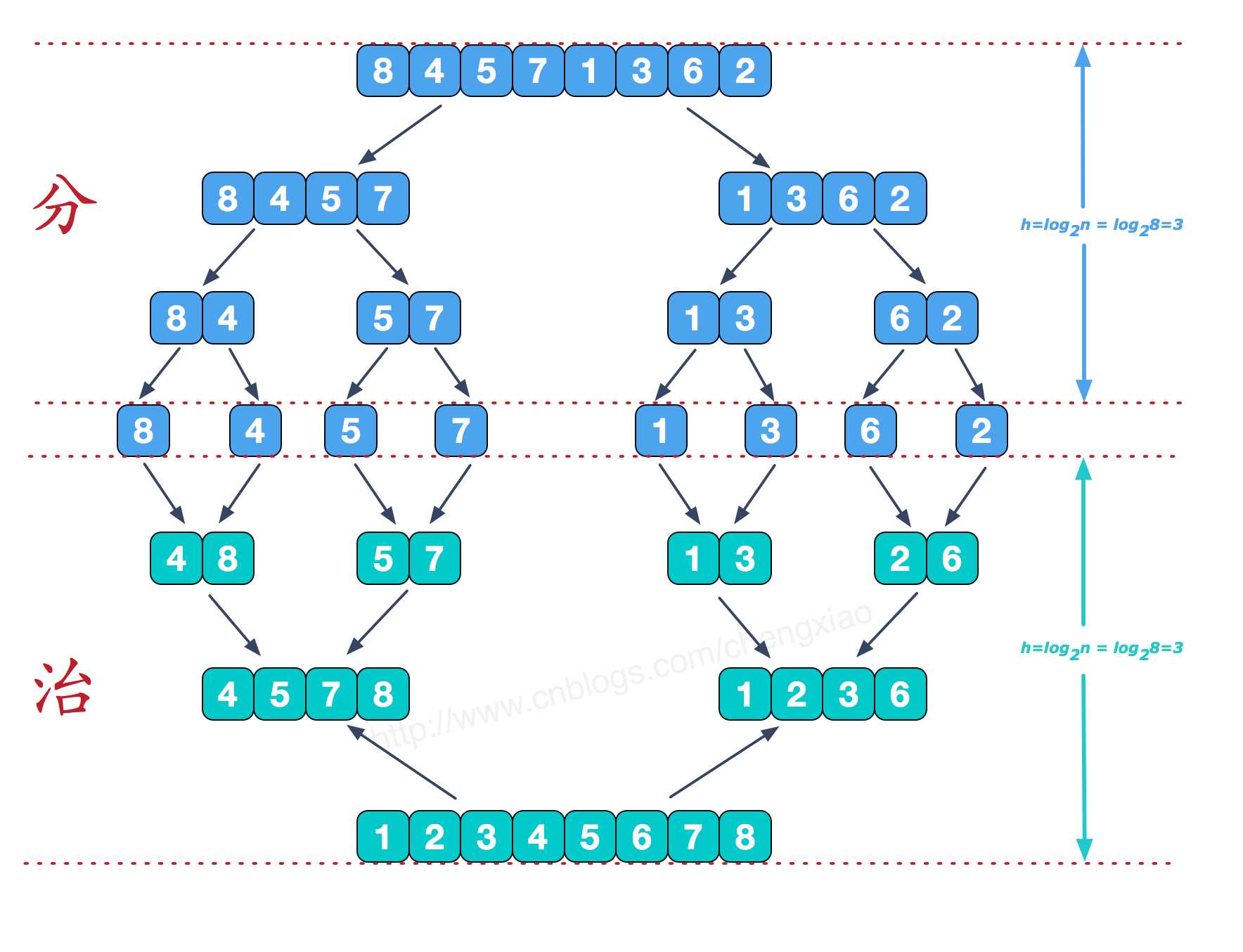
流程

对于两个有序的序列合成一个有序的序列，比如 要将 【4,5,7,8】和【1,2,3,6】最终合成【1,2,3,4,5,6,7,8】

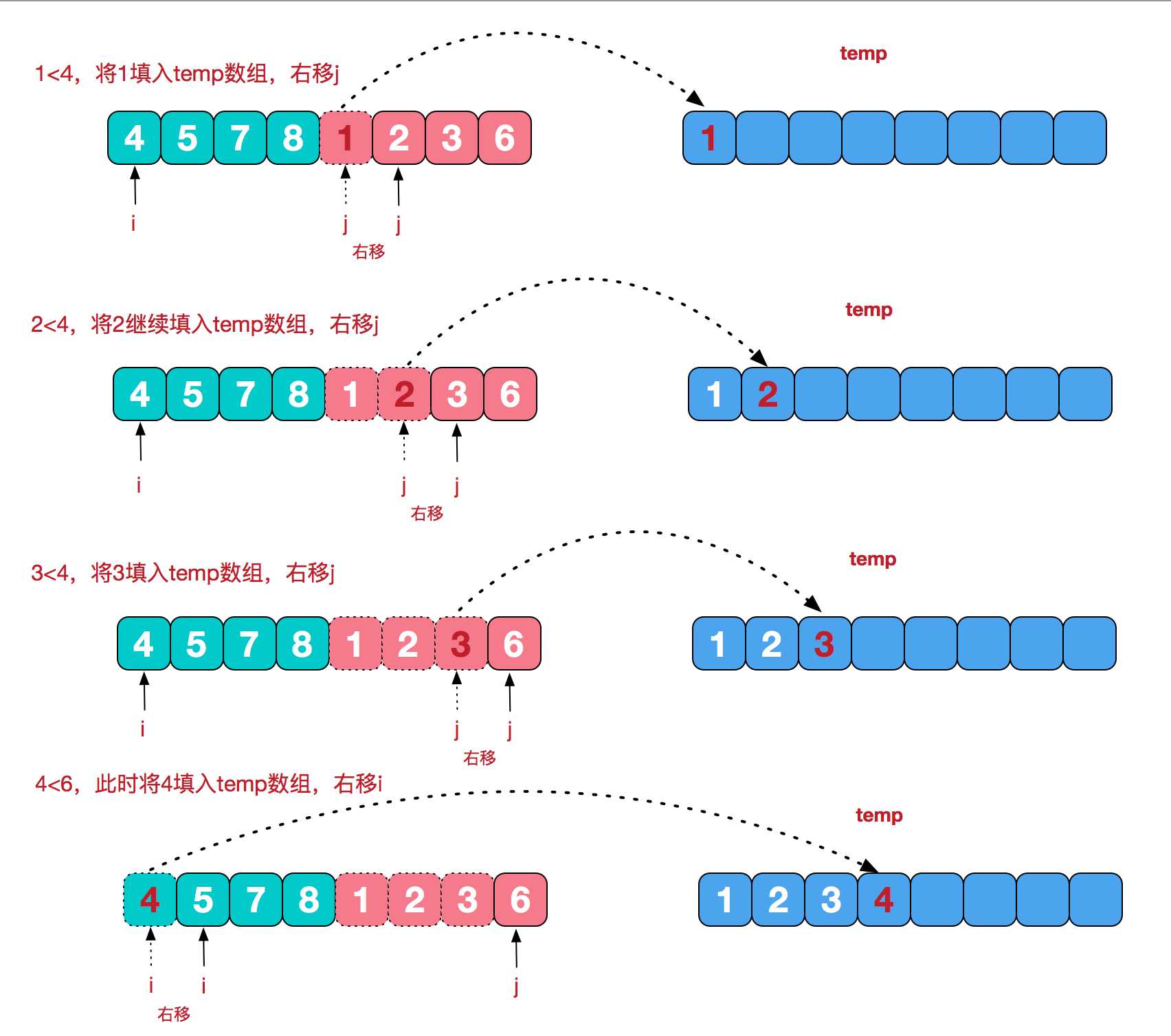
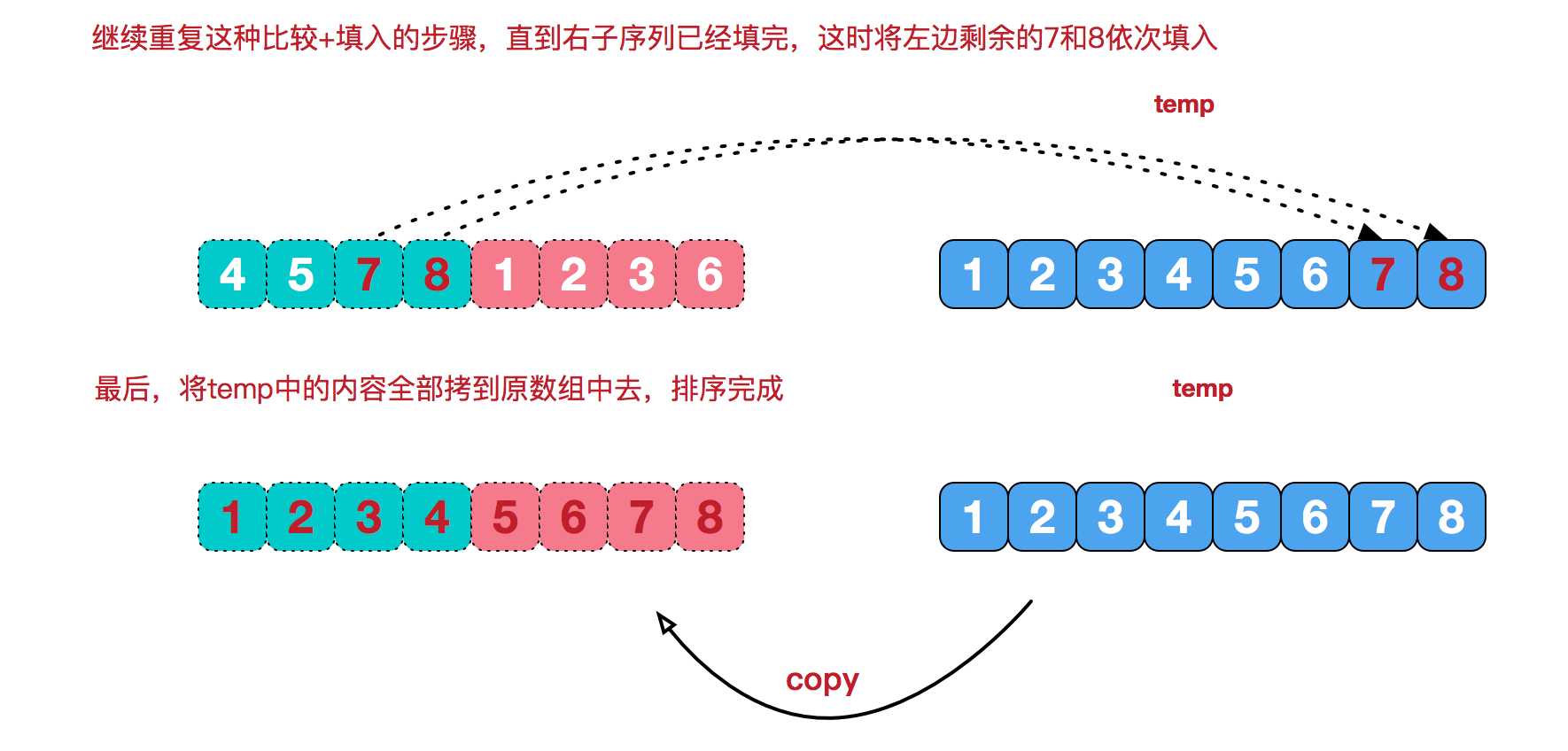
代码

package sequence;

import java.util.Arrays;

/**
 * 归并排序
 */
public class MergeSort {

    public static void mergeSort(int[] arr){

        //参数校验
        if(arr == null || arr.length<2){
            return;
        }
        sortProcess(arr,0,arr.length-1);
    }

    /**
     * 排序过程
     * @param arr 要排序的数组
     * @param L 左下标
     * @param R 右下标
     */
    public static void sortProcess(int[] arr,int L,int R){

        //只有一个数
        if(L == R){
            return;
        }

        //中间位置
        int mid = L +((R-L)>>1);
        //左边归并排序，使得左子序列有序
        sortProcess(arr,L,mid);
        //右边归并排序，使得右子序列有序
        sortProcess(arr,mid+1,R);
        //外排，合并操作
        merge(arr,L,mid,R);

    }

    /**
     * 两个有序序列合并
     * @param arr 原数组
     * @param L 左序列的起始位置
     * @param mid 左序列的结束位置
     * @param R 右序列的结束位置
     */
    public static void merge(int[] arr,int L,int mid,int R){
        int[] temp = new int[R-L+1];
        int k = 0; //temp 数组下标
        int i = L; // 指向左序列起始位置 如图中 i 指向的4
        int j = mid+1; //指向右序列起始位置 如图中 j 指向1

        //哪个指针指向的数小，哪个数就填入temp 数组，然后指针继续移动
        while (i <= mid && j <= R){
            temp[k++] = arr[i] < arr[j] ? arr[i++] : arr[j++];
        }

        // j 越界 把左序列剩下的元素填入temp
        while (i <= mid){
            temp[k++] = arr[i++];
        }

        // i 越界，把右序列剩下的元素填入temp
        while (j <= R){
            temp[k++] = arr[j++];
        }

        //将temp数组中的元素拷贝到原数组中
        System.arraycopy(temp,0,arr,L,temp.length);

    }


    public static void main(String[] args) {
        int[] arr = {8,4,5,7,1,3,6,2};
        mergeSort(arr);
        System.out.println(Arrays.toString(arr));
    }

}

复杂度

归并排序是稳定排序，它也是一种十分高效的排序,对于复杂度的计算可以使用master 公式，

递归master公式

T(N)的公式从大规模来看，不细分。
T(N) = a * T(N/b)+O(n^d)
N/b 是子过程数据量 ；a是子过程调用多少次；O(n^d)是除去过程之外剩下的数据量的多少
if log( b^a ) > d => O( N^{log(b^a)} )
if log( b^a ) = d => O( N^d *logN)
if log( b^a ) < d => O( N^d )
注意 多个递归的规模必须一样，否则master公式失效。

计算复杂度

1、我们设sortProcess的时间复杂度为T(N) 
2、从宏观上看，他分别调用了两次自己的函数sortProcess和一次merge,那么T(N)等于两次mergeSort的时间复杂度和一次merge的时间复杂度 
3、调用自己的函数的时候，函数个数为N/2，则T(N)=2*T(N/2)+一次merge的时间复杂度 
4、根据上面的流程分析merge总共扫描了N个数，执行了N次，所以时间复杂度为O(N) 
5、所以T(N)=2*(N/2)+O(N) 
6、根据Master公式，此时a=2,b=2,d=1,满足log(b,a) = d 
7、所以归并排序时间复杂度为：O(N^d * logN)=O(N* logN)

额外空间复杂度：

我们每次执行merge的时候，都需要创建一个temp数组，而这个temp最大是N个数，需要N个空间，所以额外空间复杂度为O(N)