排序算法之冒泡排序

Posted 2021-01-17 wangxiayun

什么是冒泡排序

     冒泡排序是一种交换排序。

     什么是交换排序呢？

      交换排序：两两比较待排序的关键字，并交换不满足次序要求的那对数，直到整个表都满足次序要求为止。

算法思想

    它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。

    这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端，故名。

    假设有一个大小为 N 的无序序列。冒泡排序就是要每趟排序过程中通过两两比较，找到第 i 个小（大）的元素，将其往上排。

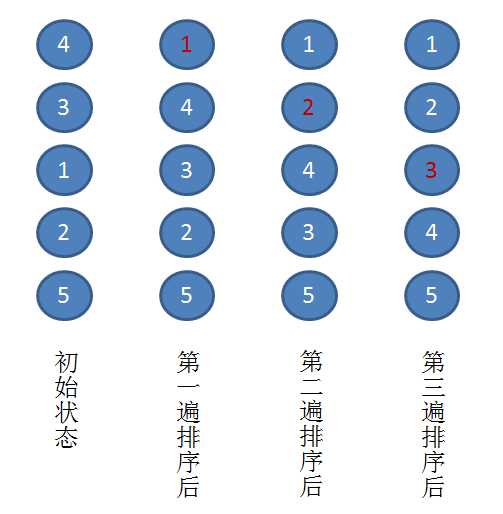
以上图为例，演示一下冒泡排序的实际流程：

假设有一个无序序列  { 4. 3. 1. 2, 5 }

第一趟排序：通过两两比较，找到第一小的数值 1 ，将其放在序列的第一位。

第二趟排序：通过两两比较，找到第二小的数值 2 ，将其放在序列的第二位。

第三趟排序：通过两两比较，找到第三小的数值 3 ，将其放在序列的第三位。

至此，所有元素已经有序，排序结束。 

 

要将以上流程转化为代码，我们需要像机器一样去思考，不然编译器可看不懂。

假设要对一个大小为 N 的无序序列进行升序排序（即从小到大）。 

(1) 每趟排序过程中需要通过比较找到第 i 个小的元素。

所以，我们需要一个外部循环，从数组首端(下标 0) 开始，一直扫描到倒数第二个元素（即下标 N - 2) ，剩下最后一个元素，必然为最大。

(2) 假设是第 i 趟排序，可知，前 i-1 个元素已经有序。现在要找第 i 个元素，只需从数组末端开始，扫描到第 i 个元素，将它们两两比较即可。

所以，需要一个内部循环，从数组末端开始（下标 N - 1），扫描到 (下标 i + 1)。

核心代码

public void bubbleSort(int[] list) {
    int temp = 0; // 用来交换的临时数
 
    // 要遍历的次数
    for (int i = 0; i < list.length - 1; i++) {
        // 从后向前依次的比较相邻两个数的大小，遍历一次后，把数组中第i小的数放在第i个位置上
        for (int j = list.length - 1; j > i; j--) {
            // 比较相邻的元素，如果前面的数大于后面的数，则交换
            if (list[j - 1] > list[j]) {
                temp = list[j - 1];
                list[j - 1] = list[j];
                list[j] = temp;
            }
        }
 
        System.out.format("第 %d 趟：	", i);
        printAll(list);
    }
}

算法分析

 冒泡排序算法的性能

 

排序类别	排序方法	时间复杂度			空间复杂度	稳定性	复杂性
		平均情况	最坏情况	最好情况
交换排序	冒泡排序	O(N2)	O(N2)	O(N)	O(1)	稳定	简单

 

 

时间复杂度

若文件的初始状态是正序的，一趟扫描即可完成排序。所需的关键字比较次数C和记录移动次数M均达到最小值：C_min = N - 1, M_min = 0。所以，冒泡排序最好时间复杂度为O(N)。
若初始文件是反序的，需要进行 N -1 趟排序。每趟排序要进行 N - i 次关键字的比较(1 ≤ i ≤ N - 1)，且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下，比较和移动次数均达到最大值：
C_max = N(N-1)/2 = O(N²)
M_max = 3N(N-1)/2 = O(N²)
冒泡排序的最坏时间复杂度为O(N²)。
因此，冒泡排序的平均时间复杂度为O(N²)。
总结起来，其实就是一句话：当数据越接近正序时，冒泡排序性能越好。

算法稳定性

冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较，交换也发生在这两个元素之间。

所以相同元素的前后顺序并没有改变，所以冒泡排序是一种稳定排序算法。

算法优化

对冒泡排序常见的改进方法是加入标志性变量exchange，用于标志某一趟排序过程中是否有数据交换。

如果进行某一趟排序时并没有进行数据交换，则说明所有数据已经有序，可立即结束排序，避免不必要的比较过程。

// 对 bubbleSort 的优化算法

public void bubbleSort_2(int[] list) {

    int temp = 0; // 用来交换的临时数

    boolean bChange = false; // 交换标志

    // 要遍历的次数

    for (int i = 0; i < list.length - 1; i++) {

        bChange = false;

        // 从后向前依次的比较相邻两个数的大小，遍历一次后，把数组中第i小的数放在第i个位置上

        for (int j = list.length - 1; j > i; j--) {

            // 比较相邻的元素，如果前面的数大于后面的数，则交换

            if (list[j - 1] > list[j]) {

                temp = list[j - 1];

                list[j - 1] = list[j];

                list[j] = temp;

                bChange = true;

            }

        }

        // 如果标志为false，说明本轮遍历没有交换，已经是有序数列，可以结束排序

        if (false == bChange)

            break;
        System.out.format("第 %d 趟：	", i);

        printAll(list);

    }

}

完整参考代码

package notes.javase.algorithm.sort;
 
import java.util.Random;
 
public class BubbleSort {
 
    public void bubbleSort(int[] list) {
        int temp = 0; // 用来交换的临时数
 
        // 要遍历的次数
        for (int i = 0; i < list.length - 1; i++) {
            // 从后向前依次的比较相邻两个数的大小，遍历一次后，把数组中第i小的数放在第i个位置上
            for (int j = list.length - 1; j > i; j--) {
                // 比较相邻的元素，如果前面的数大于后面的数，则交换
                if (list[j - 1] > list[j]) {
                    temp = list[j - 1];
                    list[j - 1] = list[j];
                    list[j] = temp;
                }
            }
 
            System.out.format("第 %d 趟：	", i);
            printAll(list);
        }
    }
 
    // 对 bubbleSort 的优化算法
    public void bubbleSort_2(int[] list) {
        int temp = 0; // 用来交换的临时数
        boolean bChange = false; // 交换标志
 
        // 要遍历的次数
        for (int i = 0; i < list.length - 1; i++) {
            bChange = false;
            // 从后向前依次的比较相邻两个数的大小，遍历一次后，把数组中第i小的数放在第i个位置上
            for (int j = list.length - 1; j > i; j--) {
                // 比较相邻的元素，如果前面的数大于后面的数，则交换
                if (list[j - 1] > list[j]) {
                    temp = list[j - 1];
                    list[j - 1] = list[j];
                    list[j] = temp;
                    bChange = true;
                }
            }
 
            // 如果标志为false，说明本轮遍历没有交换，已经是有序数列，可以结束排序
            if (false == bChange)
                break;
 
            System.out.format("第 %d 趟：	", i);
            printAll(list);
        }
    }
 
    // 打印完整序列
    public void printAll(int[] list) {
        for (int value : list) {
            System.out.print(value + "	");
        }
        System.out.println();
    }
 
    public static void main(String[] args) {
        // 初始化一个随机序列
        final int MAX_SIZE = 10;
        int[] array = new int[MAX_SIZE];
        Random random = new Random();
        for (int i = 0; i < MAX_SIZE; i++) {
            array[i] = random.nextInt(MAX_SIZE);
        }
 
        // 调用冒泡排序方法
        BubbleSort bubble = new BubbleSort();
        System.out.print("排序前:	");
        bubble.printAll(array);
        // bubble.bubbleSort(array);
        bubble.bubbleSort_2(array);
        System.out.print("排序后:	");
        bubble.printAll(array);
    }
}

运行结果

排序前:      2    9    9    7    1    9    0    2    6    8   

第 0 趟：    0    2    9    9    7    1    9    2    6    8   

第 1 趟：    0    1    2    9    9    7    2    9    6    8   

第 2 趟：    0    1    2    2    9    9    7    6    9    8   

第 3 趟：    0    1    2    2    6    9    9    7    8    9   

第 4 趟：    0    1    2    2    6    7    9    9    8    9   

第 5 趟：    0    1    2    2    6    7    8    9    9    9   

排序后:      0    1    2    2    6    7    8    9    9    9