粮食温度预测基于matlab GA优化BP神经网络粮食温度预测研（多输入单输出）（含优化前的对比）含Matlab源码 2404期

Posted 2023-03-07 海神之光

⛄一、遗传算法优化BP神经网络的粮食温度预测

摘 要
针对粮食储存中温度参数的非线性时间序列问题，提出一种基于遗传算法(GA)优化BP神经网络算法的粮食温度预测模型，选取影响粮食温度的10个因素(仓外温度、仓外湿度、仓内顶温度、仓内中心温度、仓内底温度、仓内顶湿度、仓内中心湿度、仓内底湿度、仓内氧气浓度、粮食湿度)作为输入参数，分析后输出粮食温度。经验证，GA-BP模型具有比传统BP神经网络更好的预测精度和实用效果，在粮温预测领域中具有一定的应用前景。

粮食最重要的安全指标之一为粮食的温湿度，其过大会导致粮食的霉变[1]。目前国家各级粮库只能局限于对粮食数据的实时监测和分析，而对于粮食温度信息及其变化趋势只能依靠具有丰富经验的工作人员进行主观的判断[2],因此，如果有一种模型可以对粮食温度的变化进行合理的预测，对粮食安全具有重要的意义。

近年来，运用BP神经网络来预测粮食温度，解决了传统方法解决不了的许多问题，但是也有自身的缺陷，比如预测的准确性有待提高，但加入遗传算法(GA)可以大幅度地提高预测的准确性，达到很好的预测效果[3]。

本文运用遗传算法优化BP神经网络模型，在对数据进行处理后，设置相关的参数和隐含层数，对GA-BP模型进行搭建，提出相应的模型算法，直至训练出最佳的模型。同时，将BP预测模型作为其对比，通过不同模型数据预测的拟合效果进行评价。

1 遗传算法优化BP神经网络
1.1 BP神经网络(back propagation)
BP网络是一种非线性的系统，高度的自适应性是它最为显著的特点。该算法将研究对象的n个样本X=(x1,x2,…,xj,…,xn)作为神经网络的输入层节点，期望结果Y=(y1,y2,…,yj,…,yn)作为相应的输出节点，对权值和阈值进行计算，计算实际结果和预测结果的误差值，见式(1)。适应度函数是衡量误差值是否符合要求的标准，对不满足要求的计算结果，网络将进行误差反向传播，式(2)为隐含层和输出层的修正量，通过反复迭代，若误差达到预期，则模型建立成功。

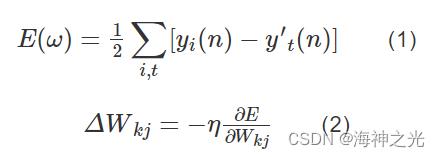
式中：yi (n)为期望结果；y′i(n)为预测结果；η为学习率；E为隐含层输出值；Wkj为输出层该点节点的输出值；ΔWkj为修正量。

1.2 遗传算法(genetic algorithm)
遗传算法的基本思路为一个需要优化的种群，在根据适者生存的基础上，逐代(generation)进化，将进化后具有较好的适应度种群留下并遗传到下一代，在此过程中还需要对其进行交叉和变异的操作，使其产生具有更好适应度的新种群。优化过程如图2所示。

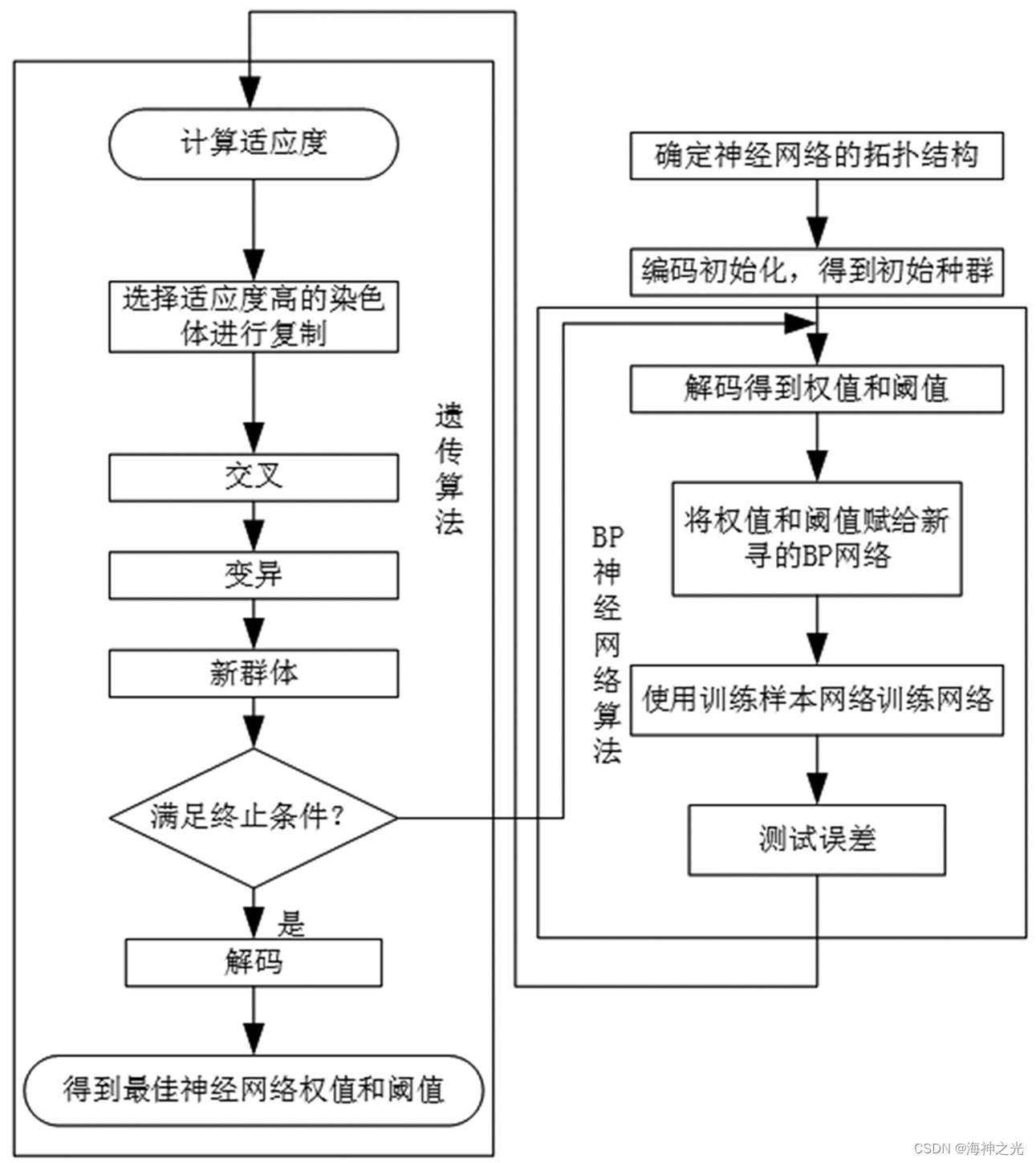
图2 遗传算法优化BP神经网络算法流程示意图

1.2.1 染色体编码
编码规则选用浮点数编码，一方面能够获得更高精度的网络权值和阈值，另一方面还能够获得比之前更广的搜索范围[4],其长度s见式(3)。

s=n1×n2+n2×n3+n2+n3 (3)

式中：n1、n2、n3为输入层、隐含层和输出层神经元的个数。

1.2.2 适应度函数
在训练BP神经网络的过程中，选取网络的输出和期望的输出y¯(k)为训练样本，y(k)作为训练后产生的输出，将训练后的权值和阈值作为选取的权值和阈值，遗传算法的指标作为优化后算法的指标[5],并计算预测值与实际值的误差平方和，见式(4)。

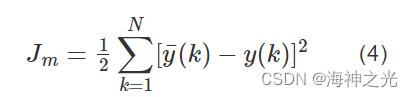
其中：k为输入输出采样数据的对数，N为网络输出节点数，y¯(k)为第k个节点的期望输出值，y(k)为第k个节点的预测输出值。为了避免除零现象的出现，在这里引入一个趋近于零的值ζ,适应度函数见式(5)。

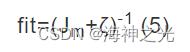
1.2.3 选择
设群体大小为n, fi为适应度，此适应度是就种群中的个体i而言的，则i被选择的概率见式(6)。

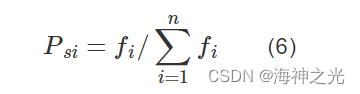
1.2.4 交叉
算数交叉的方法普遍被运用在浮点数交叉的个体当中。假设在个体xtA和xtB之间进行算数交叉，运算后产生的新个体[6]见式(7)。

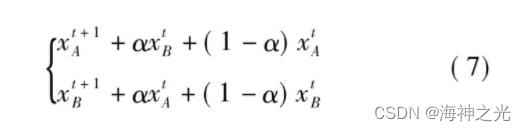
式中：α为区间[0,1]内均匀分布的随机数。

1.2.5 变异
为了防止早熟现象的出现，在一个小范围内的随机数的基础上，使其在小范围概率上发生基因变异，算法的局部搜索能力在这一步也会被加强。此时，假设种群的初始个体的最大值和最小值分别取xmax和xmin,那么变异后的基因[7]见式(8)。

xk=xmin+β(xmin+xmax) (8)

式中：β为区间[0,1]内均匀分布的随机数。

2 粮食温度预测模型的建立
2.1 数据归一化处理
影响粮食温度的因素有许多，不同的因素对于粮食温度变化的影响程度也不尽相同，根据天津市某粮仓2020年9月份的240份水稻数据，选取10个输入指标[8]。为了提高预测精度，在数据采集的过程中将时间段尽量压缩，1 d中每隔3 h进行1次数据采集，将粮食的温度作为模型的输出，训练样本数据如表1所示。

将整个数据分为测试样本和训练样本，前者选取240份数据的前200份，后者取剩余的40份，由于所有收集的数据在数量级上的差异较大，会对网络训练的输出有着直接或者间接的影响，因此，对数据进行归一化处理可以很好地减小其影响。让原本输入的较大数值仍然落到函数梯度较大的位置，这样可以提高模型的收敛速度。假设X=Xi数据归一化为X′=X′i,公式见式(9)。

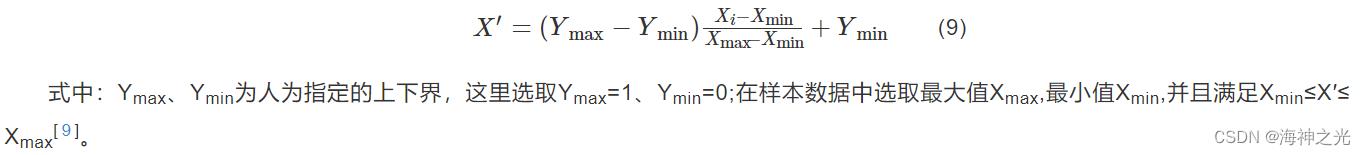
2.2 模型参数的确立
2.2.1 基本参数确定
2.2.1.1 学习速率
学习速率选择过大或者过小都会对模型产生负面影响，学习速率过大，系统会出现不规律的振荡；当学习速率较小时，模型训练的时间相较于之前会大幅的延长。最终学习速率确定为LP.lr=0.01。

2.2.1.2 目标精度
模型训练的精度也与其有着重要的联系，根据文献[10]得出的相应的关系可知，训练时间随着目标精度的提高而增加。试算是目前主要的获取精度的方法，本文的目标精度设为0.005。

2.2.1.3 交叉概率
遗传算法的交叉概率落在0～1之间，本文选择0.15作为交叉概率。

2.2.1.4 变异概率
为保证系统的稳定性，算法的变异概率通常落在0～0.1之间，本文选择0.05作为变异概率。

2.2.2 遗传算法的优化
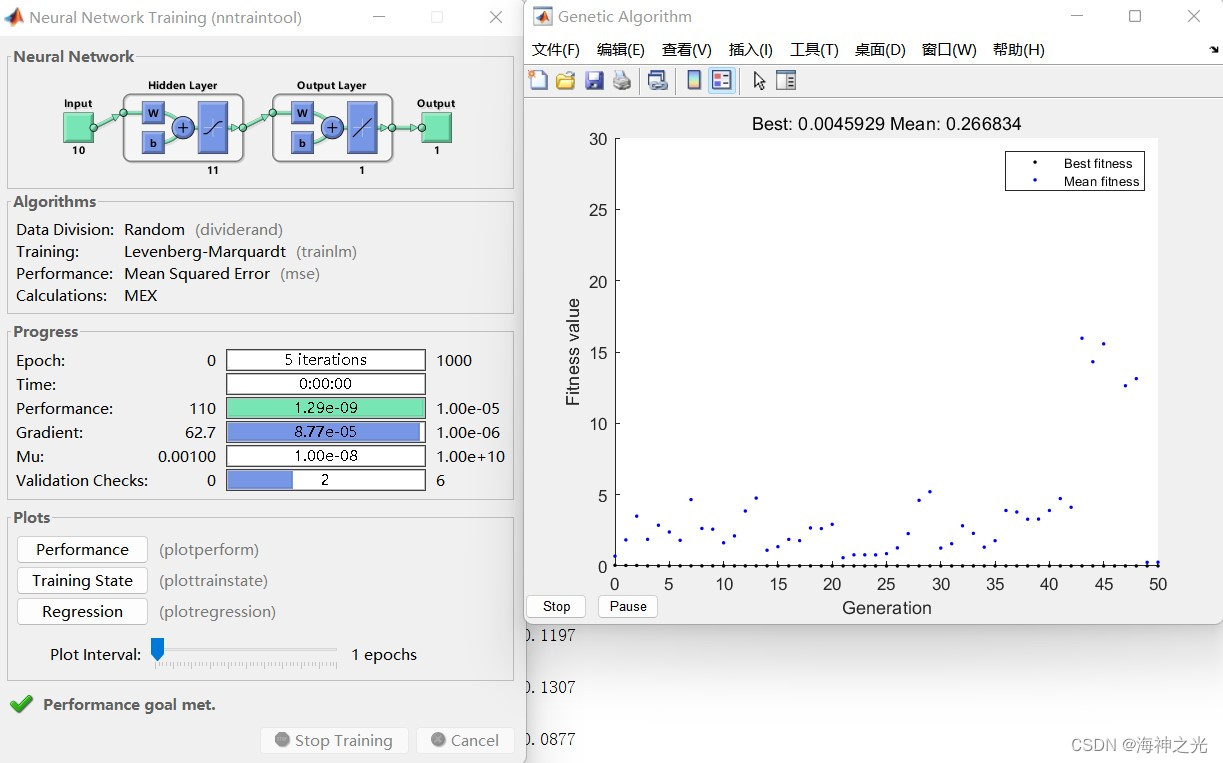
由图3可知：选择代数在靠近50代的位置就已经完全收敛，此时的输出结果同实际的输出结果的真实值的误差越来越小，说明此模型有较好的收敛性，且此时的模型结构也是最合理的。

2.2.3 网络训练
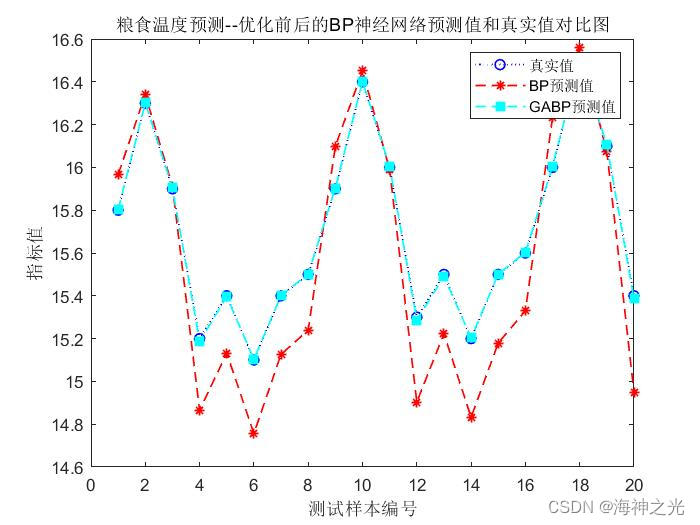
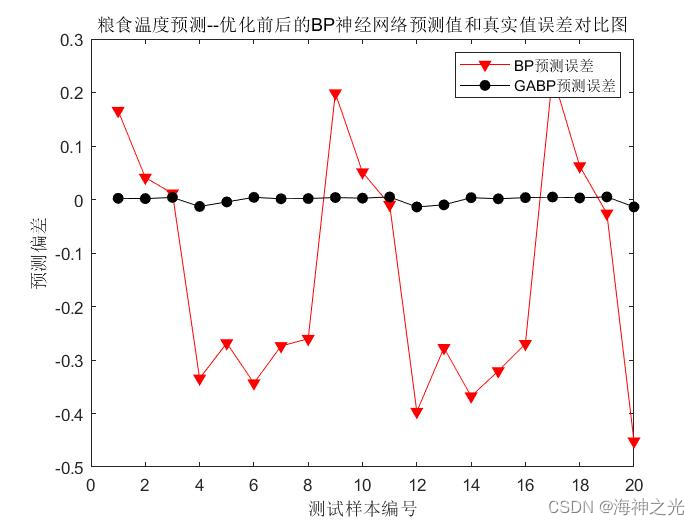
由图4可知：虽然2种模型的预测趋势相对一致，但是也存在着不小的差距，优化后的模型拟合的曲线相较于未优化的曲线更接近于实际曲线。

3 结论
本文提出GA-BP储粮温度预测模型，依据天津市某粮仓的实际水稻数据进行仿真验证，结果显示：在预测精度和实用效果方面GA-BP模型明显优于传统BP神经网络模型，具备较高的优越性。但在今后实际应用中，还需考虑更多现实的问题，比如在更偏南或者偏北方的地域，需细化分类以提高模型的适应度和准确性。

⛄二、部分源代码

%% 初始化
clear
close all
clc
warning off

%% 读取读取
data=xlsread(‘表1神经网络训练样本.xls’,‘Sheet1’,‘B3:L82’); %%使用xlsread函数读取EXCEL中对应范围的数据即可

%输入输出数据
input=data(:,1:end-1); %data的第一列-倒数第二列为特征指标
output=data(:,end); %data的最后面一列为输出的指标值

N=length(output); %全部样本数目
testNum=20; %设定测试样本数目
trainNum=N-testNum; %计算训练样本数目

%% 划分训练集、测试集
input_train = input(1:trainNum,:)‘;
output_train =output(1:trainNum)’;
input_test =input(trainNum+1:trainNum+testNum,:)‘;
output_test =output(trainNum+1:trainNum+testNum)’;

%% 数据归一化
[inputn,inputps]=mapminmax(input_train,0,1);
[outputn,outputps]=mapminmax(output_train);
inputn_test=mapminmax(‘apply’,input_test,inputps);

%% 获取输入层节点、输出层节点个数
inputnum=size(input,2);
outputnum=size(output,2);
disp(‘/’)
disp(‘神经网络结构…’)
disp([‘输入层的节点数为：’,num2str(inputnum)])
disp([‘输出层的节点数为：’,num2str(outputnum)])
disp(’ ')
disp(‘隐含层节点的确定过程…’)

%确定隐含层节点个数
%采用经验公式hiddennum=sqrt(m+n)+a，m为输入层节点个数，n为输出层节点个数，a一般取为1-10之间的整数
MSE=1e+5; %初始化最小误差
for hiddennum=fix(sqrt(inputnum+outputnum))+1:fix(sqrt(inputnum+outputnum))+10

%构建网络
net=newff(inputn,outputn,hiddennum);
% 网络参数
net.trainParam.epochs=1000;         % 训练次数
net.trainParam.lr=0.01;                   % 学习速率
net.trainParam.goal=0.000001;        % 训练目标最小误差
% 网络训练
net=train(net,inputn,outputn);
an0=sim(net,inputn);  %仿真结果
mse0=mse(outputn,an0);  %仿真的均方误差
disp(['隐含层节点数为',num2str(hiddennum),'时，训练集的均方误差为：',num2str(mse0)])

%更新最佳的隐含层节点
if mse0<MSE
    MSE=mse0;
    hiddennum_best=hiddennum;
end

end

⛄三、运行结果

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]郭利进,乔志忠.基于遗传算法优化BP神经网络的粮食温度预测研究[J].粮食与油脂. 2023,36(01)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除