逻辑斯蒂回归

Posted 2021-01-17 sench

逻辑斯蒂回归（logistic regression）是经典的分类方法。虽然名字中包含回归，但它被用来分类。

逻辑斯蒂分布

设 (X) 是随机变量，(X) 服从逻辑斯蒂分布是指 (X) 的概率分布函数 (F(x)) 和概率密度函数 (f(x)) 为：

[F(x) = P(X le x) = frac{1}{1+e^{-(x-mu)/ gamma}}]

[f(x) = F'(x) = frac{e^{-(x-mu)/ gamma}}{gamma(1+e^{-(x-mu)/gamma})^2}]

其中，(mu) 是位置参数，(gamma > 0) 是形状参数。密度函数 (f(x)) 和分布函数 (F(x)) 的图形如下所示：

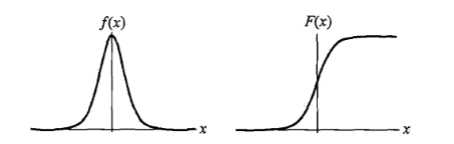
可以看到，分布函数 (F(x)) 是一条 S 型曲线，该曲线在两边增长较缓，而中心增长较快。(mu) 控制着曲线的位置，(F(x)) 关于 ((mu, frac{1}{2})) 中心对称，而 (gamma) 则控制曲线的形状，(gamma) 越小，曲线在中心附近增长的越快。

二项逻辑斯蒂回归模型

二项逻辑斯蒂回归（binomial logistic regression model）是一种分类模型，二项代表该模型被用来进行二类分类。二项逻辑斯蒂回归由条件概率 (P(Y|X)) 表示，其中随机变量 (X) 的取值为实数，随机变量 (Y) 的取值为 0 或 1 。通过训练数据（监督学习）来估计模型的参数，从而确定模型。

二项逻辑斯蒂回归的定义

二项逻辑斯蒂回归是如下的条件概率分布：

[P(Y=1|X) = frac{exp(w cdot x +b)}{1+exp(w cdot x +b)} ag{1}]

[P(Y=0|X) = frac{1}{1+exp(w cdot x + b)} ag{2}]

其中， (x in mathbb{R}^n) 是一个 n 维向量，为输入，(w in mathbb{R}^n) 和 (b in mathbb{R}) 为参数，(w) 被称为权值向量， (b) 被称为偏置，(w cdot x) 为两者的內积。
对于给定的输入实例 (x)， 可以根据(1)(2)两式计算出两个概率 (P(Y=1|X)) 和 (P(Y=0|X))，比较两个概率的大小，将实例 (x) 分到概率较大的那一类。
有时，为了方便，可以对 (w) 和 (x) 进行扩充，扩充后 (w= (w^1,w^2,...,w^n,b))，(x=(x^1,x^2,...,x^n,1))，这样(w cdot x) 就相当于扩充前的 (w cdot x+ b)，所以式（1）（2）可以改写为：

[P(Y=1|X) = frac{exp(w cdot x)}{1+exp(w cdot x)} ag{3}]

[P(Y=0|X) = frac{1}{1+exp(w cdot x )} ag{4}]

可以看到，当线性函数 (w cdot x) 的值越接近于正无穷，概率值就越接近于 1 ；线性函数值越接近于负无穷，概率就越接近于 0 ，这与前面 (F(x)) 的图像一致，所以该模型就是逻辑斯蒂回归模型。

模型的参数估计

给定训练集 (T={(x_1,y_1),(x_2,y_2),...,(x_n,y_n)})，其中(x_i in mathbb{R}^n)，(y_i in {0,1})，可以使用极大似然估计法来估计模型的参数 (w)，从而得到逻辑斯蒂回归模型。步骤如下：
假设：

[P(Y=1|x)=pi(x), quad P(Y=0|x)=1-pi(x)]

似然函数为：

[prod_{i=1}^N[pi(x_i)]^{y_i}[1-pi(x_i)]^{1-y_i}]

对数似然函数为：

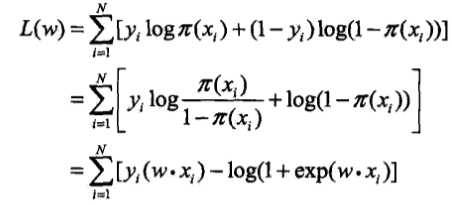
对 (L(w)) 求极大值，就得到了 (w) 的估计值。
这样，问题就变成了求以对数似然函数为目标函数的最优化问题，逻辑斯蒂回归学习通常使用梯度下降法和拟牛顿法。
假设估计的参数值为 (hat w)，则学到的二项逻辑斯蒂回归模型为：

[P(Y=1|X) = frac{exp(hat w cdot x)}{1+exp(hat w cdot x)} ]

[P(Y=0|X) = frac{1}{1+exp(hat w cdot x )}]

多项逻辑斯蒂回归

可以将二项逻辑斯蒂回归推广到多项逻辑斯蒂回归。假设随机变量 (Y) 的取值集合为 ({0, 1, ..., K})，则多项逻辑斯蒂回归的模型就是：

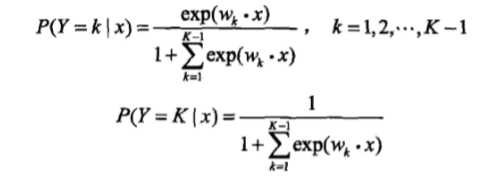
其中，(x in mathbb{R}^{n+1})，(w_k in mathbb{R}^{n+1})。
同样可以使用极大似然估计来估计模型中的参数。

逻辑斯蒂回归的实现

这里使用python库scikit-learn来实现逻辑斯蒂回归，使用的方法为sklearn.linear_model.SGDClassifier，该方法使用梯度下降来实现逻辑斯蒂回归，函数的使用方法和参数含义可以参考文档。
训练数据如下：

1,0,0,1,0
1,0,0,2,0
1,1,0,2,1
1,1,1,1,1
1,0,0,1,0
2,0,0,1,0
2,1,1,2,0
2,1,1,2,1
2,0,1,3,1
2,0,1,3,1
3,0,1,3,1
3,0,1,2,1
3,1,0,2,1
3,1,0,3,1
3,0,0,1,0

数据来自贷款信息，每一行代表一个实例（贷款人）。数据共分为5列，前4列为属性值，分别是年龄（1青年，2中年，3老年）、是否有房子（0没房子，1有房子）、是否有工作（0没工作，1有工作）和信用值（1,2,3分别是信用一般，好，非常好），最后一列为类别（0代表没有贷款资格，1代表有贷款资格）。目标是训练出一个逻辑斯蒂回归模型，输入新的实例，判断该实例是否有贷款资格。将上面的数据保存到data.txt，代码如下：

import numpy as np
import pandas as pd
from sklearn import linear_model

df = pd.read_csv("D:\\data.txt", header=None)
# 属性值
xdata = df.loc[:,:3]
#类别
ydata = df.loc[:,4]

clf = linear_model.SGDClassifier(loss="log", max_iter=1000)  #log代表logistic
clf.fit(xdata, ydata)

# 青年人、没工作、有房子、信用好
clf.predict(np.array([1,0,1,1]).reshape(1,-1))

输出：

array([0], dtype=int64)

0代表该申请人没有贷款资格。
除了这个方法外，还可以使用sklearn.linear_model.LogisticRegression以及sklearn.linear_model.LogisticRegressionCV来实现逻辑斯蒂回归。

总结

逻辑斯蒂回归模型是一种经典的分类模型，它根据条件概率的取值来对实例进行分类。可以使用极大似然估计来估计模型中的参数 (w) 。

参考

1、李航《统计学习方法》