P1074 靶形数独

Posted 2021-01-17 edsheeran

P1074 靶形数独 

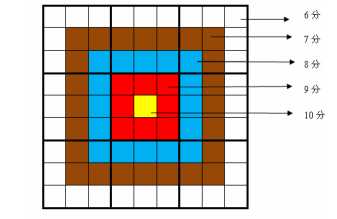
比赛的要求是：每个人必须完成一个给定的数独（每个给定数独可能有不同的填法），而且要争取更高的总分数。而这个总分数即每个方格上的分值和完成这个数独时填在相应格上的数字的乘积的总和

 

输入输出格式

输入格式：

 

一共 99 行。每行99个整数（每个数都在 0-9的范围内），表示一个尚未填满的数独方格，未填的空格用“00”表示。每两个数字之间用一个空格隔开。

 

输出格式：

 

输出共 11 行。输出可以得到的靶形数独的最高分数。如果这个数独无解，则输出整数-1?1。

 

输入输出样例

输入样例#1： 复制

7 0 0 9 0 0 0 0 1 
1 0 0 0 0 5 9 0 0 
0 0 0 2 0 0 0 8 0 
0 0 5 0 2 0 0 0 3 
0 0 0 0 0 0 6 4 8 
4 1 3 0 0 0 0 0 0 
0 0 7 0 0 2 0 9 0 
2 0 1 0 6 0 8 0 4 
0 8 0 5 0 4 0 1 2

输出样例#1： 复制

2829

输入样例#2： 复制

0 0 0 7 0 2 4 5 3 
9 0 0 0 0 8 0 0 0 
7 4 0 0 0 5 0 1 0 
1 9 5 0 8 0 0 0 0 
0 7 0 0 0 0 0 2 5 
0 3 0 5 7 9 1 0 8 
0 0 0 6 0 1 0 0 0 
0 6 0 9 0 0 0 0 1 
0 0 0 0 0 0 0 0 6

输出样例#2： 复制

2852

说明

【数据范围】

40%的数据，数独中非 00 数的个数不少于3030。

80%的数据，数独中非 00 数的个数不少于2626。

100%的数据，数独中非00数的个数不少于2424。

NOIP 2009 提高组 第四题

 

题解：迭代搜素

如果剩下的格子我全部填九得到的分都没有当前的分高，停止搜索

按照数独的思想，要先从格子剩的少的地方填

对于第一个剪枝我每次都重新搜了一遍，后来发现可以预先处理，每次减掉一个格子的贡献(自己太也SB了)

还可以用位运算更快

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int M = 3e5 + 5, P = 3e5;
int a[12][12], tot[12], z[12];
int banx[12], bany[12], ban[12], bin[12];

int id[12][12] = {
{0},
{0, 1, 1, 1, 2, 2, 2, 3, 3, 3},
{0, 1, 1, 1, 2, 2, 2, 3, 3, 3},
{0, 1, 1, 1, 2, 2, 2, 3, 3, 3},
{0, 4, 4, 4, 5, 5, 5, 6, 6, 6},
{0, 4, 4, 4, 5, 5, 5, 6, 6, 6},
{0, 4, 4, 4, 5, 5, 5, 6, 6, 6},
{0, 7, 7, 7, 8, 8, 8, 9, 9, 9},
{0, 7, 7, 7, 8, 8, 8, 9, 9, 9},
{0, 7, 7, 7, 8, 8, 8, 9, 9, 9}
};
int sc[12][12] = {
{0},
{0, 6, 6, 6, 6, 6, 6, 6, 6, 6},
{0, 6, 7, 7, 7, 7, 7, 7, 7, 6},
{0, 6, 7, 8, 8, 8, 8, 8, 7, 6},
{0, 6, 7, 8, 9, 9, 9, 8, 7, 6},
{0, 6, 7, 8, 9, 10,9, 8, 7, 6},
{0, 6, 7, 8, 9, 9, 9, 8, 7, 6},
{0, 6, 7, 8, 8, 8, 8, 8, 7, 6},
{0, 6, 7, 7, 7, 7, 7, 7, 7, 6},
{0, 6, 6, 6, 6, 6, 6, 6, 6, 6}
};

int ans = -1, res;

void dfs(int dep, int sum, int y){
    if(dep == 10){
        ans = max(ans, sum); return ;
    }
    if(ans != -1 && sum + res <= ans) return ;
    int x = z[dep], tmp = 0;
    while(a[x][y])y++;
    if(y == 10) dfs(dep+1, sum, 1);
    else {
        for(int i = 9; i; i--)
            if(!(banx[x]&bin[i]) && !(bany[y]&bin[i]) && !(ban[id[x][y]]&bin[i])){
                banx[x]^=bin[i];bany[y]^=bin[i];ban[id[x][y]]^=bin[i];
                res -= 9 * sc[x][y], a[x][y] = i; 
                int to = y + 1; while(a[x][to])to++;
                if(to == 10)dfs(dep+1, sum + i*sc[x][y], 1);
                else dfs(dep, sum + i*sc[x][y], to);
                res += 9 * sc[x][y], a[x][y] = 0;
                banx[x]^=bin[i];bany[y]^=bin[i];ban[id[x][y]]^=bin[i];
            }    
    }    
}
bool cmp(int a, int b){return tot[a] > tot[b];}

int main(){
//    freopen("hehe.out","w",stdout);
    int now = 0, fg = 0;
    bin[1] = 1;
    for(int i = 2; i <= 9; i++) bin[i] = bin[i-1]<<1;
    for(int i = 1; i <= 9; i++)
        for(int j = 1; j <= 9; j++){
            scanf("%d", &a[i][j]);
            if(a[i][j]){
                if(banx[i]&bin[a[i][j]]) fg = 1;
                if(bany[j]&bin[a[i][j]]) fg = 1;
                if(ban[id[i][j]]&bin[a[i][j]]) fg = 1;
                tot[i]++;
                banx[i] |= bin[a[i][j]];
                bany[j] |= bin[a[i][j]];
                ban[id[i][j]] |= bin[a[i][j]];
                now += a[i][j] * sc[i][j];
            } else res += 9 * sc[i][j];
        }
    for(int i = 1; i <= 9; i++)z[i] = i;
    sort(z + 1, z + 1 + 9, cmp);
    if(fg)return !printf("-1
");
    int xx = 1, yy = 1;
    while(tot[z[xx]] == 9)xx++;
    while(a[z[xx]][yy])yy++;
    dfs(xx, 0, yy);
    if(ans == -1) printf("-1");
    else printf("%d
",ans + now);
}

View Code