noip2017

Posted 2021-01-17 bzmd

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了noip2017相关的知识，希望对你有一定的参考价值。

描述

小凯手中有两种面值的金币，两种面值均为正整数且彼此互素。每种金币小凯都有无数个。在不找零的情况下，仅凭这两种金币，有些物品他是无法准确支付的。现在小凯想知道在无法准确支付的物品中，最贵的价值是多少金币？注意：输入数据保证存在小凯无法准确支付的商品

格式

输入格式

输入数据仅一行，包含两个正整数

输出格式

输出文件仅一行，一个正整数

样例1

样例输入1

3 7

样例输出1

提示

小凯手中有面值为

12 = 3 * 4 + 7 * 0

13 = 3 * 2 + 7 * 1

14 = 3 * 0 + 7 * 2

15 = 3 * 5 + 7 * 0

限制

对于 $30\\%30% 的数据： 1 le a, b le 501≤a,b≤50。$

对于 $60\\%60% 的数据： 1 le a, b le 100001≤a,b≤10000。$

对于 $100\\%100% 的数据：1 le a, b le 10000000001≤a,b≤1000000000。$

首先不妨设a<b，对于数k来说k%b的余数在0~b-1间,设c=k%b,设k=z*b+c;(z为非负整数）当z==0时，能够凑出的k对应的c有0,a而由于此时a是合法的，也就意味着z>=0，c=a必然合法

然后继续c=a*2%b,这是会把这以后对应的z*b+c也成为合法，而由于gcd(a,b)=1,所以1*a%b,2*a%b...(b-1)*a%b的结果全部不同（证明在下面），根据抽屉原理，此时所有余数都被覆盖也就意味着更大的值也会被覆盖

而最后一个余数对应的是(b-1)*a在上一轮对应此余数还没有覆盖所以是(b-1)*a-b;

反证法证明上述结论，假设有i*a%b==j*a%b 其中i!=j,0<i,j<b;

所以就知道了i*a=I*b+t,j*a=J*b+t;

(i-j)*a=(I-J)*b;

gcd(a,b)=1,i-j<b;

所以上式显然不成立

#include<cstdio>
int main(){
    long long a,b;
    scanf("%lld%lld",&a,&b);
    printf("%lld",a*b-a-b);
}

描述

小明正在学习一种新的编程语言

A++语言的循环结构如下：

F i x y
循环体
E

其中 "F i x y" 表示新建变量（

"E" 表示循环体结束。循环体结束时，这个循环体新建的变量也被销毁。

注：本题中为了书写方便，在描述复杂度时，使用大写英文字母 "O" 表示通常意义下 "Θ" 的概念。

格式

输入格式

输入文件第一行一个正整数

接下来每个程序的第一行包含一个正整数 $表示常数复杂度，"O(n^w)" 表示复杂度为n^wnw，其中ww是一个小于100100的正整数（输入中不包含引号），输入保证复杂度只有 "O(1)" 和 "O(n^w)"两种类型。$

接下来

程序行若以 "F" 开头，表示进入一个循环，之后有空格分离的三个字符（串）

输出格式

输出文件共

注意：即使在程序不会执行的循环体中出现了语法错误也会编译错误，要输出 "ERR"。

样例1

样例输入1

8
2 O(1)
F i 1 1
E
2 O(n^1)
F x 1 n
E
1 O(1)
F x 1 n
4 O(n^2)
F x 5 n
F y 10 n
E
E
4 O(n^2)
F x 9 n
E
F y 2 n
E
4 O(n^1)
F x 9 n
F y n 4
E
E
4 O(1)
F y n 4
F x 9 n
E
E
4 O(n^2)
F x 1 n
F x 1 10
E
E

样例输出1

Yes
Yes
ERR
Yes
No
Yes
Yes
ERR

限制

对于 $30\\%30% 的数据：不存在语法错误，数据保证小明给出的每个程序的前 L/2L/2 行一定为以 F 开头的语句，第 L/2+1L/2+1 行至第 LL 行一定为以 EE 开头的语句，Lle 10L≤10，若 xx、yy 均为整数，xx 一定小于 yy，且只有 yy 有可能为 nn。$

对于 $50\\%50% 的数据：不存在语法错误，Lle 100L≤100，且若 xx、yy 均为整数，xx 一定小于 yy，且只有 yy 有可能为 nn。$

对于 $70\\%70% 的数据：不存在语法错误，Lle 100L≤100。$

对于 $100\\%100% 的数据：Lle 100L≤100。$

#include<cstdio>
#include<iostream>
#include<cstring>
#include<string>
using namespace std;
char s[10],stc[105];
bool sf[150];
int st[105],lsd[105];
int zh(char *t){
    int l=strlen(t),re=0;
    for(int i=0;i<l;++i) 
        re=re*10+t[i]-‘0‘;
    return re; 
}
int main(){
    freopen("g.in","r",stdin);
    int t;
    scanf("%d",&t);
    while(t--){
        int n,to=0,pd=0,ans=0;
        char s[10];
        for(int i=0;i<100;++i) st[i]=-1;
        memset(sf,0,sizeof(sf));
        scanf("%d%s",&n,s);
        for(int i=1;i<=n;++i){
            char p,c,x[5],y[5];
            scanf("
%c",&p);
            if(p==‘F‘){
                scanf(" %c %s %s",&c,x,y);
                if(sf[c]) pd=1;
                sf[stc[++to]=c]=1;
                if(x[0]==‘n‘&&y[0]==‘n‘) lsd[to]=1;
                else if(y[0]==‘n‘) lsd[to]=2;
                else if(x[0]!=‘n‘) lsd[to]=zh(y)>=zh(x);
                else lsd[to]=0;
                //if(t==5) printf("F %c %s %s
%d %d
",c,x,y,lsd[to],to);
            }
            else{
                if(!to) pd=1;
                if(st[to+1]!=-1&&lsd[to]&&st[to+1]) lsd[to]+=st[to+1]-1;
                st[to]=max(st[to],lsd[to]);
                st[to+1]=-1;
                //if(t==5) printf("E
%d %d
",st[to],to);
                sf[stc[to--]]=0;
            }
        }
        if(to||pd){
            printf("ERR
");
            continue;
        }
        if(s[2]==‘1‘) ans=st[1]<2;
        else{
            s[strlen(s)-1]=0;
            ans=zh(s+4)+1==st[1];
        }
        ans?printf("Yes
"):printf("No
");
    }
    return 0;
}

描述

策策同学特别喜欢逛公园。公园可以看成一张

策策喜欢新鲜的事物，他不希望有两天逛公园的路线完全一样，同时策策还是一个特别热爱学习的好孩子，他不希望每天在逛公园这件事上花费太多的时间。如果

为避免输出过大，答案对

格式

输入格式

第一行包含一个整数

第一行包含四个整数

接下来 $MM行，每行三个整数a_iai?, b_ibi?, c_ici?，代表编号为a_iai?, b_ibi?的点之间有一条权值为 c_ici?的有向边，每两个整数之间用一个空格隔开。$

输出格式

输出文件包含

样例1

样例输入1

样例输出1

3
-1

限制

技术分享图片

30%的数据：https://www.cnblogs.com/bzmd/p/9896449.html 对于K==0的情况，最短路计数问题

下面是30分的代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N=1e5+5;
struct X{
    int v,f,n,q;
}x[N<<1];
queue<int>q;
int d[N],cnt[N],vis[N];
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        int n,m,u,k,p;
        scanf("%d%d%d%d",&n,&m,&k,&p);
        memset(x,0,sizeof(x));
        memset(cnt,0,sizeof(cnt));
        for(int i=1;i<=m;++i)
        {
            scanf("%d%d%d",&u,&x[i].v,&x[i].q);
            x[i].n=x[u].f;
            x[u].f=i;
        }
        memset(d,0x3f,sizeof(d));
        q.push(cnt[1]=1);
        d[1]=0;vis[n]=vis[1]=1;
        for(;q.size();q.pop()){
            u=q.front();
            for(int i=x[u].f;i;i=x[i].n){
                if(d[u]+x[i].q==d[x[i].v]) cnt[x[i].v]+=cnt[u],cnt[x[i].v]%=p;
                else if(d[u]+x[i].q<d[x[i].v]){
                    d[x[i].v]=d[u]+x[i].q;
                    cnt[x[i].v]=cnt[u];
                }
                if(cnt[x[i].v]&&!vis[x[i].v]) vis[x[i].v]=1,q.push(x[i].v);
            }
            vis[u]=0;cnt[u]=0;
        }
        printf("%d
",cnt[n]);
    }
    return 0;
}

70%的数据没有0边

d[u]表示1到u的最短路

设f[i][j]表示到从1到i路径长度为d[u]+j的数量

u到v有一条边长度为q

方程f[v][j+q-(d[v]-d[u])]+=f[u][j];

记得dp的顺序要保证点i对应d[i]从小到大

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N=1e5+5;
struct X{
    int v,f,n,q;
}x[N<<1];
queue<int>q;
int d[N],vis[N],f[N][55],k,p,wc[N];
bool cmp(const int &a,const int &b){
    return d[a]<d[b];
}
int main(){
    int tt;
    scanf("%d",&tt);
    while(tt--){
        int n,m,u,ans=0;
        scanf("%d%d%d%d",&n,&m,&k,&p);
        memset(x,0,sizeof(x));
        memset(f,0,sizeof(f));
        for(int i=1;i<=m;++i)
        {
            scanf("%d%d%d",&u,&x[i].v,&x[i].q);
            x[i].n=x[u].f;
            x[u].f=i;
        }
        memset(d,0x3f,sizeof(d));
        q.push(vis[1]=1);
        d[1]=0;
        for(;q.size();q.pop()){
            u=q.front();
            for(int i=x[u].f;i;i=x[i].n)
                if(d[u]+x[i].q<d[x[i].v]){
                    d[x[i].v]=d[u]+x[i].q;
                    if(!vis[x[i].v]) vis[x[i].v]=1,q.push(x[i].v);
                }
            vis[u]=0;
        }
        for(int i=1;i<=n;++i) wc[i]=i;
        sort(wc+1,wc+n+1,cmp);
        f[1][0]=1;
        for(int j=0;j<=k;++j){
            for(int l=1;l<=n;++l){
                u=wc[l];
                for(int i=x[u].f;i;i=x[i].n){
                    int t=j+x[i].q-d[x[i].v]+d[u];
                    if(t<=k) f[x[i].v][t]+=f[u][j],f[x[i].v][t]%=p;
                }
            }
        }
        for(int i=0;i<=k;++i) ans=(ans+f[n][i])%p;
        printf("%d
",ans);
    }
    return 0;
}

100%

最后剩下的问题就是如何处理0边了

当有0边时转移的顺序不能直接看d[i]，因为0边连接的几个点d相同。

我们考虑把所有构成最短路的边挑出来（必然有所有0边）这些边满足d[u]+q=d[v]

然后进行拓扑排序就可以求出来了

如果有0环输出-1直接在这里判断

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N=1e5+5;
struct X{
    int v,f,n,q;
}x[N<<1];
queue<int>q;
int d[N],vis[N],f[N][55],k,p,wc[N],rd[N];
int main(){
    int tt;
    scanf("%d",&tt);
    while(tt--){
        int n,m,u,ans=0,s=0;
        scanf("%d%d%d%d",&n,&m,&k,&p);
        memset(x,0,sizeof(x));
        memset(f,0,sizeof(f));
        memset(rd,0,sizeof(rd));
        for(int i=1;i<=m;++i)
        {
            scanf("%d%d%d",&u,&x[i].v,&x[i].q);
            x[i].n=x[u].f;
            x[u].f=i;
        }
        memset(d,0x3f,sizeof(d));
        q.push(vis[1]=1);
        d[1]=0;
        for(;q.size();q.pop()){
            u=q.front();
            for(int i=x[u].f;i;i=x[i].n)
                if(d[u]+x[i].q<d[x[i].v]){
                    d[x[i].v]=d[u]+x[i].q;
                    if(!vis[x[i].v]) vis[x[i].v]=1,q.push(x[i].v);
                }
            vis[u]=0;
        }
        for(int j=1;j<=n;++j)
            for(int i=x[j].f;i;i=x[i].n)
                if(d[j]+x[i].q==d[x[i].v]) rd[x[i].v]++;
        for(int i=1;i<=n;++i)
            if(!rd[i]) wc[++s]=i;
        for(int j=1;j<=s;++j){
            u=wc[j];
            for(int i=x[u].f;i;i=x[i].n)
                if(d[u]+x[i].q==d[x[i].v]){
                    rd[x[i].v]--;
                    if(!rd[x[i].v]) wc[++s]=x[i].v;
                }
        }
        if(s<n){
            printf("-1
");
            continue;
        } 
        f[1][0]=1;
        for(int j=0;j<=k;++j){
            for(int l=1;l<=s;++l){
                u=wc[l];
                for(int i=x[u].f;i;i=x[i].n){
                    int v=x[i].v;
                    int t=j+x[i].q-d[v]+d[u];
                    if(t<=k) f[v][t]+=f[u][j],f[v][t]%=p;
                }
            }
        }
        for(int i=0;i<=k;++i) ans=(ans+f[n][i])%p;
        printf("%d
",ans);
    }
    return 0;
}

奶酪

描述

现有一块大奶酪，它的高度为

现在，奶酪的下表面有一只小老鼠 Jerry，它知道奶酪中所有空洞的球心所在的坐标。如果两个空洞相切或是相交，则 Jerry 可以从其中一个空洞跑到另外一个空洞，特别地，如果一个空洞与下表面相切或是相交， Jerry 则可以从奶酪的下表面跑进空洞；如果一个空洞与上表面相切或是相交， Jerry 则可以从空洞跑到奶酪上表面。

位于奶酪下表面的 Jerry 想知道，在不破坏奶酪的情况下，能否利用已有的空洞跑到奶酪的上表面去？

空间内两点 $P_1(x_1,y_1,z_1)P1?(x1?,y1?,z1?)，P_2(x_2,y_2,z_2)P2?(x2?,y2?,z2?) 的距离公式如下：$

$dist(P_1,P_2)=sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}dist(P1?,P2?)=√(x1??x2?)2+(y1??y2?)2+(z1??z2?)2?。$

格式

输入格式

输入包含多组数据。

输入的第一行，包含一个正整数

第一行包含三个整数

接下来的

输出格式

输出包含

样例1

样例输入1

样例输出1

Yes
No
Yes

限制

对于 $20\\%20% 的数据，n=1n=1，1le h,rle 10,0001≤h,r≤10,000，坐标的绝对值不超过 10,00010,000。$

对于 $40\\%40% 的数据，1le nle 81≤n≤8，1le h,rle 10,0001≤h,r≤10,000，坐标的绝对值不超过 10,00010,000。$

对于 $80\\%80% 的数据，1le nle 1,0001≤n≤1,000，1le h,rle 10,0001≤h,r≤10,000，坐标的绝对值不超过 10,00010,000。$

对于 $100\\%100% 的数据，1le nle 1,0001≤n≤1,000，1le h,rle 1,000,000,0001≤h,r≤1,000,000,000，Tle 20T≤20，坐标的绝对值不超过 1,000,000,0001,000,000,000。$

裸的bfs，只是注意要用sqrt的话浮点数比对会有误差。

#include<cstdio>
#include<cstring>
typedef long long ll;
const int N=1005;
struct X{
    int v,f,n;
}x[N*N];
int s,vis[N],q[N];
struct A{
    ll x,y,z;
}a[N];
void add(int u,int v){
    x[++s].n=x[u].f;
    x[x[u].f=s].v=v;
}
ll f(ll t){
    return t*t;
}
ll jd(ll t){
    return t>0?t:-t;
}
int main(){
    freopen("h.in","r",stdin);
    int t;
    scanf("%d",&t);
    while(t--){
        s=0;
        memset(x,0,sizeof(x));
        memset(vis,0,sizeof(vis));
        int n,t=0,w=0;
        ll h,r;
        scanf("%d%lld%lld",&n,&h,&r);
        for(int i=1;i<=n;++i) scanf("%lld%lld%lld",&a[i].x,&a[i].y,&a[i].z);
        for(int i=1;i<=n;++i)
            for(int j=i+1;j<=n;++j)
                if(f(a[i].x-a[j].x)+f(a[i].y-a[j].y)+f(a[i].z-a[j].z)<=f(r<<1)) add(i,j),add(j,i);
        for(int i=1;i<=n;++i){
            if(jd(a[i].z)<=r) q[w++]=i,vis[i]=1;
            if(jd(h-a[i].z)<=r) add(i,n+1);
        }
        for(;t<w;++t)
            for(int i=x[q[t]].f;i;i=x[i].n)
                if(!vis[x[i].v]){
                    vis[x[i].v]=1;
                    q[w++]=x[i].v;
                }
        vis[n+1]?printf("Yes
"):printf("No
");
    }
    return 0;
}

描述

参与考古挖掘的小明得到了一份藏宝图，藏宝图上标出了

小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是，每个宝藏屋距离地面都很远，也就是说，从地面打通一条到某个宝藏屋的道路是很困难的，而开发宝藏屋之间的道路则相对容易很多。

小明的决心感动了考古挖掘的赞助商，赞助商决定免费赞助他打通一条从地面到某个宝藏屋的通道，通往哪个宝藏屋则由小明来决定。

在此基础上，小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以任意通行不消耗代价。每开凿出一条新道路，小明就会与考古队一起挖掘出由该条道路所能到达的宝藏屋的宝藏。另外，小明不想开发无用道路，即两个已经被挖掘过的宝藏屋之间的道路无需再开发。

新开发一条道路的代价是：这条道路的长度

请你编写程序为小明选定由赞助商打通的宝藏屋和之后的开凿的道路，使得工程总代价最小，并输出这个最小值。

格式

输入格式

第一行两个用空格分离的正整数

接下来

输出格式

输出共一行，一个正整数，表示最小的总代价。

样例1

样例输入1

样例输出1

样例2

样例输入2

样例输出2

限制

对于 $20\\%20% 的数据，保证输入是一棵树，1le nle 81≤n≤8，vle 5000v≤5000 且所有的 vv 都相等。$

对于 $40\\%40% 的数据，1le nle 81≤n≤8，0le mle 10000≤m≤1000，vle 5000v≤5000 且所有的 vv 都相等。$

对于 $70\\%70% 的数据，1le nle 81≤n≤8，0le mle 10000≤m≤1000，vle 5000v≤5000。$

对于 $100\\%100% 的数据，1le nle 121≤n≤12，0le mle 10000≤m≤1000，vle 500000v≤500000。$

并且要注意n=1的情况。

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int M=1<<12,D=1061109567,N=13;
int d[N][N],f[M],q[N],sl[M][N];
int main(){
    freopen("h.in","r",stdin); 
    int n,m,ans=D,anss=0;
    scanf("%d%d",&n,&m);
    if(!m) ans=0;
    memset(d,0x3f,sizeof(d));
    while(m--){
        int u,v,q;
        scanf("%d%d%d",&u,&v,&q);
        d[v][u]=d[u][v]=min(d[u][v],q);
    }
    for(int i=1;i<=n;++i){
        int mx=0;
        memset(f,0x3f,sizeof(f));
        memset(sl,0,sizeof(sl));
        f[1<<i-1]=0;sl[1<<i-1][i]=1;
        for(int j=(1<<i-1)+1;j<1<<n;++j){
            int s=0,jl=-1,jlk,jll;
            for(int k=0;k<n;++k)
                if(j&(1<<k)) q[++s]=k+1;
            for(int k=1;k<=s;++k)
                for(int l=1;l<=s;++l)
                    if(k!=l&&d[q[k]][q[l]]<D){
                        int t=j&(~(1<<q[l]-1));
                        if(f[t]+d[q[k]][q[l]]*sl[t][q[k]]<f[j]){
                            f[j]=f[t]+d[q[k]][q[l]]*sl[t][q[k]];
                            jl=t,jlk=k,jll=l;
                        }
                    }
            if(jl!=-1){
                for(int k=1;k<=n;++k) sl[j][k]=sl[jl][k];
                sl[j][q[jll]]=sl[j][q[jlk]]+1;
                mx=j;
            }
        } 
        ans=min(ans,f[mx]);
    }
    printf("%d",ans);
    return 0;
}

描述

策策同学特别喜欢逛公园。公园可以看成一张

为避免输出过大，答案对

格式

输入格式

第一行包含一个整数

第一行包含四个整数

接下来 $MM行，每行三个整数a_iai?, b_ibi?, c_ici?，代表编号为a_iai?, b_ibi?的点之间有一条权值为 c_ici?的有向边，每两个整数之间用一个空格隔开。$

输出格式

输出文件包含

样例1

样例输入1

样例输出1

3
-1

限制

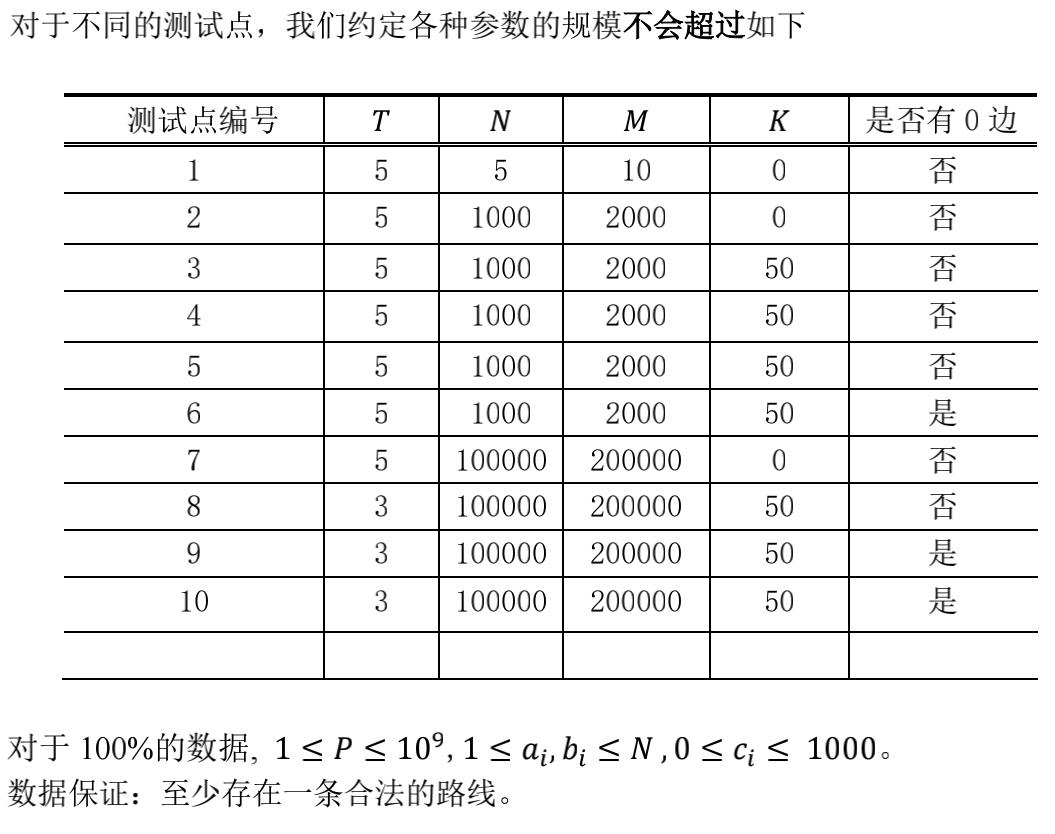
技术分享图片

描述

Sylvia 是一个热爱学习的女孩子。

前段时间，Sylvia 参加了学校的军训。众所周知，军训的时候需要站方阵。Sylvia 所在的方阵中有

为了便于管理，教官在训练开始时，按照从前到后，从左到右的顺序给方阵中的学生从

然而在练习方阵的时候，经常会有学生因为各种各样的事情需要离队。在一天中，一共发生了

在有学生离队后，队伍中出现了一个空位。为了队伍的整齐，教官会依次下达这样的两条指令：

1：向左看齐。这时第一列保持不动，所有学生向左填补空缺。不难发现在这条指令之后，空位在第

2：向前看齐。这时第一行保持不动，所有学生向前填补空缺。不难发现在这条指令之后，空位在第

教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后，下一个学生才能离队。因此在每一个离队的学生要归队时，队伍中有且仅有第

因为站方阵真的很无聊，所以 Sylvia 想要计算每一次离队事件中，离队的同学的编号是多少。

注意：每一个同学的编号不会随着离队事件的发生而改变，在发生离队事件后方阵中同学的编号可能是乱序的。

格式

输入格式

输入共

第

接下来

输出格式

按照事件输入的顺序，每一个事件输出一行一个整数，表示这个离队事件中离队学生的编号。

样例1

样例输入1

样例输出1

1
1
4

限制

对于 $100\\%100% 的数据，nle 3 imes 10^5n≤3×105，mle 3 imes 10^5m≤3×105，qle 3 imes 10^5q≤3×105。$

数据保证每一个事件满足

以上是关于noip2017的主要内容，如果未能解决你的问题，请参考以下文章

noip2017

小凯的疑惑

描述

格式

输入格式

输出格式

样例1

样例输入1

样例输出1

提示

限制

时间复杂度

描述

格式

输入格式

输出格式

样例1

样例输入1

样例输出1

限制

逛公园

描述

格式

输入格式

输出格式

样例1

样例输入1

样例输出1

限制

奶酪

描述

格式

输入格式

输出格式

样例1

样例输入1

样例输出1

限制

宝藏

描述

格式

输入格式

输出格式

样例1

样例输入1

样例输出1

样例2

样例输入2

样例输出2

限制

描述

格式

输入格式

输出格式

样例1

样例输入1

样例输出1

限制

列队

描述

格式

输入格式

输出格式

样例1

样例输入1

样例输出1

限制