差分约束
Posted bigyellowdog
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了差分约束相关的知识,希望对你有一定的参考价值。
一、何为差分约束系统:
差分约束系统(system of difference constraints),是求解关于一组变数的特殊不等式组之方法。如果一个系统由n个变量和m个约束条件组成,其中每个约束条件形如xj-xi<=bk(i,j∈[1,n],k∈[1,m]),则称其为差分约束系统(system of difference constraints)。亦即,差分约束系统是求解关于一组变量的特殊不等式组的方法。
通俗一点地说,差分约束系统就是一些不等式的组,而我们的目标是通过给定的约束不等式组求出最大值或者最小值或者差分约束系统是否有解。
比如:
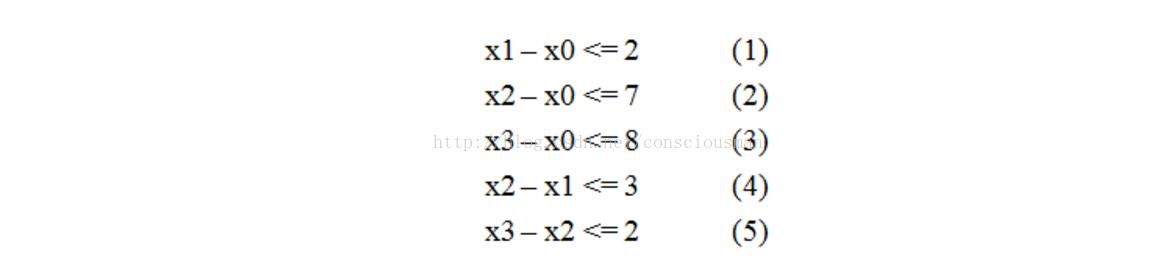
二、差分约束系统的求解:
差分约束系统可以转化为图论来解决,对应于上面的不等式组,如果要求出x3-x0的最大值的话,叠加不等式可以推导出x3-x0<=7,最大值即为7,我们可以通过建立一个图,包含6个顶点,对每个xj-xi<=bk,建立一条i到j的有向边,权值为bk。通过求出这个图的x0到x3的最短路可以知道也为7,这是巧合吗?并不是。
之所以差分约束系统可以通过图论的最短路来解,是因为xj-xi<=bk,会发现它类似最短路中的三角不等式d[v] <=d[u]+w[u,v],即d[v]-d[u]<=w[u,v]。而求取最大值的过程类似于最短路算法中的松弛过程。
三角不等式:(在此引用大牛的博客)
B - A <= C (1)
C - B <= A (2)
C - A <= B (3)
- 如果要求C-A的最大值,可以知道max(C-A)= min(b,a+c),而这正对应了下图中C到A的最短路。
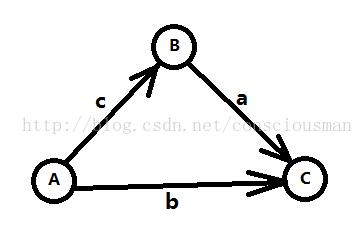
因此,对三角不等式加以推广,变量n个,不等式m个,要求xn-x1的最大值,便就是求取建图后的最短路。
同样地,如果要求取差分约束系统中xn-x1的最小值,便是求取建图后的最长路。最长路可以通过spfa求出来,只需要改下松弛的方向即可,即if(d[v] < d[u] + dist(u,v)) d[v] = d[u] + dist(u,v)。当然我们可以把图中所有的边权取负,求取最短路,两者是等价的。
最长路求解算法证明如下:
http://www.cnblogs.com/g0feng/archive/2012/09/13/2683880.html
- 最后一点,建图后不一定存在最短路/最长路,因为可能存在无限减小/增大的负环/正环,题目一般会对应于不同的输出。判断差分约束系统是否存在解一般判环即可。
3、差分约束系统的应用
差分约束系统的应用很广,都会有一定的背景,我们只需要根据题意构造出差分约束系统,然后再根据题目的要求求解就行了。
一般题目会有三种情况:(1)、求取最短路 (2)、求取最长路 (3)、判断差分约束系统的解是否存在
当然这三种也可能会相互结合。
差分约束系统的解法如下:
根据条件把题意通过变量组表达出来得到不等式组,注意要发掘出隐含的不等式,比如说前后两个变量之间隐含的不等式关系。
进行建图:
首先根据题目的要求进行不等式组的标准化。
如果要求取最小值,那么求出最长路,那么将不等式全部化成xi – xj >= k的形式,这样建立j->i的边,权值为k的边,如果不等式组中有xi – xj > k,因为一般题目都是对整形变量的约束,化为xi – xj >= k+1即可,如果xi – xj = k呢,那么可以变为如下两个:xi – xj >= k, xi – xj <= k,进一步变为xj – xi >= -k,建立两条边即可。
如果求取的是最大值,那么求取最短路,将不等式全部化成xi – xj <= k的形式, 这样建立j->i的边,权值为k的边,如果像上面的两种情况,那么同样地标准化就行了。
如果要判断差分约束系统是否存在解,一般都是判断环,选择求最短路或者最长路求解都行,只是不等式标准化时候不同,判环地话,用spfa即可,n个点中如果同一个点入队超过n次,那么即存在环。
值得注意的一点是:建立的图可能不联通,我们只需要加入一个超级源点,比如说求取最长路时图不联通的话,我们只需要加入一个点S,对其他的每个点建立一条权值为0的边图就联通了,然后从S点开始进行spfa判环。最短路类似。
- 建好图之后直接spfa或bellman-ford求解,不能用dijstra算法,因为一般存在负边,注意初始化的问题。
下面通过几个题来体会下上面的解题思路:
(1)、求取最小值
1、poj 1201- Intervals
题意:给定n个区间,[ai,bi]这个区间至少选选出ci个整数,求一个集合z,满足每个区间的要求,输出集合z的大小。
分析:令d[i]表示0到i这个区间内至少要选出d[i]个数,那么对于每个[ai,bi],有d[b] - d[ai-1] >= ci,同时隐含的一个条件是0 <= d[i] - d[i-1] <= 1,但是因此d[-1]不能表示,令d[i+1]示0到i这个区间内至少要选出d[i+1]个数,然后d[0] = 0,直接求取最长路就行了。边的存储使用链式向前星,这样效率最高。
#include <cstdio>
#include <cstring>
#include <queue>
#include <cctype>
#include <algorithm>
using namespace std;
template<class T>
inline void read(T &res) {
char c; res = 0;
while (!(isdigit(c = getchar())));
while (isdigit(c)) res = res * 10 + c - '0', c = getchar();
}
const int N = 50005;
const int INF = 0x3f3f3f3f;
int head[N], vis[N], d[N];
struct edge{
int v, d, next;
edge(int v = 0, int d = 0, int n = 0) : v(v), d(d), next(n){}
}e[N<<2];
int n, ma, mi = INF, k;
queue<int> q;
void add(int u, int v, int d) {
e[k] = edge(v, d, head[u]);
head[u] = k++;
}
int spfa() {
fill(d+mi+1, d+ma+1, -INF);
vis[mi] = 1;
q.push(mi);
while (!q.empty()) {
int t = q.front(); q.pop();
vis[t] = 0;
for (int i = head[t]; i != -1; i = e[i].next) {
int x = e[i].v;
if (d[x] < d[t] + e[i].d) {
d[x] = d[t] + e[i].d;
if (!vis[x]) vis[x] = 1, q.push(x);
}
}
}
return d[ma];
}
int main() {
int k = 0;
memset(head, -1, sizeof(head));
read(n);
for (int i = 0; i < n; i++) {
int a, b, c;
read(a); read(b); read(c);
add(a, b+1, c);
ma = max(ma, b); mi = min(mi, a);
}
ma++;
for (int i = mi; i < ma; i++) add(i, i+1, 0), add(i+1, i, -1);
printf("%d
", spfa());
return 0;
}2、poj1275 - Cashier Employment
题意:在一家超市里,每个时刻都需要有营业员看管,R(i) (0 <= i < 24)表示从i时刻开始到i+1时刻结束需要的营业员的数目,现在有N(N <= 1000)个申请人申请这项工作,并且每个申请者都有一个起始工作时间 ti,如果第i个申请者被录用,那么他会从ti时刻开始连续工作8小时。现在要求选择一些申请者进行录用,使得任何一个时刻i,营业员数目都能大于等于R(i)。求出至少需要录用多少营业员。
分析:每天的工作情况都是一样的,我们只需要求出一天的即可。根据题意,令s[i]为一天内前i+1个小时录用的人数,如果i>=7,则s[i] - s[i-8] >= R[i],如果0 <= i < 7,则可以推出s[23] - s[i+16] + s[i] >= R[i],同时每个时刻录用的人数有个上限,假设第i时刻最多可以录用的人数为b[i],则对于每一个i有0 <=s[i] - s[i-1] <= b[i]。
现在需要解决的一个问题是,第二个不等式中包含3个s组的变量,这该怎么建图呢?可以知道我们只需要枚举s[23],那么这个量就是已知的了,因此不等式可以变为s[i] - s[i+16] >= R[i] - s[23],但是必须明白的一点是,既然s[23]是枚举的一天的录用人数的最小数目,我们建图之后求出的s[23]也应该为枚举的那个值,可以从0到n枚举s[23],第一个值便是答案,但是可以更高效地求解,因为问题具有单调性,直接二分.
因为s[-1] = 0,-1无法表示,只需要向右移动一个单位即可,那么令s[0] = 0,思路很清晰了,二分s[24]搜索最小值。
#include <cstdio>
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
const int N = 30, M = 1010;
const int INF = 0x3f3f3f3f;
struct edge{
int v, d, next;
edge(int v, int d, int n):v(v), d(d), next(n){}
edge(){}
}ed[M];
int head[N], d[N], vis[N], R[N], tim[N], k;
queue<int> q;
void init() {
k = 0;
memset(head, -1, sizeof(head));
memset(d, -INF, sizeof(d));
memset(vis, 0, sizeof(vis));
while (!q.empty()) q.pop();
}
void add(int u, int v, int d) {
ed[k] = edge(v, d, head[u]);
head[u] = k++;
}
int cal(int m) {
q.push(0); d[0] = 0;
while (!q.empty()) {
int x = q.front(); q.pop();
vis[x] = 0;
if (x == 24 && d[x] > m) return 0;
for (int i = head[x]; i != -1; i = ed[i].next) {
int t = ed[i].v;
if (d[t] < d[x] + ed[i].d) {
d[t] = d[x] + ed[i].d;
if (!vis[t]) vis[t] = 1, q.push(t);
}
}
}
return d[24] == m ? 1 : 0;
}
int main() {
int t;
scanf("%d", &t);
while (t--) {
for (int i = 0; i < 24; i++) scanf("%d", R+i);
int n;
scanf("%d", &n);
memset(tim, 0, sizeof(tim));
for (int i = 0; i < n; i++) {
int tmp;
scanf("%d", &tmp);
tim[tmp]++;
}
int r = n+1, l = -1;
while (r - l > 1) {
int m = (r + l) / 2;
init();
for (int i = 0; i <= 23; i++) add(i+1, i, -tim[i]), add(i, i+1, 0);
for (int i = 7; i <= 23; i++) add(i-7, i+1, R[i]);
add(0, 24, m); add(24, 0, -m);
for (int i = 0; i < 7; i++) add(i+17, i+1, R[i]-m);
cal(m) ? r = m : l = m;
}
l >= n ? puts("No Solution") : printf("%d
", r);
}
return 0;
}(2)、求取最大值
1、hdu3440 - House man
题意:有n栋房子,给出每栋房子的高度和开始时的相对位置,可以移动一些房子,但不能改变这些房子的相对位置,现在从最矮的房子开始,每次跳至比它高的第一栋房子, 而且每次跳跃的水平距离最大是D,房子不能在同一位置,只能在整点位置。问最矮的房子和最高的房子之间的最大距离可以是多少?如果不能从最矮的房子到达最高的房子则输出-1.
分析:令d[i]表示第i栋房子与第一栋房子之间的最大距离,那么我们要求的就是的的d[n],求最短路即可,首先每栋房子之间的相对位置已经确定且不能在同一位置,那么d[i+1] > d[i],每次要跳至比它高的房子上,那么我们需要对房子按高度排序。因为开始时已经规定标号小的点在标号大的点的左边,这样,我们如果从标号大的点到标号小的点,建一条这样的边就会有问题,只能按小到大建边,而且如果两个排序后相邻房子之间的标号大于D的话则不可能到最高的房子,因为房子不可能在同一位置,他们之间的距离至少是D。约束条件只有这两者,建边时需要处理一下方向。最后如果最高的房子标号比矮的房子小的话,则以最高的房子为源点进行spfa,如果存在负环则输出-1.
因此建图不能一概而论,还是要思考前后的联系。建图也算是图论题的一个重要部分吧。
#include <bits/stdc++.h>
using namespace std;
const int N = 1010, M = 10000;
const int INF = 0x3f3f3f3f;
struct house{
int he, id;
bool operator < (const house& x)const { return he < x.he; }
}h[N];
struct edge{
int v, d, next;
edge(int v, int d, int n):v(v), d(d), next(n){}
edge(){}
}ed[M];
int head[N], d[N], vis[N], cnt[N];
int n, s, e, k;
queue<int> q;
void init() {
k = 0;
memset(head, -1, sizeof(int) * n);
memset(d, INF, sizeof(int) * n);
memset(vis, 0, sizeof(int) * n);
memset(cnt, 0, sizeof(int) * n);
for (int i = 0; i < n; i++) h[i].id = i;
while (!q.empty()) q.pop();
}
void add(int u, int v, int d) {
ed[k] = edge(v, d, head[u]);
head[u] = k++;
}
int spfa() {
d[s] = 0; cnt[s]++;
q.push(s);
while (!q.empty()) {
int x = q.front(); q.pop();
vis[x] = 0;
for (int i = head[x]; i != -1; i = ed[i].next) {
int t = ed[i].v;
if (d[t] > d[x] + ed[i].d) {
d[t] = d[x] + ed[i].d;
if (!vis[t]) {
vis[t] = 1; q.push(t);
if (++cnt[t] > n) return -1;
}
}
}
}
return d[e];
}
int main() {
int t, ca = 0;
scanf("%d", &t);
while (t--) {
int d;
scanf("%d %d", &n, &d);
init();
for (int i = 0; i < n; i++) scanf("%d", &h[i].he);
sort(h, h+n);
int flag = 1;
for (int i = 0; i < n-1 && flag; i++) {
add(i+1, i, -1);
int u = min(h[i].id, h[i+1].id), v = max(h[i].id, h[i+1].id);
if (v - u > d) flag = 0;
add(u, v, d);
}
s = min(h[0].id, h[n-1].id), e = max(h[0].id, h[n-1].id);
printf("Case %d: %d
", ++ca, flag ? spfa() : -1);
}
return 0;
}2、poj3169 - Layout
题意:有n头牛,他们按顺序排成了一排,有些牛关系比较好,他们的距离不能超过某个距离,还有些牛关系不好,他们之间的距离不能小于某个距离,可能会有多头牛挤在同一位置上,问1号牛和n号牛之间的最大距离是多少,如果不存在满足条件的排列则输出-1,如果距离无限大则输出-2.
分析:令d[i]表示第i头牛的位置,因为牛按顺序排列,则有d[i] <= d[i+1],关系好的牛有d[a] +D >= d[b], 关系不好的牛有d[a] + d <= d[b],把不等式标准化之后直接跑最短路即可。
如果无限大则输出-2,不存在排列输出-1.
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1010, M = 100010;
const int INF = 0x3f3f3f3f;
struct edge{ int v, d; };
vector<edge> G[N];
queue<int> q;
int d[N], vis[N], cnt[N];
int spfa(int n) {
fill(d + 2, d + 1 + n, INF);
q.push(1);
while (!q.empty()) {
int u = q.front(); q.pop();
vis[u] = 0;
for (int i = 0; i < G[u].size(); i++) {
edge e = G[u][i];
int v = e.v;
if (d[u] + e.d < d[v]) {
d[v] = d[u] + e.d;
if(!vis[v]) {
if(++cnt[v] > n) return -1;
q.push(v); vis[v] = 1;
}
}
}
}
return d[n] == INF ? -2 : d[n];
}
int main() {
int n, ml, md, u, v, d;
scanf("%d %d %d", &n, &ml, &md);
for(int i = 0; i < ml; i++) {
scanf("%d %d %d", &u, &v, &d);
G[u].push_back((edge){v, d});
}
for(int i = 0; i < md; i++) {
scanf("%d %d %d", &u, &v, &d);
G[v].push_back((edge){u, -d});
}
for(int i = 1; i < n; i++) G[i+1].push_back((edge){i, 0});
printf("%d
", spfa(n));
return 0;
}(3)、判断解是否存在
1、poj1364 - KIng
题意: 给定一个序列a1, a2, ..., an,给出它的一些子序列以及对该子序列的约束条件,例如asi, asi+1, asi+2, ..., asi+ni,且asi+asi+1+asi+2+......+asi+ni 小于或者大于 ki。求是否存在满足以上要求的数列。是 则输出“lamentable kingdom”,否则输出“successful conspiracy”。
分析:判断解是否存在只要判正环就行了,很明显,题目需要从区间和下手,令S[i]为1到i这i个元素的和,那么根据题意建立不等式然后建图,s[si+ni] - s[si-1] > k,或者s[si+ni] - s[si-1] < k最后加入一个源点,然后对每个点i建立一条权为0的边.如果不存在环则解一定存在。当然求最短路判负环也可以。
#include <cstdio>
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
const int N = 110, M = 1000;
const int INF = 0x3f3f3f3f;
struct edge{
int v, d, next;
edge(int v, int d, int n):v(v), d(d), next(n){}
edge(){}
}ed[M];
int head[N], d[N], vis[N], cnt[N], k;
queue<int> q;
void init() {
k = 0;
memset(head, -1, sizeof(head));
memset(d, INF, sizeof(d));
memset(vis, 0, sizeof(vis));
memset(cnt, 0, sizeof(cnt));
while (!q.empty()) q.pop();
}
void add(int u, int v, int d) {
ed[k] = edge(v, d, head[u]);
head[u] = k++;
}
int spfa(int n) {
d[n+1] = 0; cnt[n+1]++;
q.push(n+1);
while (!q.empty()) {
int x = q.front(); q.pop();
vis[x] = 0;
for (int i = head[x]; i != -1; i = ed[i].next) {
int t = ed[i].v;
if (d[t] > d[x] + ed[i].d) {
d[t] = d[x] + ed[i].d;
if (!vis[t]) {
vis[t] = 1; q.push(t);
if (++cnt[t] > n+2) return 0;
}
}
}
}
return 1;
}
int main() {
int n, m;
while (scanf("%d", &n), n) {
init();
scanf("%d", &m);
for (int i = 0; i < m; i++) {
int si, ni, ki;
char o[100];
scanf("%d %d %s %d", &si, &ni, o, &ki);
o[0] == 'g' ? add(si+ni, si-1, -ki-1) : add(si-1, si+ni, ki-1);
}
for (int i = 0; i <= n; i++) add(n+1, i, 0);
puts(spfa(n) ? "lamentable kingdom" : "successful conspiracy");
}
return 0;
}poj2983 - Is the Information Reliable?
题意:银河系中有n个防御站排成一条直线,给定m条信息,每条信息的格式如下。
P A B X代表A站在B站北方X光年处。
V A B 代表A站在B站北方,而且距离至少为1光年。
问是否存在这样的一个防御战排列满足上述要求,是输出Reliable,否输出 Unreliable。
分析:同上题一样,令d[i]表示第i号防御站的位置,根据信息建立不等式,然后根据选择的判环方式建边,然后加入源点s,对每个点建立一条长为0的边。直接spfa判环即可。
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
#include <cctype>
using namespace std;
const int N = 1005;
const int M = 100005;
const int INF = 0x3f3f3f3f;
struct edge{
int v, d, next;
edge(int v, int d, int n) : v(v), d(d), next(n){}
edge(){}
}e[2*M + N];
int head[N], d[N], vis[N], cnt[N];
int n, m, k;
queue<int> q;
template<class T>
inline int read(T &res) {
char c; res = 0;
while (!(isdigit(c = getchar())));
while (isdigit(c)) res = res * 10 + c - '0', c = getchar();
return 1;
}
void add(int u, int v, int d) { e[k] = edge(v, d, head[u]); head[u] = k++; }
void init(int n) {
k = 0;
memset(cnt, 0, sizeof(int) * (n+3));
memset(vis, 0, sizeof(int) * (n+3));
memset(head, -1, sizeof(int) * (n+3));
while (!q.empty()) q.pop();
fill(d+1, d+1+n, -INF);
}
bool spfa() {
vis[0] = 1;
q.push(0); cnt[0]++;
while (!q.empty()) {
int x = q.front(); q.pop();
vis[x] = 0;
for (int i = head[x]; i != -1; i = e[i].next) {
int t = e[i].v;
if (d[t] < d[x] + e[i].d) {
d[t] = d[x] + e[i].d;
if (!vis[t]) {
vis[t] = 1; q.push(t);
if (++cnt[t] > n) return 0;
}
}
}
}
return 1;
}
int main() {
while (~scanf("%d %d", &n, &m)) {
char s[10];
init(n);
for (int i = 0; i < m; i++) {
int a, b, x = 1;
scanf("%s", s);
read(a); read(b);
if (s[0] == 'P') read(x);
add(a, b, x);
if (s[0] == 'P') add(b, a, -x);
}
for (int i = 1; i <= n; i++) add(0, i, 0);
puts(spfa() ? "Reliable" : "Unreliable");
}
return 0;
}关于差分约束的更详细的讲解可以参考下面这位大牛的博客,而且还有很多练习题。
http://www.cppblog.com/menjitianya/archive/2015/11/19/212292.html
文章转载自→
以上是关于差分约束的主要内容,如果未能解决你的问题,请参考以下文章