CodeForces 232C Doe Graphs

Posted 2021-01-16 coder-uranus

CF232C Doe Graphs

题意

题意翻译

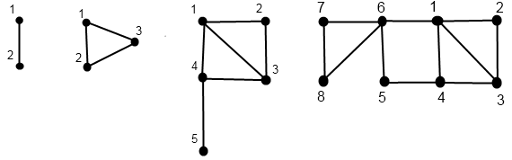
(Doe)以她自己的名字来命名下面的无向图

(D(0))是只有一个编号为(1)的结点的图.

(D(1))是只有两个编号分别为(1)和(2)的点与一条连接这两个点的边的图.

(D(n))以如下方法构造

将(D(n-2))中所有点的编号加上(|D(n-1)|)

在点(|D(n-1)|)与点(|D(n-1)|+1)之间连边。

在点(|D(n-1)|+1)与点1之间连边

现在(Doe)已经构造出了(D(n)(nleq 100)),她会多次询问你在这张图中(a b)两点间的最短路

输入输出格式

输入格式：

The first line contains two integers (t) and (n) ( (1leq tleq 10^{5}; 1leq nleq 10^{3}) ) — the number of queries and the order of the given graph. The (i)-th of the next (t) lines contains two integers (a_{i}) and (b_{i}) ( (1leq a_{i},b_{i}leq 10^{16}, a_{i} eq b_{i}) ) — numbers of two vertices in the (i)-th query. It is guaranteed that (a_{i},b_{i}leq |D(n)|).

Please, do not use the %lld specifier to read or write 64-bit integers in С++. It is preferred to use cin, cout streams or the %I64d specifier.

输出格式：

For each query print a single integer on a single line — the length of the shortest path between vertices (a_{i}) and (b_{i}). Print the answers to the queries in the order, in which the queries are given in the input.

输入输出样例

输入样例#1：

10 5
1 2
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5
4 5

输出样例#1：

1
1
1
2
1
2
3
1
2
1

思路

首先想到，每张图的点的数量是有规律的：

[V(D(n))=V(D(n-1))+V(D(n-2))]

这不就是斐波那契数列吗？我们不妨直接记(F(n))为(D(n))的顶点数。

然后考虑查询两点(a b)在(D(n))中的最短路，一开始我的想法是这样的：如果有(1leq a,bleq F(n-1))，那么(a b)在(D(n))中的最短路也就是在(D(n-1))中的最短路；如果有(F(n-1)< a,bleq F(n))，那么(a b)在(D(n))中的最短路也就是在(D(n-2))中的最短路。其余的情况再分治下去。但是这是有问题的，因为有的时候两点可以绕到下一张图上去，然后再绕回一张图中，这样的距离可能会更短。

具体来说，一共有这几种情况：

• (a b)都在(D(n-1))的范围内：
  • (a)直接走图(D(n-1))到达(b)；
  • (a)通过点(1)走到图(D(n-2))，再绕回到图(D(n-1))，到达(b)；
  • (a)通过点(F(n-1))走到图(D(n-2))，再绕回到图(D(n-1))，到达(b)。
• (a b)都在(D(n-2))的范围内：
  • (a)直接走图(D(n-2))到达(b)。
• (a)在(D(n-1))范围内，而(b)在(D(n-2))范围内：
  • (a)通过点(1)走到图(D(n-2))，再走到(b)；
  • (a)通过点(F(n-1))走到图(D(n-2))，再走到(b)。

那么我们就可以在搜索的过程中分类讨论来优化了。

但是这样还是会(TLE)。接下来，我们发现有多次重复询问是关于(a)点如何最快到达(1)点或者(F(n-1))点，我们就可以先把它预处理出来，再搜索。具体实现见代码。

AC代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL n,m,f[1005],d[1005],d1[1005],d2[1005],d3[1005],d4[1005];
LL read()
{
    LL re=0;char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) re=(re<<3)+(re<<1)+ch-'0',ch=getchar();
    return re;
}
void prework(LL x,LL g,LL *a1,LL *a2)
{
    if(!g){a1[g]=a2[g]=0;return ;}
    if(g==1){a1[g]=(x==2),a2[g]=(x==1);return ;}
    if(x<=f[g-1])
    {
        prework(x,g-1,a1,a2);
        a1[g]=min(a1[g-1],a2[g-1]+2);
        a2[g]=min(a1[g-1],a2[g-1])+1+d[g-2];
    }
    else
    {
        prework(x-f[g-1],g-2,a1,a2);
        a1[g]=a1[g-2]+1;
        a2[g]=a2[g-2];
    }
}
LL ask(LL g,LL x,LL y)
{
    if(g<=1) return x!=y;
    if(x<=f[g-1]&&y<=f[g-1]) return min(ask(g-1,x,y),min(d1[g-1]+d4[g-1],d2[g-1]+d3[g-1])+2);
    if(x<=f[g-1]&&y>f[g-1]) return min(d1[g-1],d2[g-1])+1+d3[g-2];
    else return ask(g-2,x-f[g-1],y-f[g-1]);
}
int main()
{
    f[0]=1,f[1]=2,d[0]=0,d[1]=1;
    for(LL i=2;i<80;i++) f[i]=f[i-1]+f[i-2],d[i]=d[i-2]+1;
    m=read(),n=min(read(),LL(80));
    while(m--)
    {
        LL x=read(),y=read();if(x>y) swap(x,y);
        prework(x,n,d1,d2);prework(y,n,d3,d4);
        printf("%lld
",ask(n,x,y));
    }
    return 0;
}