CF1000G Two-Paths

Posted 2021-01-16 liguanlin1124

题目大意：给你一棵树，其中点上和边上都有值。定义2-Path为经过一条边最多两次的路径，价值为经过点的权值加和-经过边权值*该边经过次数。4e5组询问，每次询问树上连接x,y两点的2-Path的最大价值。

题解：

一道状态比较多的树形dp。

dp1:记录x点子树内从x到x的最大2-Path的价值-x的值。

dp2:记录从fa[x]到fa[x]不经过x且不经过fa[fa[x]]的最大2-Path价值-fa[x]的值。

dp3:记录从fa[x]到fa[x]不经过x的任意儿子的2-Path的价值-x的值。

（描述比较恶心，见图）

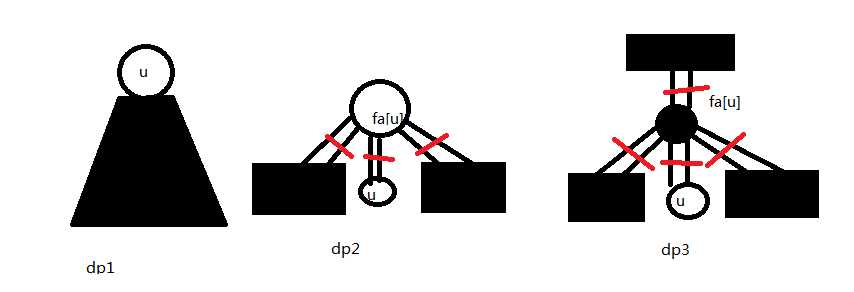
（图也比较恶心）

红色的边和涂黑的未知物体都要取。

然后还有比较大众的ds1:记录x到根的点权之和，和ds2:记录x到根的边权之和。

还要求一下每个点到根节点经过点的dp2之和。

dfsO(n)搞dp，询问O(nlogn)。

比描述和图片更恶心的代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 300050
#define Q 400050
#define ll long long
int n,q,hed[N],cnt;
struct EG
{
    int to,nxt;
    ll val;
}e[2*N];
void ae(int f,int t,ll v)
{
    e[++cnt].to = t;
    e[cnt].val = v;
    e[cnt].nxt = hed[f];
    hed[f] = cnt;
}
ll a[N];
int dep[N],fa[N][25];
ll ds1[N],ds2[N],E[N];
void dfs1(int u,int f)
{
    dep[u]=dep[f]+1;
    for(int j=hed[u];j;j=e[j].nxt)
    {
        int to = e[j].to;
        if(to==f)continue;
        fa[to][0]=u;
        E[to]=e[j].val;
        ds1[to]=ds1[u]+a[to];
        ds2[to]=ds2[u]+e[j].val;
        dfs1(to,u);
    }
}
int get_lca(int x,int y)
{
    if(dep[x]<dep[y])swap(x,y);
    for(int i=20;i>=0;i--)
        if(dep[fa[x][i]]>=dep[y])
            x=fa[x][i];
    if(x==y)return x;
    for(int i=20;i>=0;i--)
        if(fa[x][i]!=fa[y][i])
            x=fa[x][i],y=fa[y][i];
    return fa[x][0];
}
ll dp1[N],dp2[N];
bool vis[N];
void dfs(int u)
{
    for(int j=hed[u];j;j=e[j].nxt)
    {
        int to = e[j].to;
        if(to==fa[u][0])continue;
        dfs(to);
        if(dp1[to]+a[to]-2ll*e[j].val>=0)
        {
            dp1[u]+=dp1[to]+a[to]-2ll*e[j].val;
            vis[to]=1;
        }
    }
    for(int j=hed[u];j;j=e[j].nxt)
    {
        int to = e[j].to;
        if(to==fa[u][0])continue;
        if(!vis[to])dp2[to]=dp1[u];
        else dp2[to]=dp1[u]-(dp1[to]+a[to]-2ll*e[j].val);
    }
}
ll dp3[N],sum2[N];
void Dfs(int u)
{
    sum2[u]+=dp2[u];
    for(int j=hed[u];j;j=e[j].nxt)
    {
        int to = e[j].to;
        if(to==fa[u][0])continue;
        sum2[to]+=sum2[u];
        dp3[to]=max(0ll,dp3[u]+1ll*a[u]+dp2[to]-2ll*e[j].val);
        Dfs(to);
    }
}
ll sol(int x,int y)
{
    if(dep[x]>dep[y])swap(x,y);
    int lca = get_lca(x,y);
    if(x==lca)
    {
        return dp3[x]+dp1[y]+sum2[y]-sum2[x]+(ds1[x]+ds1[y]-ds1[lca]-ds1[fa[lca][0]])-(ds2[x]+ds2[y]-2ll*ds2[lca]);
    }else
    {
        int ffx = x,ffy = y;
        for(int i=20;i>=0;i--)
        {
            if(dep[fa[ffx][i]]>dep[lca])
                ffx=fa[ffx][i];
            if(dep[fa[ffy][i]]>dep[lca])
                ffy=fa[ffy][i];
        }
        return dp1[x]+dp1[y]+sum2[x]+sum2[y]-sum2[ffx]-sum2[ffy]+dp3[lca]+dp2[ffx]-(vis[ffy]==1)*(dp1[ffy]+a[ffy]-2ll*E[ffy])+(ds1[x]+ds1[y]-ds1[lca]-ds1[fa[lca][0]])-(ds2[x]+ds2[y]-2ll*ds2[lca]);
    }
}
int main()
{
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
    ll v;
    for(int f,t,i=1;i<n;i++)
    {
        scanf("%d%d%lld",&f,&t,&v);
        ae(f,t,v),ae(t,f,v);
    }
    ds1[1]=a[1];
    dfs1(1,1);
    for(int k=1;k<=20;k++)
        for(int i=1;i<=n;i++)
            fa[i][k]=fa[fa[i][k-1]][k-1];
    dfs(1);
    Dfs(1);
    for(int x,y,i=1;i<=q;i++)
    {
        scanf("%d%d",&x,&y);
        printf("%lld
",sol(x,y));
    }
    return 0;
}