二叉树和递归框架
Posted Debroon
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉树和递归框架相关的知识,希望对你有一定的参考价值。
二叉树和递归模式
二叉树递归细节
递归有两大要点:反复调用自身、终止条件。
在二叉树递归,这两点变为:递归调用自己两个子树、在叶结点处终止递归。
细节1:空树的两种含义
void dfs(TreeNode* root)
if (root == NULL) return; // 空树:整个树为空、遍历到叶结点下的两个空子树
- 第一个含义是整棵树都为空,我们用 root == null 作为递归的终止条件。
- 第二个含义是某个子树为空。由于函数是递归调用的,参数 root 可以表示任何一个子树。特别的,叶结点的两个子树都为空,递归到这里就会自然遇到两个 root == null 的情况。叶子节点为空,我们用 root == null 作为递归的终止条件。
细节2:凡是题目描述里提到叶结点的,都需要显式判断叶结点,在叶结点处结束递归
例题:
如 112,给定一个二叉树和一个目标和,判断该树中是否存在根结点到叶结点的路径,这条路径上所有结点值相加等于目标和。
bool hasPathSum(TreeNode* root, int sum)
if (root == NULL) return sum == 0;
int target = sum - root->val;
return hasPathSum(root->left, target) || hasPathSum(root->right, target);
可当树为空树、sum = 0 时,会错误地返回 true。
bool hasPathSum(struct TreeNode* root, int sum)
if( root == NULL ) return false;
// 凡是题目描述里提到叶结点的,都需要显式判断叶结点,在叶结点处结束递归
if( root->left == NULL && root->right == NULL ) // 显式判断叶结点:在叶结点的两个空子树处判断并结束递归,改为在叶结点处进行判断并结束递归
return (root->val - sum) == 0;
return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);
细节3:使用全局变量的时机
如果题目所求的结果涉及到所有子树上的子问题,而不仅仅是根结点上的子问题,考虑使用全局变量。
如果题目要返回的结果就是所有子树的最大值,或是所有子树的和,那么可以在遍历的过程中不断更新变量,让代码更简洁。
不过算法竞赛经常被人诟病的原因之一就是,全局变量乱开。
我们还可以用一些特殊的函数参数,达到和全局变量一样的效果。
- C++ 的引用类型参数 void dfs(int& res)
- Java 使用长度为 1 的数组,元素分配在堆上 int[] res = new int[1];
int foo(TreeNode* root)
int res = 0;
traverse(root, res);
return res;
void traverse(TreeNode* root, int& res) // CPP 引用类型参数
res = 1;
细节4:参数函数扩展
如果不考虑参数扩展, 一个最简单的 dfs 通常是下面这样:
void dfs(root)
而有时候,我们需要 dfs 携带更多的有用信息。
典型的有以下三种情况:
- 携带父亲或者爷爷的信息
void dfs(root, parent)
if (root == NULL) return;
dfs(root->left, root)
dfs(root->right, root)
- 携带路径信息,可以是路径和或者具体的路径数组等
void dfs(root, path_sum) // 路径和
if (root == NULL) return path_sum; // 这里可以拿到根到叶子的路径和
dfs(root->left, path_sum + root->val)
dfs(root->right, path_sum + root->val)
def dfs(root, path) // 路径
if (root == NULL) return path; // 这里可以拿到根到叶子的路径
path.push_back(root.val)
dfs(root->left, path)
dfs(root->right, path)
path.pop()
细节5:删除二叉树节点使用虚拟节点
树的删除和链表删除类似,树的删除需要父节点。
所以,不仅仅链表有虚拟节点的技巧,树也是一样。
链表的虚拟指针的技巧,通常在什么时候才使用?
- 其中一种情况是链表的头会被修改。
这个时候通常需要一个虚拟指针来做新的头指针,这样就不需要考虑第一个指针的问题了。
树也是一样,当需要对树的头节点(在树中我们称之为根节点)进行修改的时候, 就可以考虑使用虚拟指针的技巧了。
- 另外一种是需要返回树中间的某个节点(不是返回根节点)。
也可借助虚拟节点。新建一个虚拟头,让虚拟头在恰当的时候(刚好指向需要返回的节点)断开连接,这样我们就可以返回虚拟头的 next 就 ok 了。
例题:
-
- 删除给定值的叶子节点
-
- 二叉树剪枝
- 二叉树剪枝
二叉树递归框架
二叉树的递归框架,有 5 种:
- 遍历二叉树框架
- 回溯框架
- 子问题分解框架
- 相邻节点遍历框架
- 递归转迭代框架
遍历二叉树框架
只要涉及递归的问题,都是树的问题,或者说树的遍历。
void traverse(TreeNode root) // 遍历二叉树
if (root == null) return; // 最基础的情况
//【前序位置】
traverse(root.left); // 进入左子树
//【中序位置】
traverse(root.right); // 进入右子树
//【后序位置】
把 print(root.val) 放在前序位置、中序位置、后序位置,有什么不同呢?
关键在于,时机。下图是可视化过程:
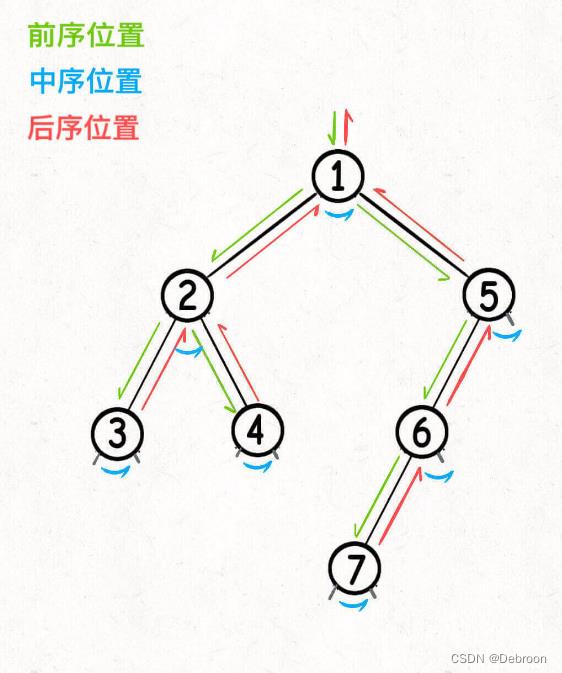
前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点:
- 前序位置的代码,进入节点前执行;
- 后序位置的代码,离开节点后执行;
- 中序位置的代码,在一个二叉树节点左子树都遍历完,即将开始遍历右子树的时候执行。
任何递归形式的遍历都有前序位置和后序位置:
void traverse(ListNode head) // 递归遍历单链表
if (head == null) return; // 最基础的情况
//【前序位置】
traverse(head.next);
//【后序位置】
那前序位置和后序位置的区别是什么?
- 前序位置能解决的问题:顺序遍历节点,遍历树/链表沿途就能计算出来结果
- 后序位置能解决的问题:倒序遍历节点,遍历完树/链表,遇到最基础的情况才能计算出来结果,即由子树的解退出原问题的解。
比如二叉树一个节点在第几层,从根节点遍历过来的过程就能顺带记录。
而以一个节点为根的整棵子树有多少个节点,需要遍历完子树之后才能数清楚。
任何递归函数,本质上都是在遍历一棵(递归)树。
- 设计每一个节点的模式(遍历二叉树模式、回溯模式、分解子问题模式下)
- 设计需要在什么时候(前\\中\\后序位置)做某事。
递归函数 = 遍历二叉树模式/回溯模式/分解子问题模式 + 前/中/后序位置 + 做某事
比如归并排序是,遍历二叉树模式 + 后序位置 + 做某事(合并数组merge),也就是二叉树的后序遍历。
void merge_sort(int a[], int l, int r)
if( l >= r ) return; // 只有一个元素,或者没有元素,不用排序
int mid = (l + r) / 2; // 分界点
merge_sort(a, l, mid); // 分治,对前半部分排序
merge_sort(a, mid+1, r); // 分治,对后半部分排序
merge(a, l, mid, r); // 【后序位置】做合并,对俩个有序数组排序
比如快速排序是,遍历二叉树模式 + 前序位置 + 做某事(中枢值划分partition),也就是二叉树的前序遍历。
void QuickSort(int arr[], int l, int r)
if( l >= r ) return;
int p = partition(arr, l, r); // 【前序位置】划枢值,p是划分中枢值的下标
QuickSort(arr, l, p-1); // 小于 p
QuickSort(arr, p+1, r); // 大于 p
有时候,我们还会同时使用【前序位置】、【后序位置】各做一些事。
void traverse(ListNode head) // 递归遍历单链表
if (head == null) return; // 最基础的情况
//【前序位置】做一些事
dfs(root.left)
dfs(root.right)
//【后序位置】做另外的事
不过我们这里只考虑「主逻辑」的位置,关键词是「主逻辑」。
如果代码主逻辑在左右子树之前执行,那么就是前序遍历。
如果代码主逻辑在左右子树之后执行,那么就是后序遍历。
回溯框架
使用场景:问题可通过遍历一棵二叉树得到答案。
ans = []
void recall( 路径,[选择列表] )
if 满足结束条件:
ans.add( 路径 )
return
for 选择 in [选择列表]:
做选择
recall( 路径,[选择列表] )
撤销选择
回溯算法都可以将决策路径画成树的形状,成为一棵搜索树。
回溯法执行的过程实际上就是在这棵树上做遍历。
回溯框架,本质是遍历一颗决策树。
- 路径:已经做出的选择
- 选择列表:当前可以做的选择
- 结束条件:到了决策树底层,无法再做选择
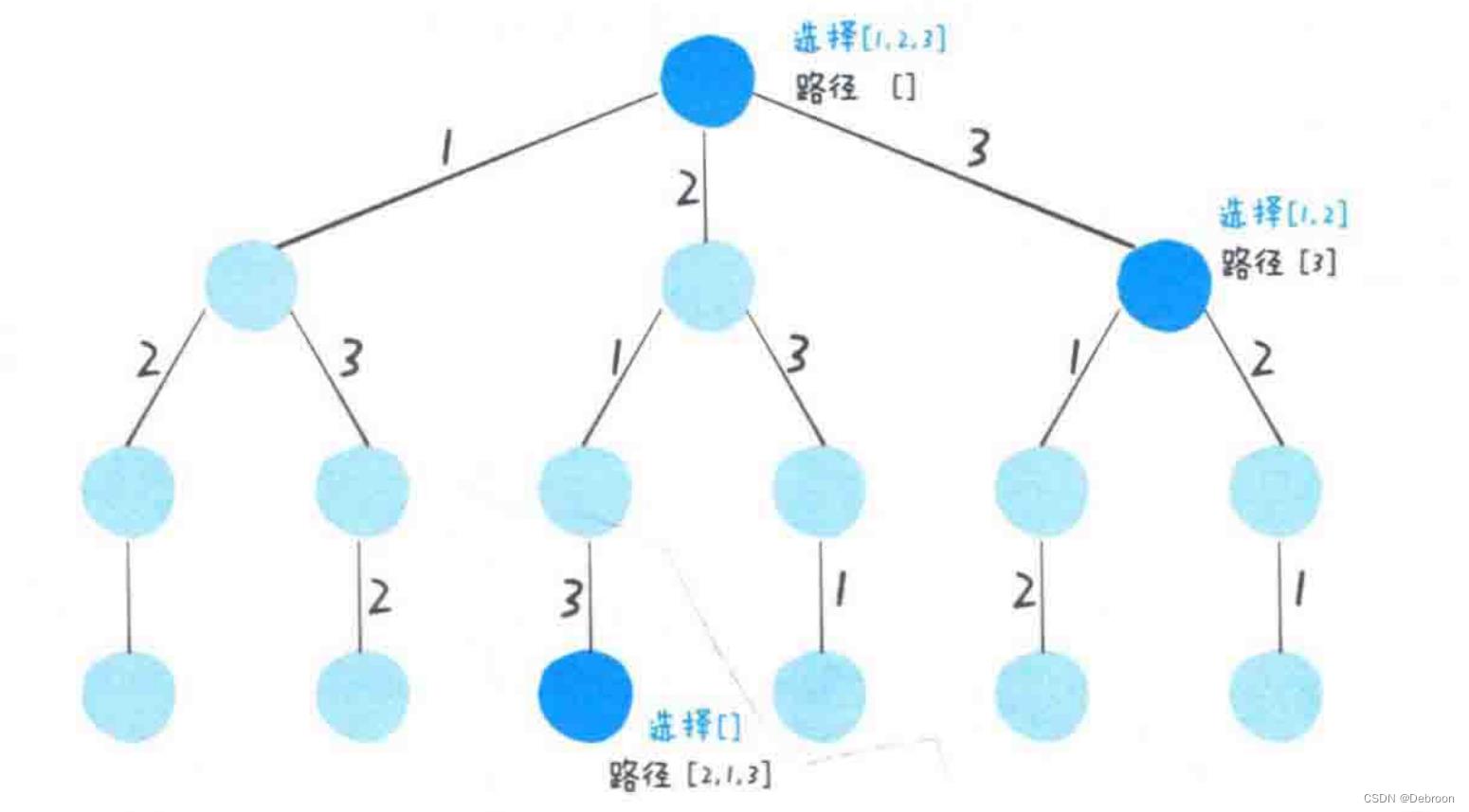
核心在于 for 循环里面的递归,在递归之前做选择,在递归之后撤销选择。
- for 循环,如果可视化就是在遍历一颗 N 叉树
问题是,选择和撤销选择是在这颗树上做什么呢?
- 选择:是在这棵树上做前序遍历
- 撤销选择:是在这颗树上做后序遍历
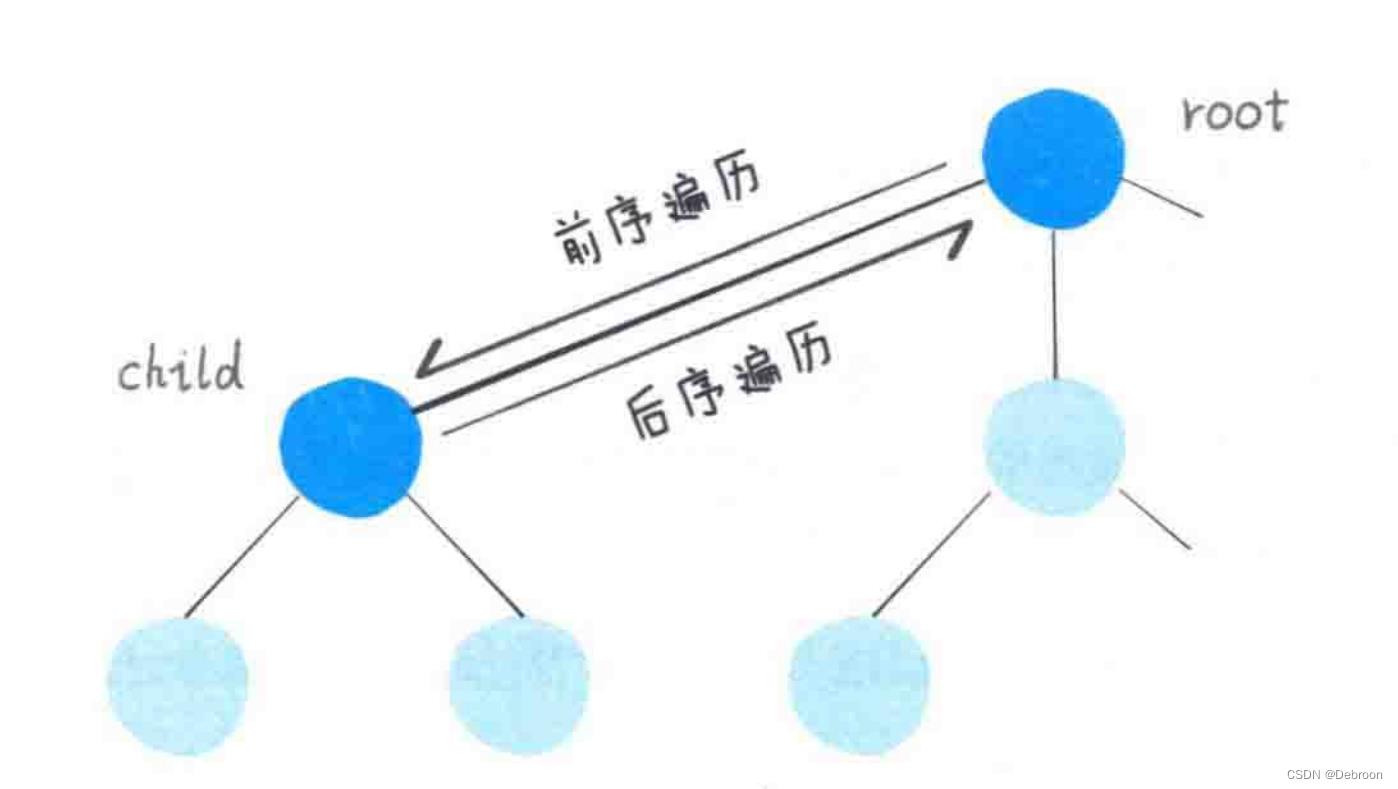
选择是,在进入树的某一节点前执行。
撤销选择是,在离开树的某一节点后执行。
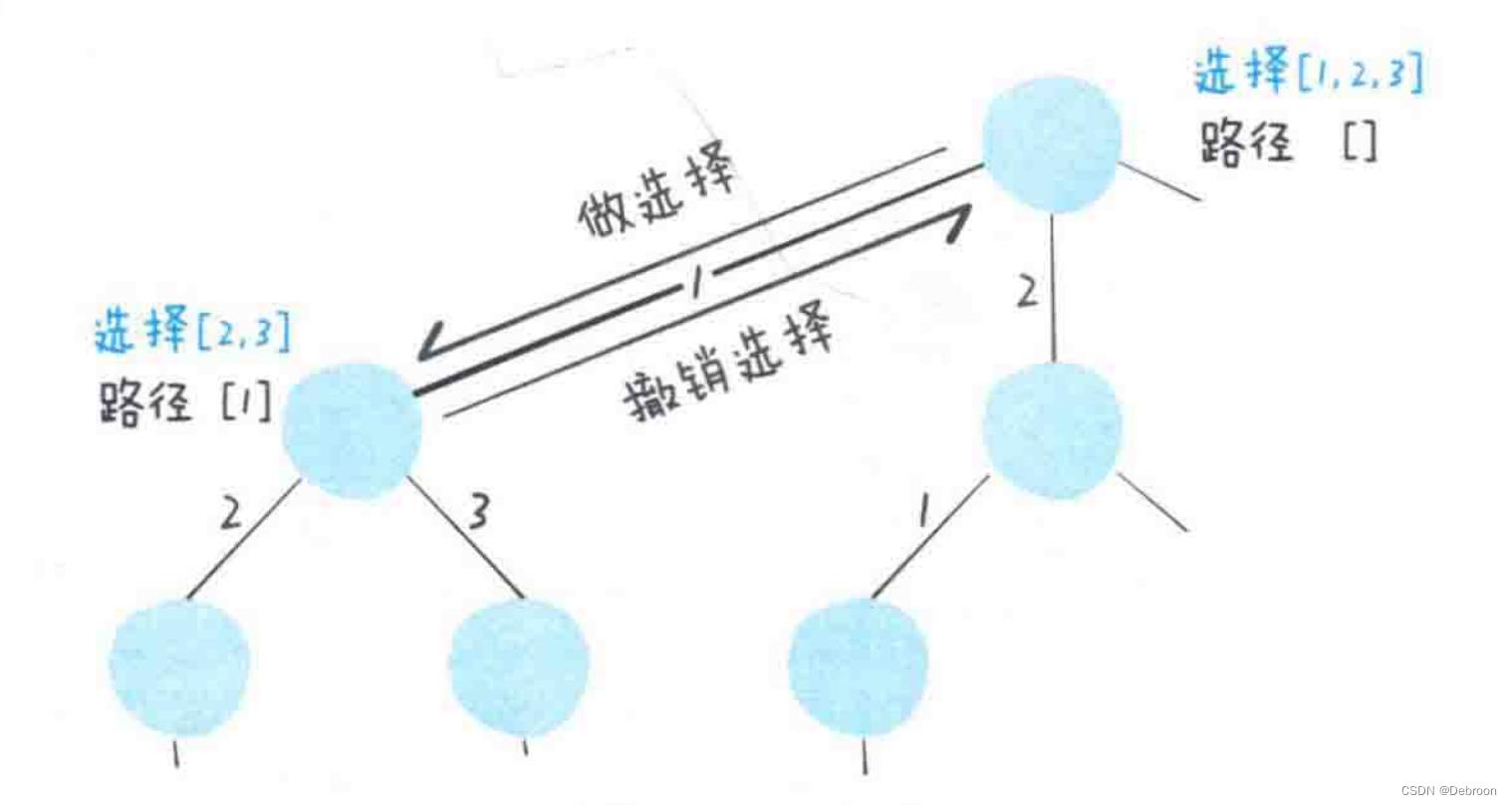
做选择:在进入节点前,从选择列表拿出一个选择,将它放入路径。
撤销选择:在离开节点后,从路径中拿出一个选择,将它恢复到选择列表中。
回溯法采用试错的思想,当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算,再通过其它的可能的分步解答再次尝试寻找问题的答案。
回溯实际上就是“撤回一步”的意思。
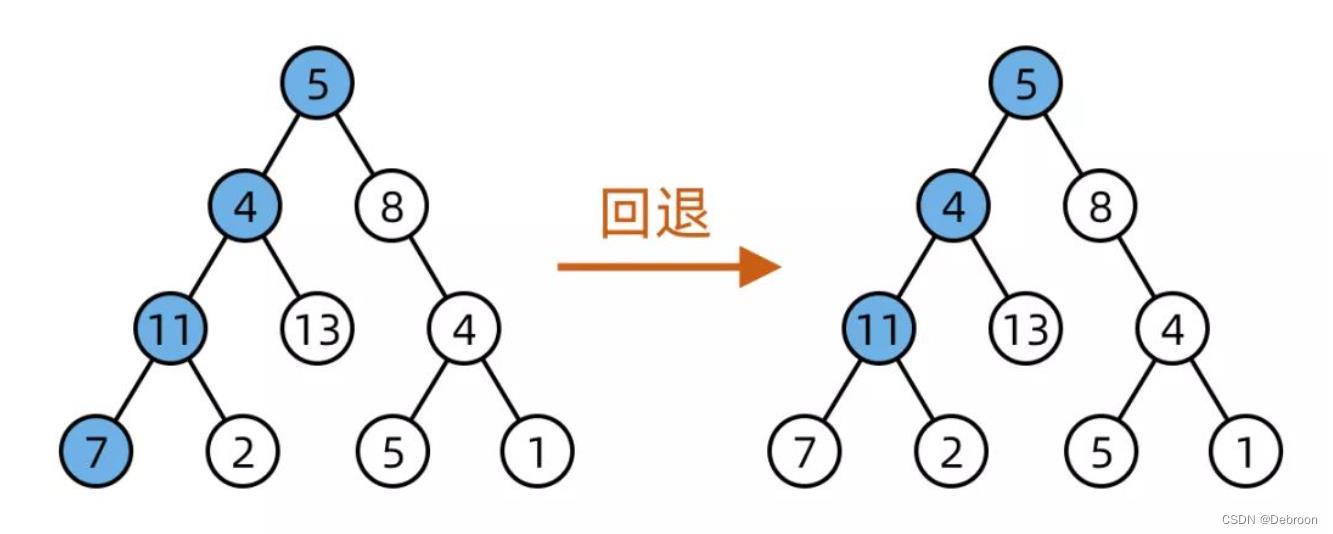
和树的遍历不同的是,回溯算法是在遍历「树枝」,DFS/二叉树遍历是在遍历「节点」。
// DFS/二叉树遍历算法,关注点在节点,DFS 中递归函数返回就是一种回溯
void dfs(TreeNode root)
if (root == null) return;
printf("进入节点 %s", root);
for (TreeNode child : root.children)
dfs(child);
printf("离开节点 %s", root);
// 回溯算法,关注点在树枝,回退过程得用一个栈来维护
void recall(TreeNode root, vector<int> arr[])
if (root == null) return;
for (TreeNode child : root.children)
recall(child); // 不选择第 child 个节点,直接遍历下一个节点
arr.push() // 做选择,push是入栈:在栈顶(数组的尾部)添加指定的元素
recall(child); // 选择第 child 个节点,遍历下一个节点
arr.pop() // 撤销选择,pop是出栈:删除栈顶(数组的尾部)的一个元素,并返回删除的元素。
区别在于位置:
- 回溯算法的「做选择」和「撤销选择」在 for 循环里面
- dfs 的操作在 for 循环外面
区别在于选择:
- 回溯算法,用栈来模拟回退一步,要用 pop 用来回退,营造出不同的选择。
- dfs 的操作,从一个结点退出、递归函数返回就是一种回溯,不用维护。
这是,遍历二叉树模式和回溯模式的区别。
例题:
-
- N 皇后
-
- 括号生成
- 46. 全排列
-
- 组合
-
- 解数独
子问题分解框架
使用场景:可通过子问题/子树的答案推导出原问题的答案。
原问题,分解成当前节点 + 左右子树的子问题。
// 二叉树递归版本
int dp(TreeNode root)
if (root == null) return 0;
// 分解
int left = dp(root.left);
int right = dp(root.right);
// 合并(在把前半部分的最值和后半部分的最值做个比较,相当于求整个大数组的最值)
return 求最值(left, right);
// 多叉树递归版本
int dp(状态1,状态2,···)
for 选择 in 选择列表:
res = 求最值(res, dp(状态1,状态2,···));
return res;
// 递推版
dp[0][0][...] = 0 // 最基础的情况
for 状态1 in 状态1的所有取值: // 一维状态
for 状态2 in 状态2的所有取值: // 二维状态
for ... // N 维状态
dp[状态1][状态2][...] = 求最值(选择1,选择2...) // 状态从哪里来?
因为位置的原因,前序位置的代码只能从函数参数中获取父节点传递来的数据,而后序位置的代码不仅可以获取参数数据,还可以获取到子树通过函数返回值传递回来的数据。
一旦发现问题和子树有关,我们用后序位置 + 给函数设置返回值,可以简化代码。
子问题分解模式和遍历二叉树、回溯模式的区别就在于,利用递归函数的返回值。
例题:
- 105. 从前序与中序遍历序列构造二叉树
-
- 从中序与后序遍历序列构造二叉树
-
- 根据前序和后序遍历构造二叉树
-
- 所有可能的真二叉树
-
- 最大二叉树 II
-
- 删点成林
相邻节点遍历框架
使用场景:在二叉树的前/中/后序遍历时,对相邻结点进行操作。
TreeNode pre; // pre 指向中序遍历的上一个结点
void traverse(TreeNode cur) // cur 指向中序遍历的当前结点
if (cur == null) return;
traverse(cur.left); // 左子树
if (pre != null) // 中序位置做某事
pre = cur; // 维护 pre 指针
traverse(cur.right); // 右子树
链表遍历框架是在链表遍历中维护一个 pre 指针指向前一个结点。
二叉树的相邻节点遍历框架是在,二叉树中序遍历(左、中、右)的基础上,增加了一个 pre 指向中序遍历的上一个结点,并在每次遍历的时候对 pre 和 cur 这一对结点进行操作。
每次对 pre 和 cur 这一对相邻结点进行操作,意味着什么呢?
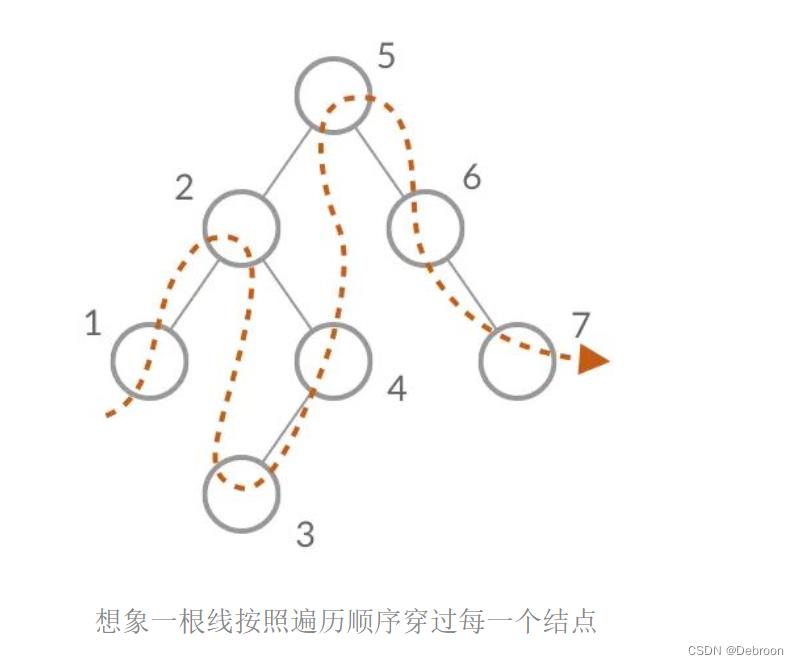
每次遍历时,pre 和 cur 指向这根线上的相邻节点。
例题:
- 98. 验证二叉搜索树:二叉搜索树有一个性质,中序遍历一定是递增的,套用相邻节点框架,判断相邻节点是否递增,得出答案。
- 剑指 Offer 36. 二叉搜索树与双向链表
-
- 二叉树展开为链表
-
- 填充每个节点的下一个右侧节点指针
-
- 填充每个节点的下一个右侧节点指针 II
递归转迭代框架
二叉树前中后序的递归写法没问题,但是迭代就写不出来。
介绍一种写迭代遍历树的实操技巧,统一三种树的遍历方式,这个方法叫做双色标记法。
如果你会了这个技巧,那么你平时练习大可「只用递归」。
我们知道垃圾回收算法中,有一种算法叫颜色标记法。即:
- 用白色表示尚未访问
- 灰色表示尚未完全访问子节点
- 黑色表示子节点全部访问
那么我们可以模仿其思想,使用false/true标记来统一三种遍历。
其核心思想如下:
- 使用不同状态标记节点的状态,新节点为
false,已访问的节点为true。 - 如果遇到的节点为
false,则将其标记为true,然后将其右子节点、自身、左子节点依次入栈。 - 如果遇到的节点为
true,则将节点的值输出。
vector<int> colour_book(TreeNode* root) // 中序遍历版
vector<int> res; // 存放答案的数组
stack<pair<TreeNode*, bool >> stk; // false 是未访问, true 是访问
stk.push( root, false ); // 放入根节点
while (!stk.empty())
TreeNode* node = stk.top().first; // 节点
bool visited = stk.top().second; // 访问状态
stk.pop(); // 弹出节点
if (node == NULL) continue; // 空节点
if (visited == false) // 没有访问
// 中序遍历: 左 根 右,栈先入后出,所以放入顺序:右 根 左
stk.push( node->right, false ); // push是在栈顶添加元素,但孩子节点还没访问
stk.push( node, true ); // 当前节点改为已访问
stk.push( node->left, false );
else // 已经访问了,加入res
res.push_back(node->val); // 将节点值加入答案数组,push_back是在数组末尾添加元素
return res;
false 就表示的是递归中的第一次进入过程,true 则表示递归中的从叶子节点返回的过程。
实现前序、后序遍历,前中后序遍历只需要调整根节点的位置,其他部分是无需做任何变化。
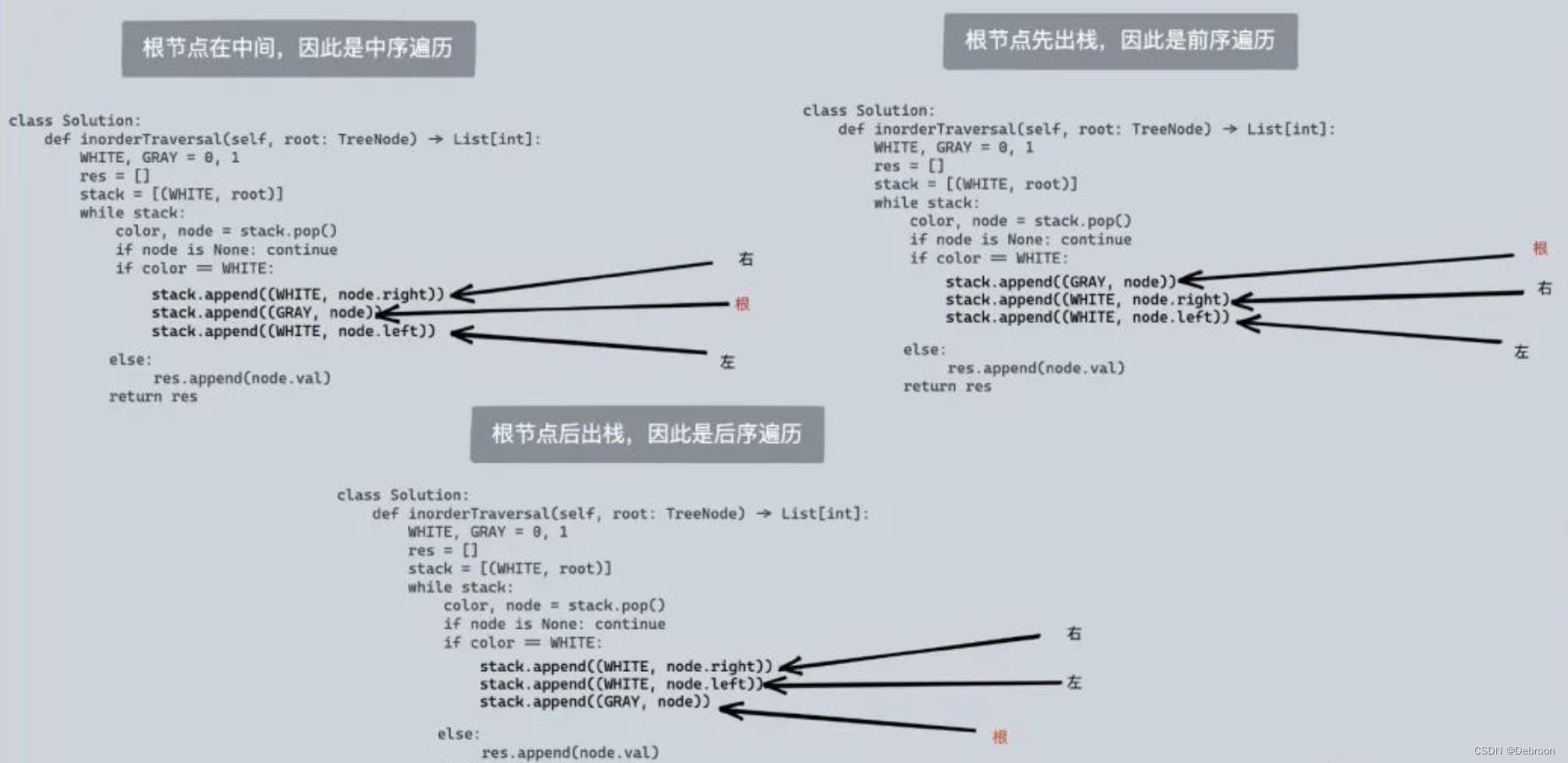
备注:上图的 white 是 false,gray 是 true。
- 中序遍历:右 根 左
- 前序遍历:根 右 左
- 后序遍历:右 左 根
这种写法类似递归的形式,因此便于记忆和书写。
正常写法,把递归改成迭代是繁琐的,需要你画图理解才能写出来,一般面试官才会让你这么写,毕竟递归大家都会写。
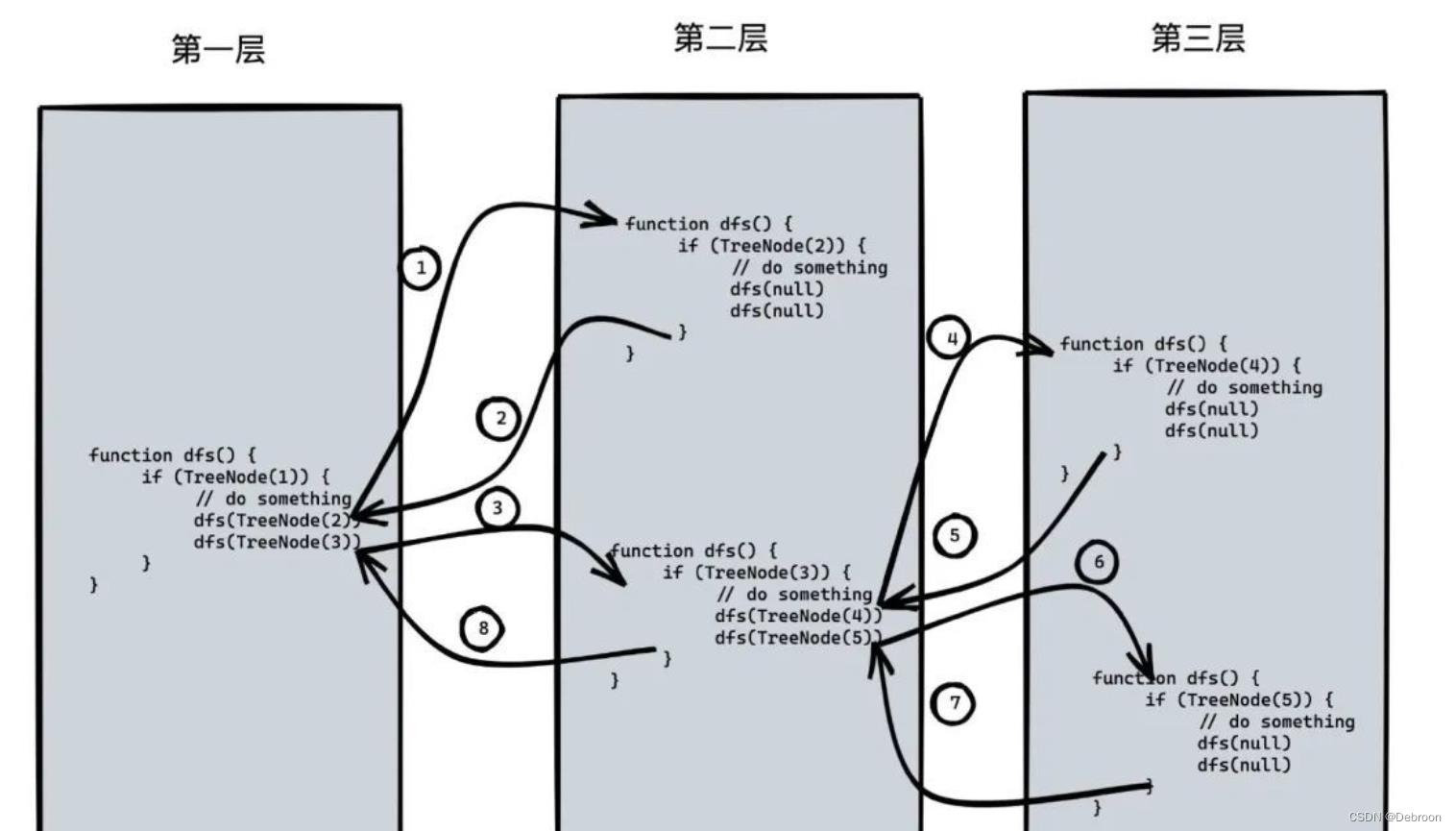
状态标记法的每一个节点都会入栈出栈两次,相比普通的迭代入栈和出栈次数整整加了一倍,这种时间和空间的增加仅仅是常数项的增加。
θ ( n ) 和 θ ( 2 n ) \\theta(n) ~和~ \\theta(2n) θ(n) 和 θ(2n),我们默认是同一量级。
再怎么样,这种写法也比递归的开销小。
例题:
-
递归算法很简单,你可以通过迭代算法完成吗?
以上是关于二叉树和递归框架的主要内容,如果未能解决你的问题,请参考以下文章