神经网络优化 - 学习率
Posted gengyi
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了神经网络优化 - 学习率相关的知识,希望对你有一定的参考价值。
1 学习率的基本定义
学习率learning_rate:每次参数更新的幅度。
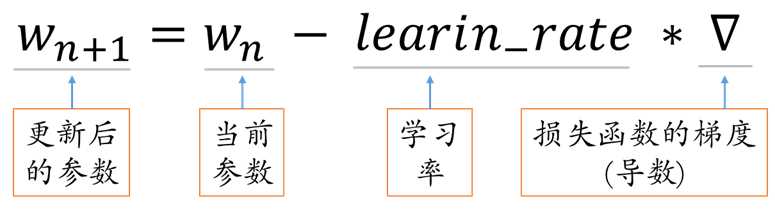
简单示例:
假设损失函数 loss = ( w + 1 )2,则梯度为
![]()
参数 w 初始化为 5 ,学习率为 0.2 ,则
| 运行次数 | 参数w值 | 计算 |
| 1次 | 5 | 5-0.2*(2*5+2) = 2.6 |
| 2次 | 2.6 | 2.6-0.2*(2*2.6+2) = 1.16 |
| 3次 | 1.16 | 1.16-0.2*(2*1.16+2) = 0.296 |
| 4次 | 0.296 |
2 学习率的初步应用
2.1 学习率 0.2 时
# 已知损失函数loss = (w+1)^2,待优化参数W的初值为5 # 求loss最小时对应的W值 # 第一步 引入库,生成数据表 import tensorflow as tf # 第二步 定义前向传播 # 定义待优化参数w初值赋5 w = tf.Variable(tf.constant(5, dtype=tf.float32)) # 第三步 定义损失函数和反向传播 # 定义损失函数loss loss = tf.square(w+1) # 定义反向传播方法,学习率为0.2 train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss) # 第四步 生成会话,训练40轮 with tf.Session() as sess: init_op = tf.global_variables_initializer() sess.run(init_op) for i in range(40): sess.run(train_step) w_val = sess.run(w) loss_val = sess.run(loss) print("After %s steps: w is %f, loss is %f." % (i, w_val, loss_val))
运行
After 0 steps: w is 2.600000, loss is 12.959999. After 1 steps: w is 1.160000, loss is 4.665599. After 2 steps: w is 0.296000, loss is 1.679616. After 3 steps: w is -0.222400, loss is 0.604662. After 4 steps: w is -0.533440, loss is 0.217678. After 5 steps: w is -0.720064, loss is 0.078364. After 6 steps: w is -0.832038, loss is 0.028211. After 7 steps: w is -0.899223, loss is 0.010156. After 8 steps: w is -0.939534, loss is 0.003656. After 9 steps: w is -0.963720, loss is 0.001316. After 10 steps: w is -0.978232, loss is 0.000474. After 11 steps: w is -0.986939, loss is 0.000171. After 12 steps: w is -0.992164, loss is 0.000061. After 13 steps: w is -0.995298, loss is 0.000022. After 14 steps: w is -0.997179, loss is 0.000008. After 15 steps: w is -0.998307, loss is 0.000003. After 16 steps: w is -0.998984, loss is 0.000001. After 17 steps: w is -0.999391, loss is 0.000000. After 18 steps: w is -0.999634, loss is 0.000000. After 19 steps: w is -0.999781, loss is 0.000000. After 20 steps: w is -0.999868, loss is 0.000000. After 21 steps: w is -0.999921, loss is 0.000000. After 22 steps: w is -0.999953, loss is 0.000000. After 23 steps: w is -0.999972, loss is 0.000000. After 24 steps: w is -0.999983, loss is 0.000000. After 25 steps: w is -0.999990, loss is 0.000000. After 26 steps: w is -0.999994, loss is 0.000000. After 27 steps: w is -0.999996, loss is 0.000000. After 28 steps: w is -0.999998, loss is 0.000000. After 29 steps: w is -0.999999, loss is 0.000000. After 30 steps: w is -0.999999, loss is 0.000000. After 31 steps: w is -1.000000, loss is 0.000000. After 32 steps: w is -1.000000, loss is 0.000000. After 33 steps: w is -1.000000, loss is 0.000000. After 34 steps: w is -1.000000, loss is 0.000000. After 35 steps: w is -1.000000, loss is 0.000000. After 36 steps: w is -1.000000, loss is 0.000000. After 37 steps: w is -1.000000, loss is 0.000000. After 38 steps: w is -1.000000, loss is 0.000000. After 39 steps: w is -1.000000, loss is 0.000000.
从运算过程可以得出,待优化参数 w 由原来的初赋值参数 5 最终在 after 31 step 优化成 -1,直到 after 39 step 一直保持 -1。
2.2 学习率为 1 时
# 定义反向传播方法,学习率为 1 train_step = tf.train.GradientDescentOptimizer(1).minimize(loss)
运行
After 0 steps: w is -7.000000, loss is 36.000000. After 1 steps: w is 5.000000, loss is 36.000000. After 2 steps: w is -7.000000, loss is 36.000000. After 3 steps: w is 5.000000, loss is 36.000000. After 4 steps: w is -7.000000, loss is 36.000000. After 5 steps: w is 5.000000, loss is 36.000000. After 6 steps: w is -7.000000, loss is 36.000000. After 7 steps: w is 5.000000, loss is 36.000000. After 8 steps: w is -7.000000, loss is 36.000000. After 9 steps: w is 5.000000, loss is 36.000000. After 10 steps: w is -7.000000, loss is 36.000000. After 11 steps: w is 5.000000, loss is 36.000000. After 12 steps: w is -7.000000, loss is 36.000000. After 13 steps: w is 5.000000, loss is 36.000000. After 14 steps: w is -7.000000, loss is 36.000000. After 15 steps: w is 5.000000, loss is 36.000000. After 16 steps: w is -7.000000, loss is 36.000000. After 17 steps: w is 5.000000, loss is 36.000000. After 18 steps: w is -7.000000, loss is 36.000000. After 19 steps: w is 5.000000, loss is 36.000000. After 20 steps: w is -7.000000, loss is 36.000000. After 21 steps: w is 5.000000, loss is 36.000000. After 22 steps: w is -7.000000, loss is 36.000000. After 23 steps: w is 5.000000, loss is 36.000000. After 24 steps: w is -7.000000, loss is 36.000000. After 25 steps: w is 5.000000, loss is 36.000000. After 26 steps: w is -7.000000, loss is 36.000000. After 27 steps: w is 5.000000, loss is 36.000000. After 28 steps: w is -7.000000, loss is 36.000000. After 29 steps: w is 5.000000, loss is 36.000000. After 30 steps: w is -7.000000, loss is 36.000000. After 31 steps: w is 5.000000, loss is 36.000000. After 32 steps: w is -7.000000, loss is 36.000000. After 33 steps: w is 5.000000, loss is 36.000000. After 34 steps: w is -7.000000, loss is 36.000000. After 35 steps: w is 5.000000, loss is 36.000000. After 36 steps: w is -7.000000, loss is 36.000000. After 37 steps: w is 5.000000, loss is 36.000000. After 38 steps: w is -7.000000, loss is 36.000000. After 39 steps: w is 5.000000, loss is 36.000000.
当学习率过大时,结果并不能收敛,只是在来回震荡,而实际上,有的值还越跳越大。
学习率过大,震荡不收敛。
2.3 学习率为 0.001 时
# 定义反向传播方法,学习率为 1 train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)
运行
After 0 steps: w is 4.988000, loss is 35.856144. After 1 steps: w is 4.976024, loss is 35.712864. After 2 steps: w is 4.964072, loss is 35.570156. After 3 steps: w is 4.952144, loss is 35.428020. After 4 steps: w is 4.940240, loss is 35.286449. After 5 steps: w is 4.928360, loss is 35.145447. After 6 steps: w is 4.916503, loss is 35.005009. After 7 steps: w is 4.904670, loss is 34.865124. After 8 steps: w is 4.892860, loss is 34.725803. After 9 steps: w is 4.881075, loss is 34.587044. After 10 steps: w is 4.869313, loss is 34.448833. After 11 steps: w is 4.857574, loss is 34.311172. After 12 steps: w is 4.845859, loss is 34.174068. After 13 steps: w is 4.834167, loss is 34.037510. After 14 steps: w is 4.822499, loss is 33.901497. After 15 steps: w is 4.810854, loss is 33.766029. After 16 steps: w is 4.799233, loss is 33.631104. After 17 steps: w is 4.787634, loss is 33.496712. After 18 steps: w is 4.776059, loss is 33.362858. After 19 steps: w is 4.764507, loss is 33.229538. After 20 steps: w is 4.752978, loss is 33.096756. After 21 steps: w is 4.741472, loss is 32.964497. After 22 steps: w is 4.729989, loss is 32.832775. After 23 steps: w is 4.718529, loss is 32.701576. After 24 steps: w is 4.707092, loss is 32.570904. After 25 steps: w is 4.695678, loss is 32.440750. After 26 steps: w is 4.684287, loss is 32.311119. After 27 steps: w is 4.672918, loss is 32.182003. After 28 steps: w is 4.661572, loss is 32.053402. After 29 steps: w is 4.650249, loss is 31.925320. After 30 steps: w is 4.638949, loss is 31.797745. After 31 steps: w is 4.627671, loss is 31.670683. After 32 steps: w is 4.616416, loss is 31.544128. After 33 steps: w is 4.605183, loss is 31.418077. After 34 steps: w is 4.593973, loss is 31.292530. After 35 steps: w is 4.582785, loss is 31.167484. After 36 steps: w is 4.571619, loss is 31.042938. After 37 steps: w is 4.560476, loss is 30.918892. After 38 steps: w is 4.549355, loss is 30.795341. After 39 steps: w is 4.538256, loss is 30.672281.
在学习率调整至 0.001 后,w值也收敛,只是变化太慢,在 after 39 step 后才从 5 --> 4.5 ,从第一例可知,最终的优化结果为 -1 , 很显然,当学习率过低时,运行效率非常低。
学习率过小时,收敛速度太慢。
3 指数衰减学习率
3.1 指数衰减学习率数学释义
指数衰减学习率是根据运行的轮数动态调整学习率。
具体多少轮更新一次学习率RATE_STEP = 总样本数 / BATCH_SIZE
将总样本数量分割成 N 个 BATCH_SIZE 参数喂入神经网络训练。每喂入 BATCH_SIZE 数据量循环一轮,当数据集的子集均已喂入神经网络后,调整一次学习率。
一个神经网络训练多少次是设定好的,记为global_step
学习率更新次数 = global_step / RATE_STEP
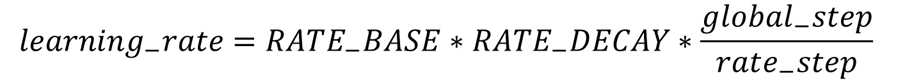
备注:
learning_rate - 学习率更新后的值
RATE_BAST - 学习率基数,学习率初始值
RATE_DECAY - 学习率衰减率,一般值范围( 0, 1 )
global_step - 运行总轮次数
rate_step - 多少轮更新一次学习率
3.2 指数衰减学习率 Tensorflow 代码
global_step= tf.Variable(0, trainable = False)
由于这个变量只为计数,trainable = False 意味该数据不可训练
以上是关于神经网络优化 - 学习率的主要内容,如果未能解决你的问题,请参考以下文章