差分拘束介绍总结与例题

Posted mimiorz

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了差分拘束介绍总结与例题相关的知识，希望对你有一定的参考价值。

差分约束的具体概念：

如果一个系统由n个变量和m个约束条件组成，形成m个形如ai-aj≤k的不等式(i,j∈[1,n],k为常数),则称其为差分约束系统。

例子：

假设有3个数a，b，c
我们知道：

a-b>=2
b-c>=3
a-c>=3

那么：a与c的差值最小为多少？

a比b至少大2，b比c至少大3，那a比c就至少大5。

这很容易理解。

但是如果不等式很多呢？

100个数？1000个数？10000个数……

我们从一开始的例子开始考虑。

我们把这想象成一个图。每个不等式就是一条有向边。
那么：

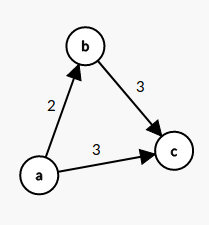
技术分享图片

是不是发现跑一下最长路就可以了？

没错，差分拘束就是用了这个原理。

一般差分拘束问题都可以转化为最短(长)路问题。

问题解的存在性：

1.无解：

比如a-b>=2,b-a>=1,这样就自相矛盾了。

如果连成图，就会发现这是一个负环。

2.无法确定：

比如只给a-b>=2，就无法判断a与c的关系。

连成图后表现为：a与c不连通。

不等式组的转化：

对于题目中的不等式，一般只有转成相同符号才方便处理。

  1. a-b>=t → b-a<=-t
  2. a-b<t → b-a<=t-1
  3. a-b=t → a-b<=t && a-b>=t

根据情况，按上面所说转化。

例题：

1.LUOGU P1250 种树

题目描述

一条街的一边有几座房子。因为环保原因居民想要在路边种些树。路边的地区被分割成块，并被编号成1..N。每个部分为一个单位尺寸大小并最多可种一棵树。每个居民想在门前种些树并指定了三个号码B，E，T。这三个数表示该居民想在B和E之间最少种T棵树。当然，B≤E，居民必须记住在指定区不能种多于区域地块数的树，所以T≤E-B+l。居民们想种树的各自区域可以交叉。你的任务是求出能满足所有要求的最少的树的数量。

写一个程序完成以下工作：

输入输出格式

输入格式：

第一行包含数据N，区域的个数(0<N≤30000)；

第二行包含H，房子的数目(0<H≤5000)；

下面的H行描述居民们的需要：B E T，0<B≤E≤30000，T≤E-B+1。

输出格式：

输出文件只有一行写有树的数目

输入输出样例

输入样例#1：

9
4
1 4 2
4 6 2
8 9 2
3 5 2

输出样例#1：

5

题解：

#include<bits/stdc++.h>
#pragma GCC optimize(3)
namespace ZDY{
    #define res register
    #define ri res int
    #define ll long long
    #define db double
    #define sht short
    #define il inline
    #define MB template <class T>
    #define Fur(i,x,y) for(ri i=x;i<=y;i++)
    #define fur(i,x,y) for(i=x;i<=y;i++)
    #define Fdr(i,x,y) for(ri i=x;i>=y;i--)
    #define clr(x,y) memset(x,y,sizeof(x))
    #define cpy(x,y) memcpy(x,y,sizeof(x))
    #define fl(i,x) for(ri i=head[x],to;to=e[i].to,i;i=e[i].nxt)
    #define inf 2147483630
    #define fin(s) freopen(s".in","r",stdin)
    #define fout(s) freopen(s".out","w",stdin)
    #define l2(n) (ceil(log2(n)))
    #define fast ios::sync_with_stdio(false)
    MB il T ABS(T x){return x>0?x:-x;}
    MB il T MAX(T x,T y){return x>y?x:y;}
    MB il T MIN(T x,T y){return x<y?x:y;}
    MB il T GCD(T x,T y){return y?GCD(y,x%y):x;}
    MB il void SWAP(T x,T y){T t=x;y=t;x=y;}
}using namespace ZDY;using namespace std;
#define N 30010

struct edge{int to,nxt,w;}e[N*2+5010];
int head[N],cnt=0,n,m,d[N];
bool v[N];
struct cmp{bool operator()(int a,int b){return d[a]<d[b];}};
priority_queue<int,vector<int>,cmp>q;
il void add(int x,int y,int w){e[++cnt].to=y;e[cnt].w=w;e[cnt].nxt=head[x];head[x]=cnt;}
il void spfa(){
    int x;
    q.push(0);
    while(!q.empty()){
        x=q.top();q.pop();v[x]=0;
        fl(i,x)
        if(d[x]+e[i].w>d[to]){
            d[to]=d[x]+e[i].w;
            if(!v[to])q.push(to),v[to]=1;
        }
    }
}
int main(){
    fast;
    cin>>n>>m;
    int x,y,w;
    Fur(i,1,m)cin>>x>>y>>w,add(x-1,y,w);
    Fur(i,0,n){
        if(i!=0)add(i-1,i,0),d[i]=-inf;
        if(i!=n)add(i,i-1,-1);
    }
    spfa();
    cout<<d[n];
}

2.LUOGU P1645 序列

题目描述

有一个整数序列，它的每个数各不相同，我们不知道它的长度是多少（即整数个数），但我们知道在某些区间中间至少有多少个整数，用区间（Li,Ri,Ci）来描述，表示这个整数序列中至少有Ci个数来自区间[Li,Ri]，给出若干个这样的区间，问这个整数序列的长度最少能为多少？

输入输出格式

输入格式：

第一行一个整数N，表示区间个数；

接下来N行，每行三个整数（Li,Ri,Ci），描述一个区间。

【数据规模】

N<=1000，0<=Li<=Ri<=1000,1<=Ci<=Ri-Li+1

输出格式：

仅一个数，表示该整数序列的最小长度。

输入输出样例

输入样例#1：

4
4 5 1
6 10 3
7 10 3
5 6 1

输出样例#1：

4

题解：

#include<bits/stdc++.h>
#pragma GCC optimize(3)
namespace ZDY{
    #define res register
    #define ri res int
    #define ll long long
    #define db double
    #define sht short
    #define il inline
    #define MB template <class T>
    #define Fur(i,x,y) for(ri i=x;i<=y;i++)
    #define fur(i,x,y) for(i=x;i<=y;i++)
    #define Fdr(i,x,y) for(ri i=x;i>=y;i--)
    #define clr(x,y) memset(x,y,sizeof(x))
    #define cpy(x,y) memcpy(x,y,sizeof(x))
    #define fl(i,x) for(ri i=head[x],to;to=e[i].to,i;i=e[i].nxt)
    #define inf 2147483630
    #define fin(s) freopen(s".in","r",stdin)
    #define fout(s) freopen(s".out","w",stdin)
    #define l2(n) (ceil(log2(n)))
    #define fast ios::sync_with_stdio(false)
    MB il T ABS(T x){return x>0?x:-x;}
    MB il T MAX(T x,T y){return x>y?x:y;}
    MB il T MIN(T x,T y){return x<y?x:y;}
    MB il T GCD(T x,T y){return y?GCD(y,x%y):x;}
    MB il void SWAP(T x,T y){T t=x;y=t;x=y;}
}using namespace ZDY;using namespace std;
#define N 1011

struct edge{int to,nxt,w;}e[N*3];
int head[N],cnt=0,n=0,m,d[N];
bool v[N];
struct cmp{bool operator()(int a,int b){return d[a]<d[b];}};
priority_queue<int,vector<int>,cmp>q;
il void add(int x,int y,int w){e[++cnt].to=y;e[cnt].w=w;e[cnt].nxt=head[x];head[x]=cnt;}
il void spfa(){
    int x;
    q.push(0);
    while(!q.empty()){
        x=q.top();q.pop();v[x]=0;
        fl(i,x)
        if(d[x]+e[i].w>d[to]){
            d[to]=d[x]+e[i].w;
            if(!v[to])q.push(to),v[to]=1;
        }
    }
}
int main(){
    fast;
    cin>>m;
    int x,y,w;
    Fur(i,1,m)cin>>x>>y>>w,add(x-1,y,w),n=MAX(n,y);
    Fur(i,0,n){
        if(i!=0)add(i-1,i,0),d[i]=-inf;
        if(i!=n)add(i,i-1,-1);
    }
    spfa();
    cout<<d[n];
}

3.[SCOI2011]糖果

题目描述

幼儿园里有N个小朋友，lxhgww老师现在想要给这些小朋友们分配糖果，要求每个小朋友都要分到糖果。但是小朋友们也有嫉妒心，总是会提出一些要求，比如小明不希望小红分到的糖果比他的多，于是在分配糖果的时候，lxhgww需要满足小朋友们的K个要求。幼儿园的糖果总是有限的，lxhgww想知道他至少需要准备多少个糖果，才能使得每个小朋友都能够分到糖果，并且满足小朋友们所有的要求。

输入输出格式

输入格式：

输入的第一行是两个整数N，K。接下来K行，表示这些点需要满足的关系，每行3个数字，X，A，B。如果X=1， 表示第A个小朋友分到的糖果必须和第B个小朋友分到的糖果一样多；如果X=2， 表示第A个小朋友分到的糖果必须少于第B个小朋友分到的糖果；如果X=3， 表示第A个小朋友分到的糖果必须不少于第B个小朋友分到的糖果；如果X=4， 表示第A个小朋友分到的糖果必须多于第B个小朋友分到的糖果；如果X=5， 表示第A个小朋友分到的糖果必须不多于第B个小朋友分到的糖果；

输出格式：

输出一行，表示lxhgww老师至少需要准备的糖果数，如果不能满足小朋友们的所有要求，就输出-1。

输入输出样例

输入样例#1：

5 7
1 1 2
2 3 2
4 4 1
3 4 5
5 4 5
2 3 5
4 5 1

输出样例#1：

11

说明

【数据范围】

对于30%的数据，保证 N<=100

对于100%的数据，保证 N<=100000

对于所有的数据，保证 K<=100000，1<=X<=5，1<=A, B<=N

题解：

#include<bits/stdc++.h>
#pragma GCC optimize(3)
namespace ZDY{
    #define res register
    #define ri res int
    #define ll long long
    #define db double
    #define sht short
    #define il inline
    #define MB template <class T>
    #define Fur(i,x,y) for(ri i=x;i<=y;i++)
    #define fur(i,x,y) for(i=x;i<=y;i++)
    #define Fdr(i,x,y) for(ri i=x;i>=y;i--)
    #define clr(x,y) memset(x,y,sizeof(x))
    #define cpy(x,y) memcpy(x,y,sizeof(x))
    #define fl(i,x) for(ri i=head[x],to;to=e[i].to,i;i=e[i].nxt)
    #define inf 2147483630
    #define fin(s) freopen(s".in","r",stdin)
    #define fout(s) freopen(s".out","w",stdin)
    #define l2(n) (ceil(log2(n)))
    #define fast ios::sync_with_stdio(false)
    MB il T ABS(T x){return x>0?x:-x;}
    MB il T MAX(T x,T y){return x>y?x:y;}
    MB il T MIN(T x,T y){return x<y?x:y;}
    MB il T GCD(T x,T y){return y?GCD(y,x%y):x;}
    MB il void SWAP(T x,T y){T t=x;y=t;x=y;}
}using namespace ZDY;using namespace std;
#define N 100010

struct edge{int to,nxt,w;}e[N*3];
int head[N],cnt=0,n=0,m,d[N],t[N];
bool v[N];
struct cmp{bool operator()(int a,int b){return d[a]<d[b];}};
priority_queue<int,vector<int>,cmp>q;
il void add(int x,int y,int w){e[++cnt].to=y;e[cnt].w=w;e[cnt].nxt=head[x];head[x]=cnt;}
il void spfa(){
    int x;
    q.push(0);
    while(!q.empty()){
        x=q.top();q.pop();v[x]=0;if(++t[x]>n){cout<<-1<<endl;exit(0);}
        fl(i,x)
        if(d[x]+e[i].w>d[to]){
            d[to]=d[x]+e[i].w;
            if(!v[to])q.push(to),v[to]=1;
        }
    }
}
int main(){
    fast;
    cin>>n>>m;
    int p,x,y;
    ll ans=0;
    Fur(i,1,m){
        cin>>p>>x>>y;
        if(p==1)add(x,y,0),add(y,x,0);
        if(p==2)add(x,y,1);
        if(p==3)add(y,x,0);
        if(p==4)add(y,x,1);
        if(p==5)add(x,y,0);
    }
    Fur(i,1,n)add(0,i,1);
    spfa();
    Fur(i,1,n)ans+=d[i];
    cout<<ans<<endl;
}

以上是关于差分拘束介绍总结与例题的主要内容，如果未能解决你的问题，请参考以下文章

浅谈差分约束系统

算法基础| 差分算法及模板详解

算法基础：差分算法及模板应用

求基于OpenCV的三帧差分算法代码

差分例题-增减序列

浅析树状数组