Lloyd’s 算法 和 K-Means算法

Posted 2021-01-15 zhxuxu

在讲Lloyd’s 算法之前先介绍Voronoi图

在数学中，Voronoi图是基于到平面的特定子集中的点的距离将平面划分成区域。预先指定一组点（称为种子，站点或生成器），并且对于每个种子，存在相应的区域，该区域由更接近该种子的所有点组成，而不是任何其他点。这些区域称为Voronoi细胞。

在最简单的情况下，如图所示，我们在欧几里德平面上给出了一组有限的点{p1，...，pn}。在这种情况下每个站点pk只是一个点，其相应的Voronoi单元Rk由欧几里德平面中的每个点组成，其与pk的距离小于或等于其与任何其他pk的距离。每个这样的单元是从半空间的交点获得的，因此它是凸多边形。 Voronoi图的边界是平面中与两个最近的站点等距的所有点。 Voronoi顶点（节点）是与三个（或更多）站点等距的点。

Lloyd’s algorithm 过程：

（1）首先在数据集中随机选定k个初始点

（2） 计算k个站点的Voronoi图。

（3）整合Voronoi图的每个单元格，并计算质心。

（4）然后将每个站点（k）移动到其Voronoi单元的质心。

如下图迭代过程

           

 

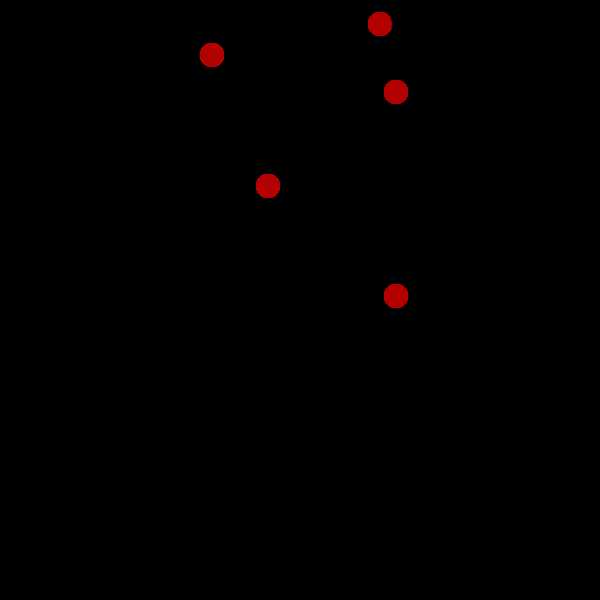
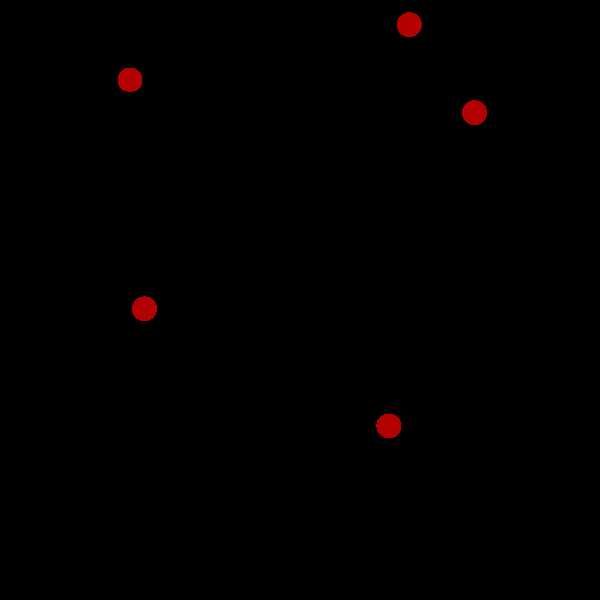
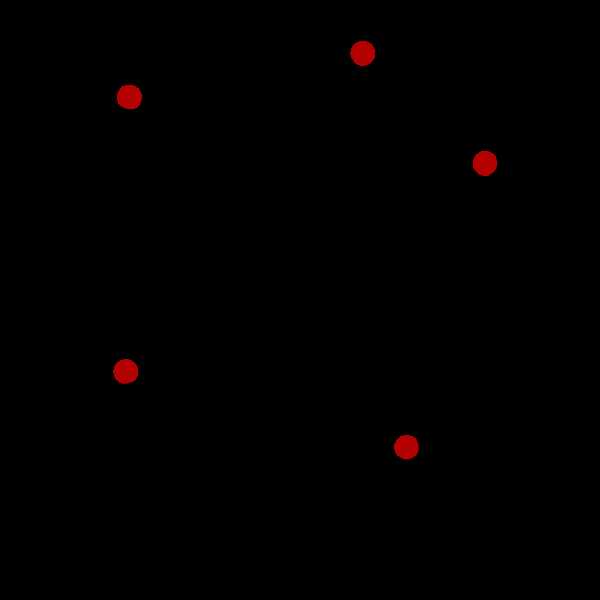
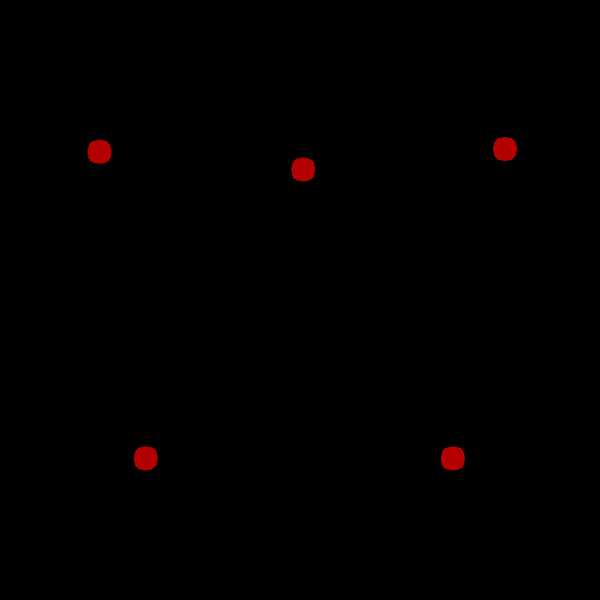
K-Means算法过程：

（1）随机初始化k个聚类中心的位置

（2）计算每一个点到聚类中心的距离，选取最小值分配给k(i)

（3）移动聚类中心（其实就是对所属它的样本点求平均值，就是它移动是位置）

（4）重复（2），（3）直到损失函数（也就是所有样本点到其所归属的样本中心的距离的和最小）

最后整体分类格局会变得稳定。

如下图

 

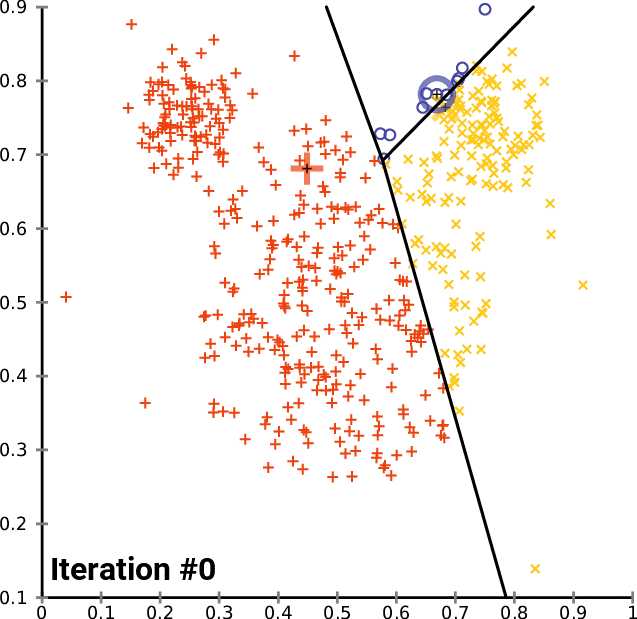
通过对比，可以发现这两个算法之间有许多相似之处，都是迭代的寻找聚族中心的位置。

然而，Lloyd’s算法与k均值聚类的不同之处在于，Lloyd’s的输入是一个连续的几何区域，而不是一组离散的点。

因此，当重新划分输入时，劳埃德算法使用Voronoi图而不是像k-means算法那样简单地确定每个有限点集的最近中心。