粒子群算法

Posted 2021-01-15 kexinxin

粒子群算法

粒子群算法是在1995年由Eberhart博士和Kennedy博士一起提出的，它源于对鸟群捕食行为的研究。它的基本核心是利用群体中的个体对信息的共享从而使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得问题的最优解。设想这么一个场景：一群鸟进行觅食，而远处有一片玉米地，所有的鸟都不知道玉米地到底在哪里，但是它们知道自己当前的位置距离玉米地有多远。那么找到玉米地的最佳策略，也是最简单有效的策略就是搜寻目前距离玉米地最近的鸟群的周围区域。

    在PSO中，每个优化问题的解都是搜索空间中的一只鸟，称之为"粒子"，而问题的最优解就对应于鸟群中寻找的"玉米地"。所有的粒子都具有一个位置向量（粒子在解空间的位置）和速度向量（决定下次飞行的方向和速度），并可以根据目标函数来计算当前的所在位置的适应值（fitness value）,可以将其理解为距离"玉米地"的距离。在每次的迭代中，种群中的例子除了根据自身的经验（历史位置）进行学习以外，还可以根据种群中最优粒子的"经验"来学习，从而确定下一次迭代时需要如何调整和改变飞行的方向和速度。就这样逐步迭代，最终整个种群的例子就会逐步趋于最优解。

上面的解释可能还比较抽象，下面通过一个简单的例子来进行说明

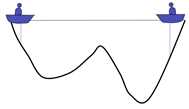
在一个湖中有两个人他们之间可以通信，并且可以探测到自己所在位置的最低点。初始位置如上图所示，由于右边比较深，因此左边的人会往右边移动一下小船。

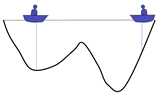
现在左边比较深，因此右边的人会往左边移动一下小船

 

一直重复该过程，最后两个小船会相遇

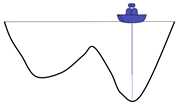
得到一个局部的最优解

 

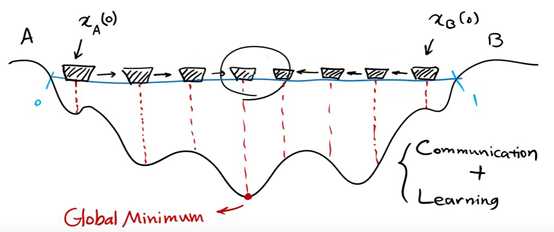
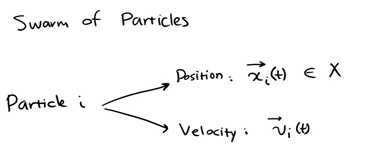
将每个个体表示为粒子。每个个体在某一时刻的位置表示为，x(t),方向表示为v(t)

 

 

 

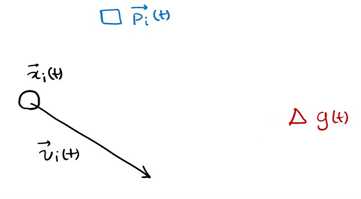
p（t）为在t时刻x个体的自己的最优解，g(t)为在t时刻所有个体的最优解，v(t)为个体在t时刻的方向，x(t)为个体在t时刻的位置

 

 

 

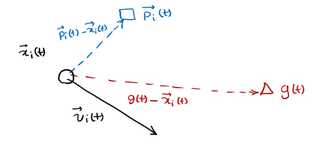
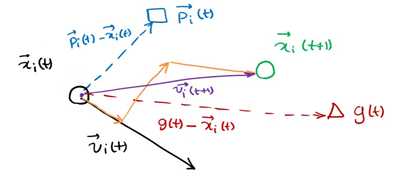
下一个位置为上图所示由x,p,g共同决定了

 

 

 

种群中的粒子通过不断地向自身和种群的历史信息进行学习，从而可以找到问题的最优解。

但是，在后续的研究中表表明，上述原始的公式中存在一个问题：公式中V的更新太具有随机性，从而使整个PSO算法的全局优化能力很强，但是局部搜索能力较差。而实际上，我们需要在算法迭代初期PSO有着较强的全局优化能力，而在算法的后期，整个种群应该具有更强的局部搜索能力。所以根据上述的弊端，shi和Eberhart通过引入惯性权重修改了公式，从而提出了PSO的惯性权重模型：

 

每一个向量的分量表示如下

 

 

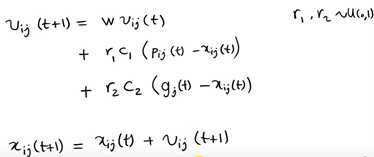
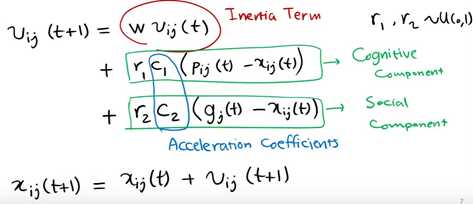
其中w称为是PSO的惯性权重，它的取值介于【0,1】区间，一般应用中均采用自适应的取值方法，即一开始令w=0.9，使得PSO全局优化能力较强，随着迭代的深入，参数w进行递减，从而使的PSO具有较强的局部优化能力，当迭代结束时，w=0.1。参数c1和c2称为学习因子，一般设置为1,4961；而r1和r2为介于[0,1]之间的随机概率值。

整个粒子群优化算法的算法框架如下：

step1种群初始化，可以进行随机初始化或者根据被优化的问题设计特定的初始化方法，然后计算个体的适应值，从而选择出个体的局部最优位置向量和种群的全局最优位置向量。

step2 迭代设置：设置迭代次数，并令当前迭代次数为1

step3 速度更新：更新每个个体的速度向量

step4 位置更新：更新每个个体的位置向量

step5 局部位置和全局位置向量更新：更新每个个体的局部最优解和种群的全局最优解

step6 终止条件判断：判断迭代次数时都达到最大迭代次数，如果满足，输出全局最优解，否则继续进行迭代，跳转至step 3。

　　对于粒子群优化算法的运用，主要是对速度和位置向量迭代算子的设计。迭代算子是否有效将决定整个PSO算法性能的优劣，所以如何设计PSO的迭代算子是PSO算法应用的研究重点和难点。

4. 对粒子群优化算法中惯性权重的认识

参数w被称之为是惯性权重，顾名思义w实际反映了粒子过去的运动状态对当前行为的影响，就像是我们物理中提到的惯性。如果w<<1，从前的运动状态很少能影响当前的行为，粒子的速度会很快的改变；相反，w较大，虽然会有很大的搜索空间，但是粒子很难改变其运动方向，很难向较优位置收敛，由于算法速度的因素，在实际运用中很少这样设置。也就是说，较高的w设置促进全局搜索，较低的w设置促进快速的局部搜索。

 

  1 function z = Sphere(x)
  2     z = sum(x.^2);
  3 end
  4 
  5 
  6 
  7 function out = PSO(problem, params)
  8     %% Problem Definiton
  9     CostFunction = problem.CostFunction;  % Cost Function
 10     nVar = problem.nVar;        % Number of Unknown (Decision) Variables
 11     VarSize = [1 nVar];         % Matrix Size of Decision Variables
 12     VarMin = problem.VarMin;    % Lower Bound of Decision Variables
 13     VarMax = problem.VarMax;    % Upper Bound of Decision Variables
 14     %% Parameters of PSO
 15     MaxIt = params.MaxIt;   % Maximum Number of Iterations
 16     nPop = params.nPop;     % Population Size (Swarm Size)
 17     w = params.w;           % Intertia Coefficient
 18     wdamp = params.wdamp;   % Damping Ratio of Inertia Coefficient
 19     c1 = params.c1;         % Personal Acceleration Coefficient
 20     c2 = params.c2;         % Social Acceleration Coefficient
 21     % The Flag for Showing Iteration Information
 22     ShowIterInfo = params.ShowIterInfo;    
 23     MaxVelocity = 0.2*(VarMax-VarMin);
 24     MinVelocity = -MaxVelocity;
 25     %% Initialization
 26     % The Particle Template
 27     empty_particle.Position = [];
 28     empty_particle.Velocity = [];
 29     empty_particle.Cost = [];
 30     empty_particle.Best.Position = [];
 31     empty_particle.Best.Cost = [];
 32     % Create Population Array
 33     particle = repmat(empty_particle, nPop, 1);
 34     % Initialize Global Best
 35     GlobalBest.Cost = inf;
 36     % Initialize Population Members
 37     for i=1:nPop
 38         % Generate Random Solution
 39         particle(i).Position = unifrnd(VarMin, VarMax, VarSize);
 40         % Initialize Velocity
 41         particle(i).Velocity = zeros(VarSize);
 42         % Evaluation
 43         particle(i).Cost = CostFunction(particle(i).Position);
 44         % Update the Personal Best
 45         particle(i).Best.Position = particle(i).Position;
 46         particle(i).Best.Cost = particle(i).Cost;
 47         % Update Global Best
 48         if particle(i).Best.Cost < GlobalBest.Cost
 49             GlobalBest = particle(i).Best;
 50         end
 51     end
 52     % Array to Hold Best Cost Value on Each Iteration
 53     BestCosts = zeros(MaxIt, 1);
 54     %% Main Loop of PSO
 55     for it=1:MaxIt
 56         for i=1:nPop
 57             % Update Velocity
 58             particle(i).Velocity = w*particle(i).Velocity ...
 59                 + c1*rand(VarSize).*(particle(i).Best.Position - particle(i).Position) ...
 60                 + c2*rand(VarSize).*(GlobalBest.Position - particle(i).Position);
 61             % Apply Velocity Limits
 62             particle(i).Velocity = max(particle(i).Velocity, MinVelocity);
 63             particle(i).Velocity = min(particle(i).Velocity, MaxVelocity);
 64           
 65             % Update Position
 66             particle(i).Position = particle(i).Position + particle(i).Velocity;
 67             % Apply Lower and Upper Bound Limits
 68             particle(i).Position = max(particle(i).Position, VarMin);
 69             particle(i).Position = min(particle(i).Position, VarMax);
 70             % Evaluation
 71             particle(i).Cost = CostFunction(particle(i).Position);
 72             % Update Personal Best
 73             if particle(i).Cost < particle(i).Best.Cost
 74                 particle(i).Best.Position = particle(i).Position;
 75                 particle(i).Best.Cost = particle(i).Cost;
 76                 % Update Global Best
 77                 if particle(i).Best.Cost < GlobalBest.Cost
 78                     GlobalBest = particle(i).Best;
 79                 end            
 80             end
 81         end
 82         % Store the Best Cost Value
 83         BestCosts(it) = GlobalBest.Cost;
 84         % Display Iteration Information
 85         if ShowIterInfo
 86             disp([‘Iteration ‘ num2str(it) ‘: Best Cost = ‘ num2str(BestCosts(it))]);
 87         end
 88         % Damping Inertia Coefficient
 89         w = w * wdamp;
 90     end
 91     
 92     out.pop = particle;
 93     out.BestSol = GlobalBest;
 94     out.BestCosts = BestCosts;
 95     
 96 end
 97 
 98 
 99 %% Problem Definiton
100 problem.CostFunction = @(x) Sphere(x);  % Cost Function
101 problem.nVar = 5;       % Number of Unknown (Decision) Variables
102 problem.VarMin =  -10;  % Lower Bound of Decision Variables
103 problem.VarMax =  10;   % Upper Bound of Decision Variables
104  
105 %% Parameters of PSO
106 params.MaxIt = 1000;        % Maximum Number of Iterations
107 params.nPop = 50;           % Population Size (Swarm Size)
108 params.w = 1;               % Intertia Coefficient
109 params.wdamp = 0.99;        % Damping Ratio of Inertia Coefficient
110 params.c1 = 2;              % Personal Acceleration Coefficient
111 params.c2 = 2;              % Social Acceleration Coefficient
112 params.ShowIterInfo = true; % Flag for Showing Iteration Informatin
113  
114 %% Calling PSO
115 out = PSO(problem, params);
116  
117 BestSol = out.BestSol;
118 BestCosts = out.BestCosts;
119  
120 %% Results
121 figure;
122 % plot(BestCosts, ‘LineWidth‘, 2);
123 semilogy(BestCosts, ‘LineWidth‘, 2);
124 xlabel(‘Iteration‘);
125 ylabel(‘Best Cost‘);
126 grid on;

 

粒子群优化

引入收敛因子，不要惯性权重

Clerc引入收敛因子（contriction factor）保证收敛性

与使用惯性权重的PSO算法相比，使用收敛因子的PSO有更快的收敛速度。其实只要恰当的选取,两种算法是一样的。因此使用收敛因子的PSO可以看作使用惯性权重PSO的特例。恰当的选取算法的参数值可以改善算法的性能。