在2017年末,Face++发了一篇论文ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices讨论了一个极有效率且可以运行在手机等移动设备上的网络结构——ShuffleNet。这个英文名我更愿意翻译成“重组通道网络”,ShuffleNet通过分组卷积与\\(1 \\times 1\\)的卷积核来降低计算量,通过重组通道来丰富各个通道的信息。这个论文的mxnet源码的开源地址为:MXShuffleNet。
分组卷积与核大小对计算量的影响
论文说中到“We propose using pointwise group convolutions to reduce computation complexity of 1 × 1 convolutions”,那么为什么用分组卷积与小的卷积核会减少计算的复杂度呢?先来看看卷积在编程中是如何实现的,Caffe与mxnet的CPU版本都是用差不多的方法实现的,但Caffe的计算代码会更加简洁。
不分组且只有一个样本
在不分组与输入的样本量为1(batch_size=1)的条件下,输出一个通道上的一个点是卷积核会与所有的通道卷积之积,如图1所示:
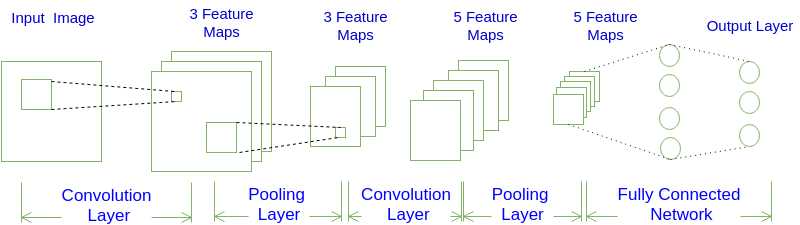
在Caffe的计算方法中,先要将输入张量为\\(n \\times C_{in} \\times H_{in} \\times W_{in}\\)(n是batch_size)转化为一个$ \\left(C_{in} \\times H_k \\times H_w\\right) \\times \\left(H_{in} \\times W_{in}\\right)\\(的矩阵,这个过程叫**im2col**。最后得到的输出张量为\\)n \\times C_{out} \\times H_{in} \\times W_{in}$。
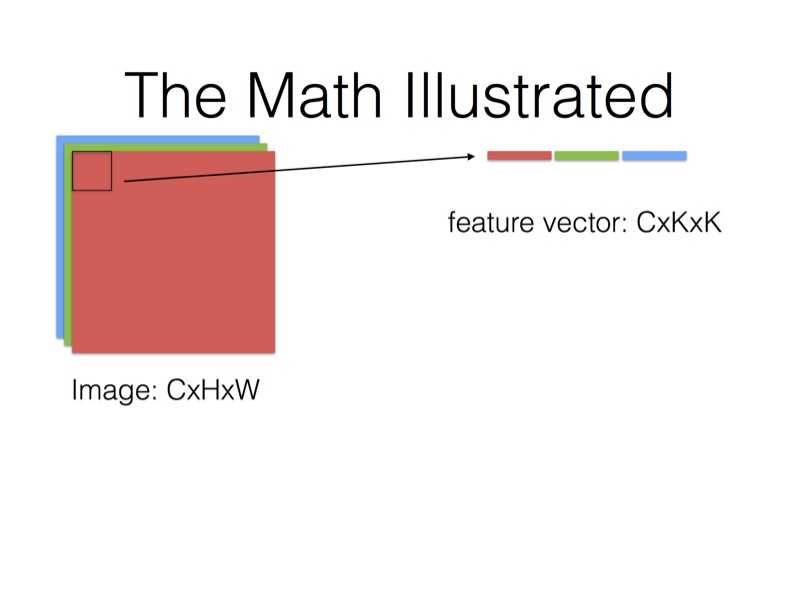
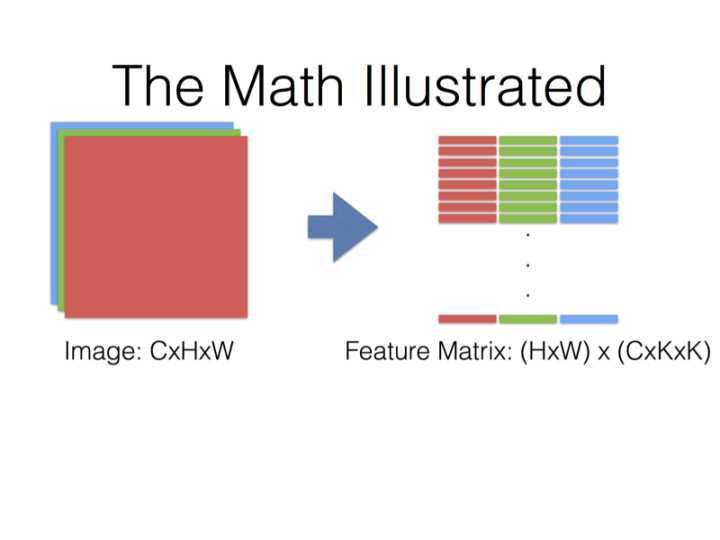
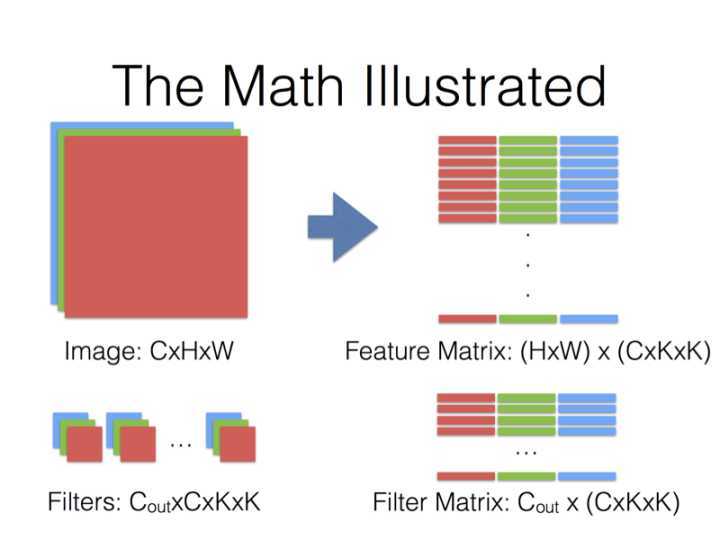
得到的两个矩阵Feature与Filter相乘得到输出矩阵Output,再Reshape成\\(C_{out} \\times C_{in} \\times H_k \\times W_k\\)张量:
\\[
Filter_{C_{out} \\times \\left( C_{in} \\times K_h \\times K_w \\right)} \\times Feature_{\\left(C_{in} \\times H_k \\times H_w\\right) \\times \\left(H_{out} \\times W_{out}\\right)} = Output_{C_{out} \\times (H_{out} \\times W_{out})} \\tag{1.1}
\\]
现在的计算技术中,对方长度为\\(n\\)的方阵,计算量能从\\(n^3\\)代码到\\(n^{2.376}\\),最小的复杂度现在仍然未知,本文为了方便计算量就以\\(n^3\\)为基准。所以式(1.1)的矩阵计算最普通的计算量\\(Computation\\)是:
\\[
Computation=C_{out} \\times H_{out} \\times W_{out} \\times \\left( C_{in} \\times K_h \\times K_w \\right)^2 \\tag{1.2}
\\]
从式(1.2)中可以看出来,卷积核的大小对计算量影响是很大的,\\(3 \\times 3\\)的卷积核比\\(1 \\times 1\\)的计算量要大\\(3^4=81\\)倍。
分组且只有一个样本
什么叫做分组,就是将输入与输出的通道分成几组,比如输出与输入的通道数都是4个且分成2组,那第1、2通道的输出只使用第1、2通道的输入,同样那第3、4通道的输出只使用第1、2通道的输入。也就是说,不同组的输出与输入没有关系了,减少联系必然会使计算量减小,但同时也会导致信息的丢失。
当分成g组后,一层参数量的大小由\\(Filter_{C_{out} \\times \\left( C_{in} \\times K_h \\times K_w \\right)}\\)变成\\(Filter_{C_{out} \\times \\left( C_{in} \\times K_h \\times K_w / g \\right)}\\)。Feature Matrix的大小虽然没发生变化,但是每一组的使用量是原来的$1/g,Filter也只用到所有参数的\\(1/g\\)\\(。然后再循环计算\\)g$次(同时FeatureMatrix与FilterMatrix要有地址偏移),那么计算公式与计算量的大小为:
\\[
Filter_{C_{out}/g \\times \\left( C_{in} \\times K_h \\times K_w /g \\right)} \\times Feature_{\\left(C_{in} \\times H_k \\times H_w /g\\right) \\times \\left(H_{out} \\times W_{out}\\right)} = Output_{C_{out}/g \\times (H_{out} \\times W_{out})} \\tag{1.3}
\\]
\\[
Computation=C_{out} \\times H_{out} \\times W_{out} \\times \\left( C_{in} \\times K_h \\times K_w /g \\right)^2 \\tag{1.4}
\\]
所以,分成\\(g\\)组可以使参数量变成原来的\\(1/g\\),计算量是原来的\\(1/g^2\\)。
多个样本输入
为了节省内存,多个样本输入的时候,上述的所有过程都不会改变,而是每一个样本都运行一次上述的过程。
以上只是最简单、粗略的分析,实际上计算效率的提升并不会有上述这么多,一方面因为im2col会消耗与矩阵运算差不多的时间,另一方面因为现代的blas库优化了矩阵运算,复杂度并没有上述分析的那么多,还有计算过程for循环是比较耗时的指令,即使用openmp也不能优化卷积的计算过程。
交换通道(Shuffle Channels)
在上面我提到过,分组会导致信息的丢失,那么有没有办法来解决这个问题呢?这个论文给出的方法就是交换通道,因为在同一组中不同的通道蕴含的信息可能是相同的,如果在不同的组之后交换一些通道,那么就能交换信息,使得各个组的信息更丰富,能提取到的特征自然就更多,这样是有利于得到更好的结果。
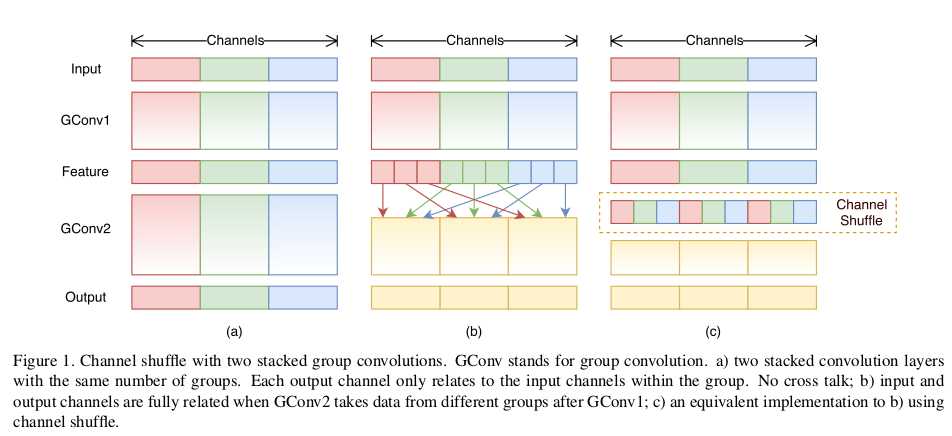
ShuffleUnit
ShuffleUnit的设计参考了ResNet,总有两个基本单元,两人个基本单元功能不一样,将他们组合起来就可以得到ShuffleNet。这样的设计可以在增加网络的深度(比mobilenet深约一倍)的同时,减少参数总量与计算量(本人运行Cifar10时,速度大约是molibenet的10倍)。
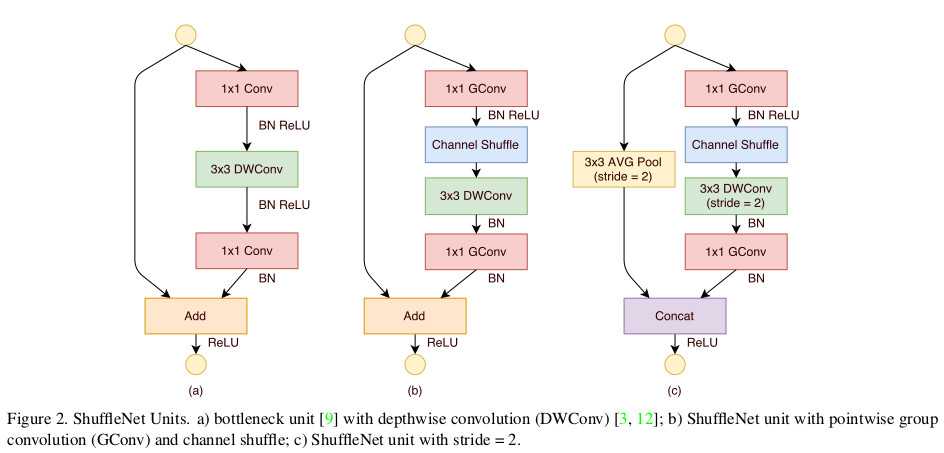
源码解读
def combine(residual, data, combine):
if combine == 'add':
return residual + data
elif combine == 'concat':
return mx.sym.concat(residual, data, dim=1)
return Noneadd是代表图6中的单元b),concat是代表图6中的单元c)。
def channel_shuffle(data, groups):
data = mx.sym.reshape(data, shape=(0, -4, groups, -1, -2))
data = mx.sym.swapaxes(data, 1, 2)
data = mx.sym.reshape(data, shape=(0, -3, -2))
return data这个函数就是交换通道的函数,函数的第一行data = mx.sym.reshape(data, shape=(0, -4, groups, -1, -2))是将输入为\\(n \\times C_{in} \\times H_{in} \\times W_{in}\\)reshape成\\(n \\times (C_{in}/g) \\times g\\times H_{in} \\times W_{in}\\),要注意的是mxnet中reshape不会改变张量在内存中的排列顺序。至于要mxnet中的0,-1,-2,-3,-4的具体意义可以这样看到:
import mxnet as mx
print(help(mx.sym.reshape))可以看到输出以下(只提取出一小部分,其余的可用上述方法查看),这里有各个参数的具体意义:
- ``0`` copy this dimension from the input to the output shape.
- ``-1`` infers the dimension of the output shape by using the remainder of the input dimensions
- ``-2`` copy all/remainder of the input dimensions to the output shape.
- ``-3`` use the product of two consecutive dimensions of the input shape as the output dimension.
- ``-4`` split one dimension of the input into two dimensions passed subsequent to -4 in shape (can contain -1).
函数的第二行是交换第一与第二个维度,那么现在这个symbol的符号的shape就变成了\\(n \\times g \\times (C_{in}/g) \\times H_{in} \\times W_{in}\\)。这里的第零个维度是\\(n\\)。要注意的是交换维度改变了张量在内存中的排列顺序,改变了内存中的顺序实现上就是完成了图5c)中的Channel Shuffle操作,不同的颜色代码数据在原来内存中的位置。
函数的最后一行合并了第一与第二个维度,输出的张量与输入的张量shape都是\\(n \\times C_{in} \\times H_{in} \\times W_{in}\\)。
def shuffleUnit(residual, in_channels, out_channels, combine_type, groups=3, grouped_conv=True):
if combine_type == 'add':
DWConv_stride = 1
elif combine_type == 'concat':
DWConv_stride = 2
out_channels -= in_channels
first_groups = groups if grouped_conv else 1
bottleneck_channels = out_channels // 4
data = mx.sym.Convolution(data=residual, num_filter=bottleneck_channels,
kernel=(1, 1), stride=(1, 1), num_group=first_groups)
data = mx.sym.BatchNorm(data=data)
data = mx.sym.Activation(data=data, act_type='relu')
data = channel_shuffle(data, groups)
data = mx.sym.Convolution(data=data, num_filter=bottleneck_channels, kernel=(3, 3),
pad=(1, 1), stride=(DWConv_stride, DWConv_stride), num_group=groups)
data = mx.sym.BatchNorm(data=data)
data = mx.sym.Convolution(data=data, num_filter=out_channels,
kernel=(1, 1), stride=(1, 1), num_group=groups)
data = mx.sym.BatchNorm(data=data)
if combine_type == 'concat':
residual = mx.sym.Pooling(data=residual, kernel=(3, 3), pool_type='avg',
stride=(2, 2), pad=(1, 1))
data = combine(residual, data, combine_type)
return dataShuffleUnit这个函数实现上是实现图6的b)与c),add对应成b),comcat对应于c)。
def make_stage(data, stage, groups=3):
stage_repeats = [3, 7, 3]
grouped_conv = stage > 2
if groups == 1:
out_channels = [-1, 24, 144, 288, 567]
elif groups == 2:
out_channels = [-1, 24, 200, 400, 800]
elif groups == 3:
out_channels = [-1, 24, 240, 480, 960]
elif groups == 4:
out_channels = [-1, 24, 272, 544, 1088]
elif groups == 8:
out_channels = [-1, 24, 384, 768, 1536]
data = shuffleUnit(data, out_channels[stage - 1], out_channels[stage],
'concat', groups, grouped_conv)
for i in range(stage_repeats[stage - 2]):
data = shuffleUnit(data, out_channels[stage], out_channels[stage],
'add', groups, True)
return data
def get_shufflenet(num_classes=10):
data = mx.sym.var('data')
data = mx.sym.Convolution(data=data, num_filter=24,
kernel=(3, 3), stride=(2, 2), pad=(1, 1))
data = mx.sym.Pooling(data=data, kernel=(3, 3), pool_type='max',
stride=(2, 2), pad=(1, 1))
data = make_stage(data, 2)
data = make_stage(data, 3)
data = make_stage(data, 4)
data = mx.sym.Pooling(data=data, kernel=(1, 1), global_pool=True, pool_type='avg')
data = mx.sym.flatten(data=data)
data = mx.sym.FullyConnected(data=data, num_hidden=num_classes)
out = mx.sym.SoftmaxOutput(data=data, name='softmax')
return out这两个函数可以直接得到作者在论文中的表:
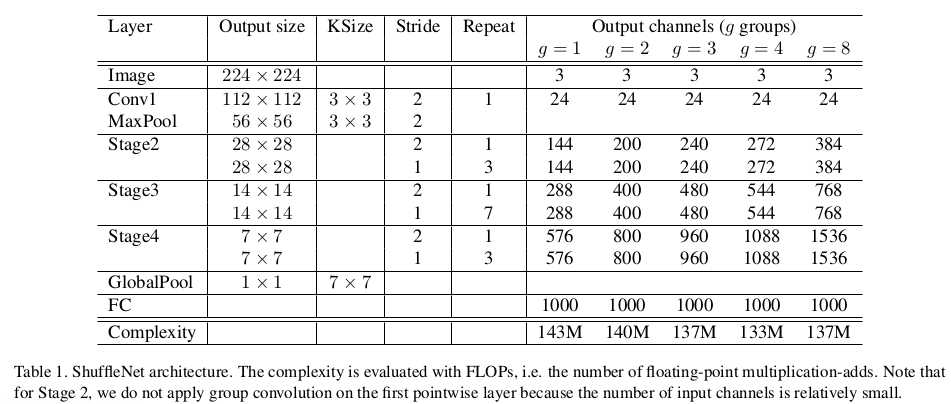
结果比较
论文后面用了种实验证明这两个技术的有效性,且证实了ShuffleNet的优秀,这里就不细说,看论文后面的表就能一目了然。