二分与三分

Posted 2021-01-14 shzr

 

二分与三分

　　(写的很早忘了发布了...)今天高二的学长学姐们进行了二分和三分的测试(又名一本通课后题测试)，感觉这个好有意思~

　　关于什么是二分，三分，先咕咕咕了，来看一道题。

　　灯泡：https://loj.ac/problem/10016

　　

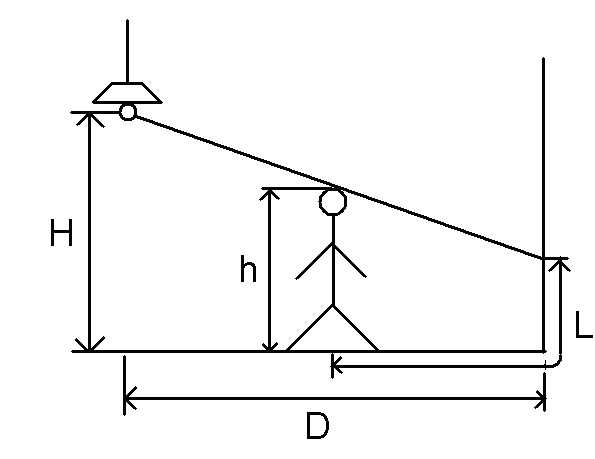
　　题意概述：给出$H,h,D$,求阴影的最长长度(包括地上的和墙上的)。

　　有种初中数学的既视感。

　　解：设灯泡为$A$，人头为$B$，连接$AB$并延长，与地面的延长线交于点$C$.

　　

　　

　　

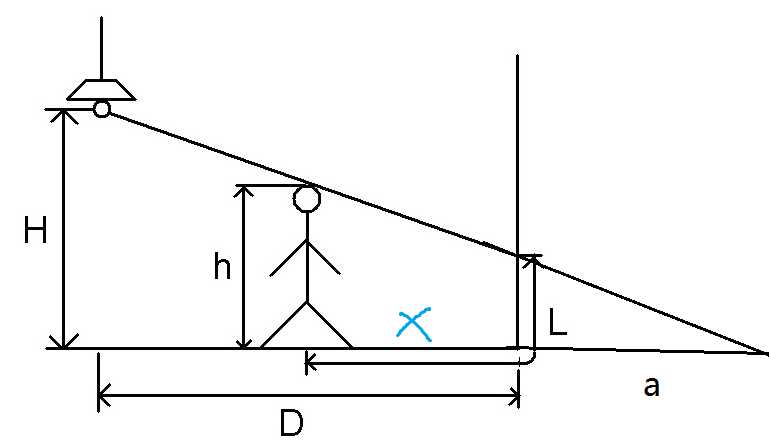
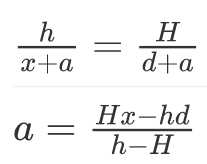
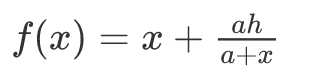
　　于是就结束了...吗？

　　还有一种可能就是影子并没有到墙上去，但是影响不大，两个函数叠加起来还是单峰的，似乎就是那种对勾函数？　

　　

 1 # include <cstdio>
 2 # include <iostream>
 3 
 4 using namespace std;
 5 
 6 int T;
 7 double H,h,d,a1,a2;
 8 double ans,l,r,lmid,rmid;
 9 
10 double f (double x)
11 {
12     double ans=0,a,b;
13     b=h*(d-x)/(H-h);
14     if(b<=x)
15         return b;
16     ans+=x;
17     a=(x*H-d*h)/(h-H);
18     ans+=a*h/(x+a);
19     return ans;
20 }
21 
22 int main()
23 {
24     scanf("%d",&T);
25     while (T--)
26     {
27         scanf("%lf%lf%lf",&H,&h,&d);
28         l=0,r=d,ans=0;
29         while (r-l>=0.0001)
30         {
31             lmid=l+(r-l)/3.0;
32             rmid=r-(r-l)/3.0;
33             a1=f(lmid);
34             a2=f(rmid);
35             if(f(lmid)<f(rmid))
36                 l=lmid;
37             else 
38                 r=rmid;
39         }
40         printf("%.3lf
",f(l));
41     }
42     return 0;
43 }

灯泡

 

　　迎风舞:https://www.cnblogs.com/shzr/p/9751719.html

 

　　传送带:https://www.luogu.org/problemnew/show/P2571

　　题意概述:给定平面上的两条线段,在每条上移动的速度分别是$a$,$b$,也可以脱离线段到平面上走,同样有一个速度$c$,求从第一条线段上的$A$点到另一条上的$D$点的最短距离.

　　首先想到的是贪心...如果平面上走的快就到面上去,如果线上更快就在线上走,然而这个显然是错的,因为有时虽然线上走的快,但是却越走越偏?

　　最终的答案应该是在起始线段上走一段,再在平面上走一段到达终点线段,再在那条线段上一直走到终点.先考虑一个比较简单的问题,如果只是平面上有一条线段,求从某个点到线段端点的最小距离怎么做?列方程发现是一个二次函数,可以求出系数来求极值,也可以三分.现在考虑起始点不固定的情况:如果对于每个起始点都求出最小距离,可以视为一个关于起始点的函数.首先这个函数应该是连续的,所以要是想不明白上模拟退火也行,显然它不一定是单调的,但是应该也不是特别奇怪的形状,严谨的证明其实我也不会,但是可以感受一下.最优解肯定是存在的,而且起始点越偏离最优解答案就越劣.为什么?以下是胡乱证明,不保证正确:起始点移动一点,到达点也会相应的移动一些,在很小的范围内这种移动可能是单调的,但是过了某一个点之后就会往反方向移动?

　　

　　总之网上也没找到好的证明,就这样吧.

　　注意:有可能某一条线段退化成一个点,三分还没开始就退出了...可以考虑换成控制三分次数的做法.

　　

 1 # include <cstdio>
 2 # include <iostream>
 3 # include <cmath>
 4 # include <algorithm>
 5 
 6 using namespace std;
 7 
 8 const int maxn=300;
 9 int ax,ay,bx,by;
10 int cx,cy,dx,dy;
11 double p,q,r;
12 double la,lb,L,R,lmid,rmid;
13 int cnt=maxn;
14 
15 inline double l (double len,double x,double y)
16 {
17     double ans=0,x_,y_;
18     x_=cx,y_=cy;
19     if(lb) x_=len*(dx-cx)/lb+cx;
20     if(lb) y_=len*(dy-cy)/lb+cy;
21     ans+=sqrt((x_-dx)*(x_-dx)+(y_-dy)*(y_-dy))/q;
22     ans+=sqrt((x-x_)*(x-x_)+(y-y_)*(y-y_))/r;
23     return ans;    
24 }
25 
26 inline double f (double len)
27 {
28     double L=0,R=lb,lmid,rmid,x,y,l1;
29     x=ax,y=ay;
30     if(la) x=len*(bx-ax)/la+ax;
31     if(la) y=len*(by-ay)/la+ay;
32     l1=sqrt((x-ax)*(x-ax)+(y-ay)*(y-ay))/p;
33     int cnt=maxn;
34     while (cnt)
35     {
36         lmid=L+(R-L)/3.0;
37         rmid=R-(R-L)/3.0;
38         if(l(lmid,x,y)>l(rmid,x,y))
39             L=lmid;
40         else R=rmid;
41         cnt--;
42     }
43     return l(L,x,y)+l1;
44 }
45 
46 int main()
47 {
48     scanf("%d%d%d%d",&ax,&ay,&bx,&by);
49     scanf("%d%d%d%d",&cx,&cy,&dx,&dy);
50     scanf("%lf%lf%lf",&p,&q,&r);
51     la=sqrt((ax-bx)*(ax-bx)+(ay-by)*(ay-by));
52     lb=sqrt((cx-dx)*(cx-dx)+(cy-dy)*(cy-dy));
53     L=0,R=la;
54     while (cnt)
55     {
56         lmid=L+(R-L)/3.0;
57         rmid=R-(R-L)/3.0;
58         if(f(lmid)>f(rmid))
59             L=lmid;
60         else R=rmid;
61         cnt--;
62     }
63     printf("%.2lf",f(R));
64     return 0;
65 }

传送带

---shzr