骑士共存问题

Posted 2021-01-14 fighting-sh

骑士共存问题

https://www.luogu.org/problemnew/show/P3355

题目描述

在一个 n*n个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍，骑士不得进入

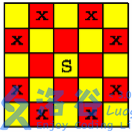
对于给定的 n*n 个方格的国际象棋棋盘和障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击

输入输出格式

输入格式：

 

第一行有 2 个正整数n 和 m (1<=n<=200, 0<=m<n2)，分别表示棋盘的大小和障碍数。接下来的 m 行给出障碍的位置。每行 2 个正整数，表示障碍的方格坐标。

 

输出格式：

 

将计算出的共存骑士数输出

 

输入输出样例

输入样例#1： 

3 2
1 1
3 3

输出样例#1： 

5


把格子黑白染色，利用最小割求解。感觉与方格取数是同一题型

  1 #include<iostream>
  2 #include<cstring>
  3 #include<string>
  4 #include<cmath>
  5 #include<cstdio>
  6 #include<algorithm>
  7 #include<queue>
  8 #include<vector>
  9 #include<set>
 10 #define maxn 100005
 11 #define MAXN 100005
 12 #define mem(a,b) memset(a,b,sizeof(a))
 13 const int N=200005;
 14 const int M=200005;
 15 const int INF=0x3f3f3f3f;
 16 using namespace std;
 17 int n;
 18 struct Edge{
 19     int v,next;
 20     int cap,flow;
 21 }edge[MAXN*20];//注意这里要开的够大。。不然WA在这里真的想骂人。。问题是还不报RE。。
 22 int cur[MAXN],pre[MAXN],gap[MAXN],path[MAXN],dep[MAXN];
 23 int cnt=0;//实际存储总边数
 24 void isap_init()
 25 {
 26     cnt=0;
 27     memset(pre,-1,sizeof(pre));
 28 }
 29 void isap_add(int u,int v,int w)//加边
 30 {
 31     edge[cnt].v=v;
 32     edge[cnt].cap=w;
 33     edge[cnt].flow=0;
 34     edge[cnt].next=pre[u];
 35     pre[u]=cnt++;
 36 }
 37 void add(int u,int v,int w){
 38     isap_add(u,v,w);
 39     isap_add(v,u,0);
 40 }
 41 bool bfs(int s,int t)//其实这个bfs可以融合到下面的迭代里，但是好像是时间要长
 42 {
 43     memset(dep,-1,sizeof(dep));
 44     memset(gap,0,sizeof(gap));
 45     gap[0]=1;
 46     dep[t]=0;
 47     queue<int>q;
 48     while(!q.empty())
 49     q.pop();
 50     q.push(t);//从汇点开始反向建层次图
 51     while(!q.empty())
 52     {
 53         int u=q.front();
 54         q.pop();
 55         for(int i=pre[u];i!=-1;i=edge[i].next)
 56         {
 57             int v=edge[i].v;
 58             if(dep[v]==-1&&edge[i^1].cap>edge[i^1].flow)//注意是从汇点反向bfs，但应该判断正向弧的余量
 59             {
 60                 dep[v]=dep[u]+1;
 61                 gap[dep[v]]++;
 62                 q.push(v);
 63                 //if(v==sp)//感觉这两句优化加了一般没错，但是有的题可能会错，所以还是注释出来，到时候视情况而定
 64                 //break;
 65             }
 66         }
 67     }
 68     return dep[s]!=-1;
 69 }
 70 int isap(int s,int t)
 71 {
 72     if(!bfs(s,t))
 73     return 0;
 74     memcpy(cur,pre,sizeof(pre));
 75     //for(int i=1;i<=n;i++)
 76     //cout<<"cur "<<cur[i]<<endl;
 77     int u=s;
 78     path[u]=-1;
 79     int ans=0;
 80     while(dep[s]<n)//迭代寻找增广路,n为节点数
 81     {
 82         if(u==t)
 83         {
 84             int f=INF;
 85             for(int i=path[u];i!=-1;i=path[edge[i^1].v])//修改找到的增广路
 86                 f=min(f,edge[i].cap-edge[i].flow);
 87             for(int i=path[u];i!=-1;i=path[edge[i^1].v])
 88             {
 89                 edge[i].flow+=f;
 90                 edge[i^1].flow-=f;
 91             }
 92             ans+=f;
 93             u=s;
 94             continue;
 95         }
 96         bool flag=false;
 97         int v;
 98         for(int i=cur[u];i!=-1;i=edge[i].next)
 99         {
100             v=edge[i].v;
101             if(dep[v]+1==dep[u]&&edge[i].cap-edge[i].flow)
102             {
103                 cur[u]=path[v]=i;//当前弧优化
104                 flag=true;
105                 break;
106             }
107         }
108         if(flag)
109         {
110             u=v;
111             continue;
112         }
113         int x=n;
114         if(!(--gap[dep[u]]))return ans;//gap优化
115         for(int i=pre[u];i!=-1;i=edge[i].next)
116         {
117             if(edge[i].cap-edge[i].flow&&dep[edge[i].v]<x)
118             {
119                 x=dep[edge[i].v];
120                 cur[u]=i;//常数优化
121             }
122         }
123         dep[u]=x+1;
124         gap[dep[u]]++;
125         if(u!=s)//当前点没有增广路则后退一个点
126         u=edge[path[u]^1].v;
127      }
128      return ans;
129 }
130 
131 int dir[8][2]={-2,-1,-1,-2,1,2,2,1,-1,2,1,-2,-2,1,2,-1};
132 int map[205][205];
133 
134 int main(){
135     int m,s,t;
136     cin>>n>>m;
137     int a,b,c;
138     int v,u;
139     isap_init();
140     for(int i=1;i<=m;i++){
141         cin>>v>>u;
142         map[v][u]=1;
143     }
144     s=0,t=n*n+1;
145     for(int i=1;i<=n;i++){
146         for(int j=1;j<=n;j++){
147             if(!map[i][j]){
148                 if((i+j)&1){
149                     add(s,(i-1)*n+j,1);
150                     for(int k=0;k<8;k++){
151                         v=i+dir[k][0];
152                         u=j+dir[k][1];
153                         if((v>=1)&&(v<=n)&&(u>=1)&&(u<=n)&&(!map[v][u])){
154                             add((i-1)*n+j,(v-1)*n+u,1);
155                         }
156                     }
157                 }
158                 else{
159                     add((i-1)*n+j,t,1);
160                 }
161             }
162         }
163     }
164     int ans=n*n-m;
165     n=n*n+2;
166     cout<<ans-isap(s,t)<<endl;
167 }

View Code