机器学习决策树

Posted 2021-01-14 bep-feijin

1、决策树简介

1.1 决策树概述

决策树算法是一种基于树形结构的分类算法，它能从给定的无序的训练样本中，提炼出树型的分类模型，树形中包含判断模块和终止模块。它是一种典型的分类算法，首先对数据进行处理，利用归纳算法生成可读的规则和决策树，然后使用决策对新数据进行分析。本质上决策树是通过一系列规则对数据进行分类的过程。决策树是一种监督学习，因此需要提前给出类别标签和数据集合。

决策树的原理：每个决策树都表述了一种树型结构，它由它的分支来对该类型的对象依靠属性进行分类。每个决策树可以依靠对源数据库的分割进行数据测试。这个过程可以递归式的对树进行修剪。 当不能再进行分割或一个单独的类可以被应用于某一分支时，递归过程就完成了。

常用的决策树算法有ID3，C4.5这两种算法本质上是一样的。ID3此算法的目的在于减少树的深度，但是忽略了叶子数目的研究。C4.5算法在ID3的基础上进行了改进，对于预测变量的缺值处理、剪枝技术、派生规则等方面作了较大改进，既适合于分类问题，又适合于回归问题。

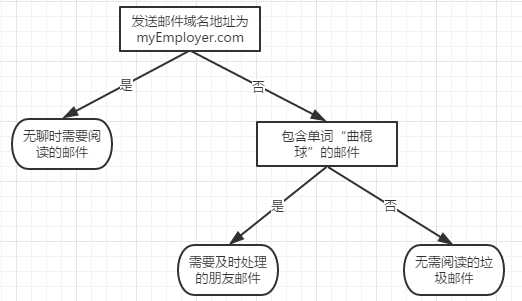
流程图形式的决策树

 

1.2 ID3算法

基本的ID3 算法通过自顶向下构造决策树来进行学习。

构造过程是从“哪一个属性将在树的根结点被测试？”这个问题开始的。

为了回答这个问题，使用统计测试来确定每一个实例属性单独分类训练样例的能力。

（1）分类能力最好的属性被选作树的根结点的测试。

（2）然后为根结点属性的每个可能值产生一个分支，并把训练样例排列到适当的分支（也就是，样例的该属性值对应的分支）之下。

（3）然后重复整个过程，用每个分支结点关联的训练样例来选取在该点被测试的最佳属性。

这形成了对合格决策树的贪婪搜索（greedy search ），也就是算法从不回溯重新考虑以前的选择。

ID3 算法的核心问题是选取在树的每个结点要测试的属性。

我们希望选择的是最有助于分类实例的属性。那么衡量属性价值的一个好的定量标准是什么呢？这里将定义一个统计属性，称为“信息增益（information gain ）”，用来衡量给定的属性区分训练样例的能力。ID3算法通过计算每个属性的信息增益，认为信息增益高的是好属性，每次划分选取信息增益最高的属性为划分标准，重复这个过程，直至生成一个能完美分类训练样例的决策树。

1.3 信息增益

 划分数据集的原则就是将无序的数据变得更加有序，组织数据的一种方式就是用信息论度量信息。

在划分数据集之前和之后信息所发生的变化称为信息增益。通过计算每个特征值划分数据集获得的信息增益，获得信息增益最高的特征就是最好的选择。

熵(entropy)：度量随机变量的不确定性。

定义：假设随机变量X的可能取值有x_1，x₂， ... , x_n，对于每一个可能的取值x_i，其概率 P(X=x_i) = p_i , ( i = 1,2, ... , n)

因此随机变量X的熵：

 ({H=-sum_{n}^{i=1}p(x_{i})log_{2}p(x_{i})})

 推广到样本集合D，随机变量X是样本的类别，即，假设样本有K个类别，每个类别的概率是，其中|C_k|表示类别k的样本个数，|D|表示样本总数

则对于样本集合D来说熵（经验熵）为：

(H(D)=-sum_{k=1}^{K}frac{left | C_{_{k}} ight |}{left | D ight |}log_{2}frac{left | C_{_{k}} ight |}{left | D ight |})

 对信息增益的理解：对于待划分的数据集D，其 entroy(前)是一定的，但是划分之后的熵 entroy(后)是不定的，entroy(后)越小说明使用此特征划分得到的子集的不确定性越小（也就是纯度越高），因此 entroy(前) -  entroy(后)差异越大，说明使用当前特征划分数据集D的话，其纯度上升的更快。而我们在构建最优的决策树的时候总希望能更快速到达纯度更高的集合，这一点可以参考优化算法中的梯度下降算法，每一步沿着负梯度方法最小化损失函数的原因就是负梯度方向是函数值减小最快的方向。同理：在决策树构建的过程中我们总是希望集合往最快到达纯度更高的子集合方向发展，因此我们总是选择使得信息增益最大的特征来划分当前数据集D。

#计算给定数据集的熵
from math import log

def calcShannonEnt (dataSet):
    numEntroiese = len(dataSet)
    labelCounts = {}
    #为所有可能的分类创建字典，
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key]) / numEntroiese
        shannonEnt -=prob * log(prob,2)
    return shannonEnt