10.22校内测试二分二分图很像莫队的乱搞/树状数组

Posted 2021-01-14 wans-caesar-02111007

Solution

谁能想到这道题卡读入？？还卡了70pts？？？

二分+$n^2$check就行了

Code

#include<bits/stdc++.h>
using namespace std;

int n, m;
int sum[2005][2005];

void read(int &x) {
    x = 0; char ch = getchar();
    while(ch > ‘9‘ || ch < ‘0‘)    ch = getchar();
    while(ch >= ‘0‘ && ch <= ‘9‘) {
        x = x * 10 + ch - ‘0‘;
        ch = getchar();
    }
}

bool check(int mid) {
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++) {
            int x = i - mid, y = j - mid;
            if(x < 0 || y < 0)    continue;
            int tmp = sum[i][j] - sum[x][j] - sum[i][y] + sum[x][y];
            if(tmp == mid * mid)    return 1;
        }
    return 0;
}

int erfen() {
    int ans = 0, l = 0, r = min(n, m);
    while(l <= r) {
        int mid = (l + r) >> 1;
        if(check(mid))    ans = mid, l = mid + 1;
        else    r = mid - 1;
    }
    return ans;
}

int main() {
    freopen("inspect.in", "r", stdin);
    freopen("inspect.out", "w", stdout);
    read(n); read(m);
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= m; j ++) {
            int a;
            read(a);
            sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a;
        }
    int ans = erfen();
    printf("%d", ans);
    return 0;
}

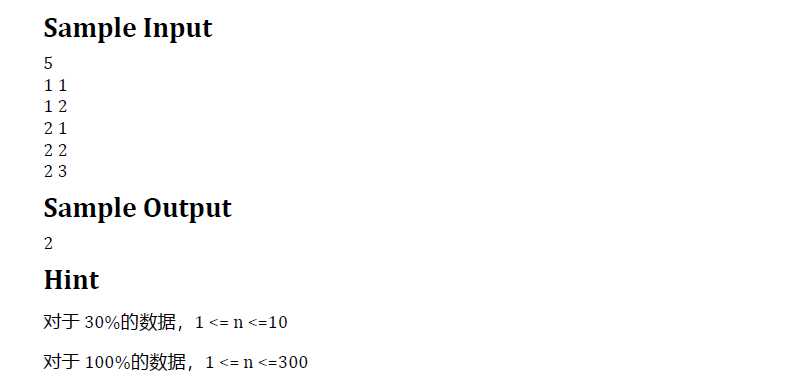
Solution

谁能想到这道题标程错误？？又卡了70pts！

正解二分图/网络流，就是最小路径覆盖问题。

标程错在没判重！

(我判了哼

Code

#include<bits/stdc++.h>
using namespace std;

struct QAQ {
    int x, y;
} book[305], a[305];
bool cmp(QAQ a, QAQ b) { if(a.y == b.y)    return a.x > b.x;    return a.y > b.y; }

struct Node {
    int v, nex;
    Node(int v = 0, int nex = 0) :
        v(v), nex(nex) { }
} Edge[90005];

int stot, h[1005];
void add(int u, int v) {
    Edge[++stot] = Node(v, h[u]);
    h[u] = stot;
}

bool check(int i, int j) {
    if(book[i].x >= book[j].x && book[i].y >= book[j].y)    return 1;
    return 0;
}

int vis[1005], to[1005], pi[1005];
bool dfs(int u) {
    for(int i = h[u]; i; i = Edge[i].nex) {
        int v = Edge[i].v;
        if(!vis[v]) {
            vis[v] = 1;
            if(!to[v] || dfs(to[v])) {
                to[v] = u;
                pi[u] = v;
                return 1;
            }
        }
    }
    return 0;
}

int n;
int main() {
    freopen("militarytraining.in", "r", stdin);
    freopen("militarytraining.out", "w", stdout);
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++) {
        scanf("%d%d", &book[i].x, &book[i].y);
    }
    sort(book + 1, book + 1 + n, cmp);
    for(int i = 1; i <= n; i ++)
        for(int j = i + 1; j <= n; j ++) {
            if(check(i, j))
                add(i, j + n);
        }
    int ans = 0;
    for(int i = 1; i <= n; i ++) {
        if(!pi[i]) {
            memset(vis, 0, sizeof(vis));
            ans += dfs(i);
        }
    }
    printf("%d", n - ans);
    return 0;
}

Solution

今天唯一一道有水平并且T得心甘情愿的题！

卡莫队啊~

所以就乱搞了QAQ

很容易知道满足条件的数k一定不超过O(sqrt(n))个，所以对于70%的数据可以暴力统计有哪些数出现次数超过它本身，之后每次询问查询这些数有多少在该区间内满足要求。（可以用多一个sqrt(n)的空间复杂度换取询问少一个log）

但对于100%的数据，显然不是超时就是炸空间。

考虑将询问按左端点排序，从右向左做。（然而我（zyl dalao！）从左往右）

维护一个数组t，t[i]表示如果询问区间包含了点i，答案会增加t[i]（可能为负）。

初始情况下t全为0，i从n枚举到1，对某个i，考虑a[i]这个数在i位置及其以后是否出现过a[i]次及以上，假设a[i]在位置x出现了第a[i]次，在位置y出现了第a[i]+1次，即表示对于左端点为i的询问区间，当右端点在[x,y)时，a[i]会贡献1的答案，否则贡献0的答案，此时设t[x]=1且t[y]=-1即可。

用一个树状数组维护t数组，可以很容易的统计前缀和。

复杂度为O(nlogn+qlogn+qlogq）。

Code

#include<bits/stdc++.h>
using namespace std;

int n, q, a[1000005];
int pre[1000005], cnt[1000005];

void read(int &x) {
    x = 0; char ch = getchar();
    while(ch > ‘9‘ || ch < ‘0‘)    ch = getchar();
    while(ch >= ‘0‘ && ch <= ‘9‘) {
        x = x * 10 + ch - ‘0‘;
        ch = getchar();
    }
}

struct Node {
    int l, r, ans, id;
} qus[1000005];
bool cmp(Node a, Node b) { return a.l < b.l; }
bool cmp2(Node a, Node b) { return a.id < b.id; }

int lowbit(int x) {
    return x & -x;
}

void add(int pos, int d) {
    for(int i = pos; i <= n; i += lowbit(i))
        pre[i] += d;
}

int query(int pos) {
    int ans = 0;
    for(int i = pos; i; i -= lowbit(i))
        ans += pre[i];
    return ans;
}

void modify(int l, int r, int d) {
    if(r < l)    return ;
    add(l, d);    add(r + 1, -d);
}

int t[1000005], st[1000005], nex[1000005], las[1000005];
void init(int x) {
    if(cnt[x] < x)    return ;
    t[x] = st[x];
    for(int i = 1; i < x; i ++)
        t[x] = nex[t[x]];
    modify(t[x], nex[t[x]] - 1, 1);
}

void change(int x) {
    if(cnt[x] < x)    return ;
    modify(t[x], nex[t[x]] - 1, -1);
    t[x] = nex[t[x]];
    if(t[x] == n + 1) {
        cnt[x] = -1;    return ;
    }
    modify(t[x], nex[t[x]] - 1, 1);
}

int main() {
    freopen("count.in", "r", stdin);
    freopen("count.out", "w", stdout);
    scanf("%d%d", &n, &q);
    for(int i = 1; i <= n; i ++) {
        read(a[i]);
        if(!las[a[i]]) st[a[i]] = i;
        nex[las[a[i]]] = i;
        nex[i] = n + 1;
        las[a[i]] = i;
        cnt[a[i]] ++;
    }
    for(int i = 1; i <= q; i ++)
        read(qus[i].l), read(qus[i].r), qus[i].id = i;
    sort(qus + 1, qus + 1 + q, cmp);
    for(int i = 1; i <= n; i ++)    init(i);
    int L = 1;
    for(int i = 1; i <= q; i ++) {
        while(L < qus[i].l) {
            change(a[L]);
            L ++;
        }
        qus[i].ans = query(qus[i].r);
    }
    sort(qus + 1, qus + 1 + q, cmp2);
    for(int i = 1; i <= q; i ++)    printf("%d
", qus[i].ans);
    return 0;
}

---

 

分手快乐日！ 祝我和自己百年好合！