痛苦的 01 矩阵（和式推导）

Posted 2021-01-13 czsharecode

【传送门】https://acm.ecnu.edu.cn/contest/113/problem/C/

 

【题解】

 

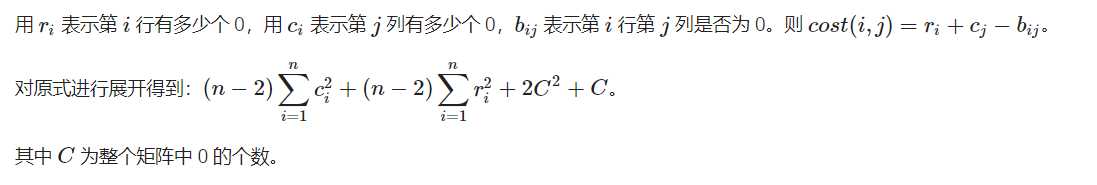
 推导过程：

 

 

【技巧】

（1）直接用二维数组存储矩阵肯定超内存，注意到K的范围该矩阵是一个稀疏的矩阵所以直接将其转化为线性的，a[(i-1)+j]表示其第i行第j列的状况

（2）注意到单个点的改动只能影响到十字形的局部，所以在每次求ans时可以利用上一次的ans加上这一次改动形成的差值（或者说叫贡献）。

（3）一定要注意和式变换时无关项∑别轻易丢弃，也许它形成一个常数n的系数。

 

【AC代码】

#include<iostream>
#include<map>
#include<cstring>
using namespace std;
typedef long long ll;
const int maxn = 2e5+10;
const ll mod = 1e9+7;
ll c[maxn];
ll r[maxn];
ll total;
map<ll,int> mp;
ll n,k,q;

int main(){
    ios::sync_with_stdio(false);
    while(cin>>n>>k>>q){
        ll ans = 0;
        total = n*n - k;//0的总数等于总数减去1的个数
         
        for(int i=1; i<=n; i++){
            c[i] = r[i] = n;
        } 
        mp.clear();
        
        int u, v;
        for(int i=1; i<=k; i++){
            cin>>u>>v;
            mp[(u-1)*n + v] = 1;
            r[u]--;//把1的个数全部减掉就是这一行的0的个数 
            c[v]--;
        }
        for(int i=1; i<=n; i++){
            ans+=r[i]*r[i] % mod;
            ans+=c[i]*c[i] % mod;
        }
        ans = ans % mod;
        ans = (n-2)*ans % mod;
        total = total%mod;
        ans += (2*total*total%mod + total) % mod;
        ans = ans%mod;
        cout<<ans<<endl;//第一次的ans 
        
        for(int i=1; i<=q; i++){
            cin>>u>>v;
            if(mp[(u-1)*n + v]){//如果这一位是1，则反转为0,  0的个数增加 
                mp[(u-1)*n + v] = 0;
                
                ans = ( (ans + (n-2)*(2*r[u] + 2 + 2*c[v]) ) % mod + (4*total + 3) % mod ) % mod;
                
                r[u]++;
                c[v]++;
                total++;
                
            }
            else{
                mp[(u-1)*n + v] = 1;
                ans = ( (ans + (n-2)*(-2*r[u] + 2 - 2*c[v]) + mod) % mod + (-4*total + 1) % mod ) % mod;
                ans = (ans + mod)%mod;//防止ans是负数 
                r[u]--;
                c[v]--;
                total--;
            }
            cout<<ans<<endl;
        }
    }
}