[HAOI2009]毛毛虫

Posted 2021-01-13 aptx--4869

题意描述

思路

[HAOI2009]毛毛虫
树形DP
最大毛毛虫可以看做以一个节点为根
求它子树中节点及直接相邻节点个数最多的两条链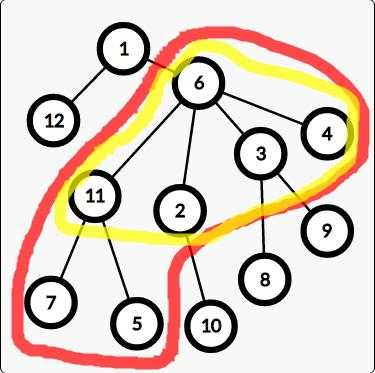
用con[now]数组表示i的子树中跟i直接相连的点的个数
(代码中的con[now]包括now自身)
假设 树根now=6,如图黄色部分
用num[now]表示以now为根的子树的链上及直接相连的点的最大个数
假设 树根now=6,如图红色部分
注“链上点及与其直接相邻的点最多的链”在此简称“最长链”
num的转移可写作：num[now]=max(num[now],num[v]+con[now]-1)
我们最终要求的是两条链，就相当于就最长链和次长链
在这里没有必要再循环一次来寻找次长链
可以直接设全局变量answer来记录“num[i]更新前的最长链+i子树中的最长链”的最大值
更新：answer=max(answer,num[u]+num[v]-1)
-1是因为v点重复
但是需要注意，如果答案中两条链的根节点不是1,
那么这个毛毛虫还包括根节点的父亲节点
如果根节点恰好是1，就没有所谓“父亲节点”
所以要进行判断
设select[i]=true表示根节点是i
最终进行判断即可

#include<iostream>
#include<cstring>
#include<cstdio>
#define N 300005
using namespace std;
int n,m;
struct edge{
    int u,v,nxt;
}e[N*2];
int cnt,first[N];
void add_edge(int x,int y){
    e[++cnt].u=x;
    e[cnt].v=y;
    e[cnt].nxt=first[x];
    first[x]=cnt;
}
bool vis[N];
int num[N],con[N];
void dfs(int now,int fat){
    vis[now]=true;
    for(int i=first[now];i;i=e[i].nxt){
        int v=e[i].v;
        if(!vis[v]){
            dfs(v,now);
            con[now]++;
        }
    }
}
int answer;
bool select[N];
void dp(int now){
    num[now]=con[now];
    vis[now]=true;
    for(int i=first[now];i;i=e[i].nxt){
        int v=e[i].v;
        if(!vis[v]){
            dp(v);
            if(answer<num[now]+num[v]-1){
                answer=num[now]+num[v]-1;
                select[now]=true;
            }
//            answer=max(answer,num[u]+num[v]-1);
            num[now]=max(num[now],num[v]+con[now]-1);
        }
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) con[i]=1;
    for(int i=1;i<=m;i++){
        int x,y;scanf("%d%d",&x,&y);
        add_edge(x,y);
        add_edge(y,x);
    }
    dfs(1,0);
//    for(int i=1;i<=n;i++){
//        printf("%d: %d %d
",i,con[i],num[i]);
//    }
    memset(vis,false,sizeof(vis));
    dp(1);
    if(!select[1]) answer++;
    printf("%d
",answer);
    return 0;
}