hdu-1540线段树刷题

Posted 2021-01-13 31415926535x

---

title: hdu-1540线段树刷题
date: 2018-10-18 19:55:21
tags:

• acm
• 刷题
  categories:

• ACM-线段树

概述

哇，，，这道线段树的题可以说是到目前为止我所做过的最难的一道了吧QAQ，，，，，，

一开始读完题就是一脸懵逼，，，，完全不知道该从哪里下手，，，就是知道这是一道线段树的题也不知道该怎么下手啊啊啊，，，，

最后还是看了kaungbin大佬的代码，，，QAQ

光是读代码就花了一两个小时，，，（不过也有可能和今天贼困有关，，，脑袋不怎么转啊

分析思路

题意

大概的题意就是一串在一条线上的村庄，，或者说是点，，，一开始都为1，，，然后有三种不同的操作，，，

• d a: 意味着将a这个点置为0，，，
• q a: 意味着询问a周围有多少的1，，，只要碰到零就不算了，，，例如110111110,,(q 5) = 5
• r: 意味着将上一个被置为零的点置为1

分析

我的想法

一开始我看到有需要上一次操作的情况，，就想着要将这些d操作保存下来，，适合这道题的就是栈，，，

然后就是询问了，，，我那时想着既然要求a周围这些1的个数，，那我就找到两端的0不就行了，，，然后从这里就彻底的脑抽了，，，又想着用线段树去求这段区间的和，，，，然后结果显而易见，，，，t了，，，

因为，，这种想法线段树根本没有用啊！！！！都找出那两端的0所在的位置直接减不就行了，，，这不就是裸暴力吗，，，，，哇，，，被自己蠢哭(?????????)，，，，

斌神的做法

首先将这段线划分成多个区段，，，每个区段保存的信息有：从这去区段的左端点开始最长的连续1的个数ll 、 从这个区段右端点开始的最长的连续1的个数rl 、 还有这个区段最大的连续点的个数ml。。。

建树：ll = rl = ml = 区间长

更新：

叶子节点置一置零，，，

左右递归更新

其他区间：(pushup())
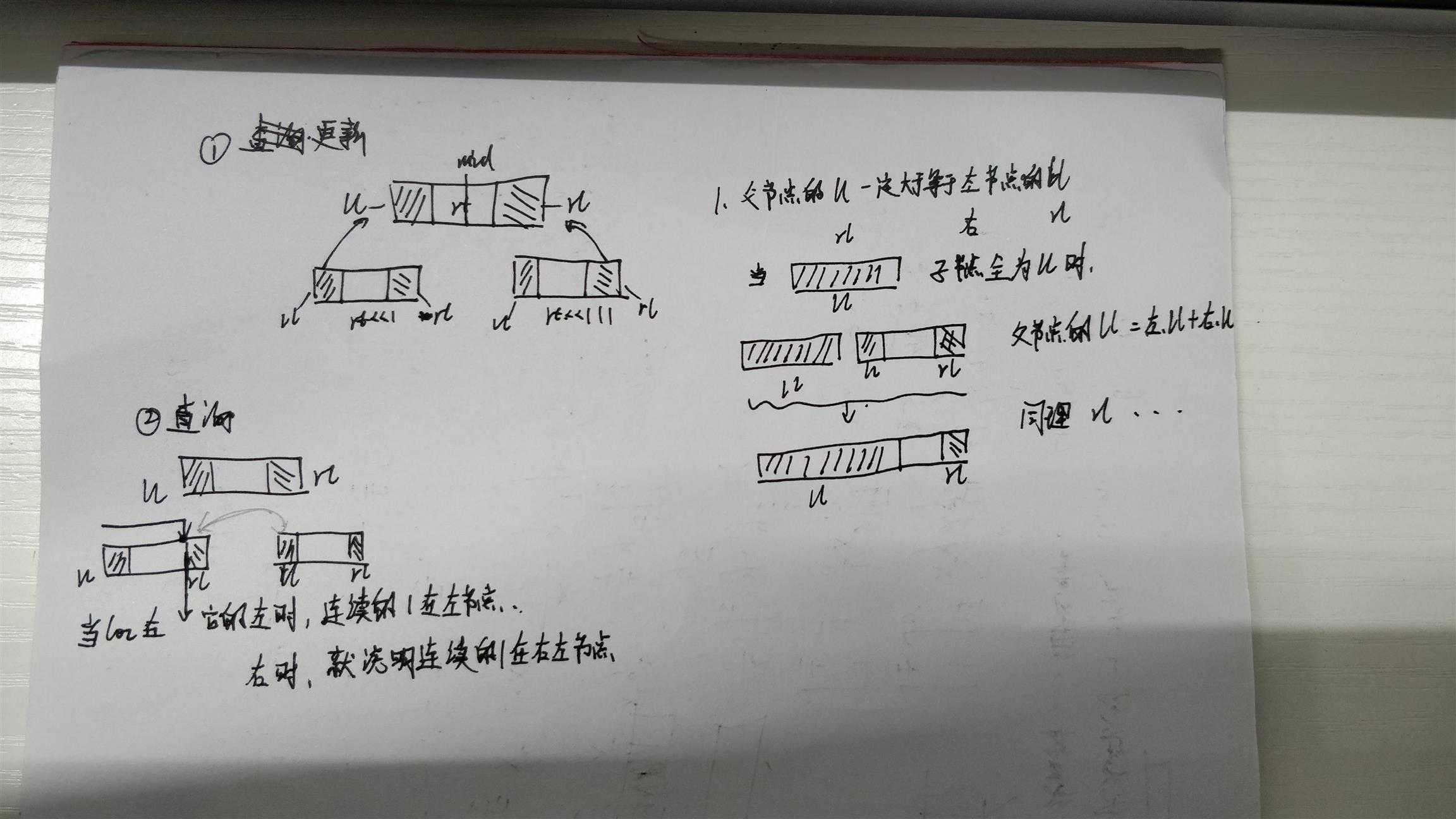
父节点.ll = 左节点.ll 父节点.rl = 右节点.rl
父节点.ml取左右节点的最大的一个ml
若左节点的rl + 右节点的ll > 父节点的ml，，，，就更新为前者

对于父节点的ll,rl
如果左节点的ll为左节点的长度，，，就说明左节点从左端点开始的连续1的最大的个数就为左节点包含的点的个数，，，所以此时的父节点的ll就要和右节点的ll合并
同理，，，父节点的rl也要进行这样的判断

查询：

对于一些特殊的区间直接返回该区间的最大的连续1的个数也就是ml

当loc在中点左时，，，就要从左节点来判断，，，判断的条件是loc是否超出了rl的最左端（画图更容易理解一些），，，超出的话就说明loc所在的连续的1一部分是在左节点的rl里另一部分是在右节点的ll里，，，就分成两个点查询，，，一个是在左节点的loc，，，另一个时在右节点的mid+1那个点
同理，，若在中点的右时也有类似的判断，，，
大体上说就是不断地判断要找到那个点相对ll,rl的位置，，，最后把递归查询到的结果合并就行了，，，

字丑见谅，，，，（不过应该没人看把，，，，

代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>

using namespace std;

const int maxn = 5e5 + 10;

struct node
{
    int l;
    int r;
    int ml;
    int ll;
    int rl;
}node[maxn << 2];

void build(int rt , int l , int r)
{
    node[rt].l = l;
    node[rt].r = r;
    node[rt].ml = node[rt].ll = node[rt].rl = r - l + 1;    //刚开始肯定是区间的长度
    if(l == r) return;
    int mid = (l + r) >> 1;
    build(rt << 1 , l , mid);
    build(rt << 1 | 1 , mid + 1 , r);
    return;
}
void update(int rt , int loc , int val)
{
    if(node[rt].l == node[rt].r)
    {
        if(val) node[rt].ml = node[rt].ll = node[rt].rl = 1;    //摧毁和重建两种
        else    node[rt].ml = node[rt].ll = node[rt].rl = 0;
        return;
    }
    int mid = (node[rt].l + node[rt].r) >> 1;
    if(loc <= mid)  update(rt << 1 , loc , val);
    else            update(rt << 1 | 1 , loc , val);
    //递归更新
    //先更新父节点的两个，ll,rl
    node[rt].ll = node[rt << 1].ll;
    node[rt].rl = node[rt << 1 | 1].rl;

    //然后是父节点的ml
    node[rt].ml = max(node[rt << 1].ml , node[rt << 1 | 1].ml);
    node[rt].ml = max(node[rt].ml , node[rt << 1].rl + node[rt << 1 | 1].ll);

    //父节点的ll,rl可能就是左右节点的ll,,rl,,,,当刚好是子节点的全部时还要加上另一个区间的一部分
    if(node[rt << 1].ll == node[rt << 1].r - node[rt << 1].l + 1)
        node[rt].ll += node[rt << 1 | 1].ll;
    if(node[rt << 1 | 1].rl == node[rt << 1 | 1].r - node[rt << 1 | 1].l + 1)
        node[rt].rl += node[rt << 1].rl;
    return;
}
int query(int rt , int loc)
{
    //特殊情况直接返回ml
    if(node[rt].l == node[rt].r || node[rt].ml == 0 || node[rt].ml == node[rt].r - node[rt].l + 1)
        return node[rt].ml;

    int mid = (node[rt].l + node[rt].r) >> 1;
    if(loc <= mid)
    {
        if(loc >= node[rt << 1].r - node[rt << 1].rl + 1)
            return query(rt << 1 , loc) + query(rt << 1 | 1 , mid + 1);
        else
            return query(rt << 1 , loc);
    }
    else
    {
        if(loc <= node[rt << 1 | 1].l + node[rt << 1 | 1].ll - 1)
            return query(rt << 1 | 1 , loc) + query(rt << 1 , mid);
        return query(rt << 1 | 1 , loc);
    }
}
int main()
{
    int n , m;
    while(scanf("%d%d" , &n , &m) != EOF)
    {
        build(1 , 1 , n);
        int q[maxn];
        int toc = 0;
        int t = 0;
        while(m--)
        {
            char c;scanf(" %c" , &c);
            if(c == 'D')
            {
                scanf("%d" , &t);
                q[toc++] = t;   //把摧毁操作保存
                update(1 , t , 0);
            }
            else if(c == 'Q')
            {
                scanf("%d" , &t);
                printf("%d
" , query(1 , t));
            }
            else
            {
                if(t)
                {
                    t = q[--toc];
                    update(1 , t , 1);
                }
            }
        }
    }
    return 0;
}
//kaungbin